Tension superficielle
La tension superficielle est un effet où la surface d'un liquide est forte. La surface peut supporter un poids, et la surface d'une goutte d'eau maintient la goutte ensemble, en forme de boule. Certaines petites choses peuvent flotter sur une surface à cause de la tension superficielle, même si normalement elles ne pourraient pas flotter. Certains insectes (par exemple les piétinements) peuvent ainsi courir à la surface de l'eau. Cette propriété est due au fait que les molécules du liquide sont attirées les unes vers les autres (cohésion), et est responsable de nombreux comportements des liquides.
La tension superficielle a la dimension de la force par unité de longueur, ou de l'énergie par unité de surface. Les deux sont équivalentes, mais lorsqu'on parle d'énergie par unité de surface, on utilise le terme d'énergie de surface, qui est plus général dans le sens où il s'applique aussi aux solides et pas seulement aux liquides.
En science des matériaux, la tension superficielle est utilisée soit pour la contrainte de surface, soit pour l'énergie libre de surface.
Causes
Les forces de cohésion entre les molécules liquides provoquent une tension de surface. Dans la majeure partie du liquide, chaque molécule est tirée de manière égale dans toutes les directions par les molécules liquides voisines, ce qui donne une force nette de zéro. Les molécules à la surface n'ont pas d'autres molécules de tous les côtés et sont donc attirées vers l'intérieur. Cela crée une certaine pression interne et force les surfaces liquides à se contracter à la surface minimale.
La tension superficielle est responsable de la forme des gouttelettes de liquide. Bien que facilement déformables, les gouttelettes d'eau ont tendance à prendre une forme sphérique sous l'effet des forces de cohésion de la couche superficielle. En l'absence d'autres forces, y compris la gravité, les gouttes de pratiquement tous les liquides seraient parfaitement sphériques. La forme sphérique minimise la "tension de paroi" nécessaire de la couche de surface selon la loi de Laplace.
Une autre façon de l'envisager est en termes d'énergie. Une molécule en contact avec un voisin est dans un état d'énergie plus faible que si elle était seule (pas en contact avec un voisin). Les molécules intérieures ont autant de voisins qu'elles peuvent en avoir, mais les molécules de frontière sont des voisins manquants (par rapport aux molécules intérieures). Ainsi, les molécules limites ont une énergie plus élevée. Pour que le liquide puisse minimiser son état énergétique, le nombre de molécules limites à haute énergie doit être réduit au minimum. La quantité minimisée de molécules limites se traduit par une surface minimisée.
Grâce à la réduction de la surface, une surface prendra la forme la plus lisse possible. Toute courbure de la forme de la surface se traduit par une plus grande surface et une énergie plus élevée. Ainsi, la surface va repousser toute courbure de la même manière qu'une balle poussée vers le haut va repousser pour minimiser son énergie potentielle gravitationnelle.
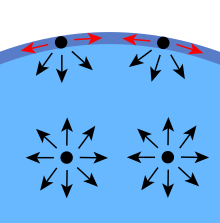
Diagramme des forces exercées sur les molécules dans un liquide

La tension de surface empêche le trombone de s'immerger.
Effets dans la vie quotidienne
Eau
L'étude de l'eau montre plusieurs effets de la tension superficielle :
A. L'eau de pluie forme des perles à la surface d'une surface cireuse, telle qu'une feuille. L'eau adhère faiblement à la cire et fortement à elle-même, de sorte que l'eau se regroupe en gouttes. La tension superficielle leur donne leur forme quasi sphérique, car une sphère a le plus petit rapport surface/volume possible.
B. La formation de gouttes se produit lorsqu'une masse de liquide est étirée. L'animation montre que l'eau qui adhère au robinet prend de la masse jusqu'à ce qu'elle soit étirée à un point où la tension de surface ne peut plus la lier au robinet. Elle se sépare alors et la tension superficielle forme la goutte en une sphère. Si un courant d'eau coulait du robinet, le courant se briserait en gouttes pendant sa chute. La gravité étire le courant, puis la tension superficielle le pince en sphères.
C. Les objets plus denses que l'eau flottent encore lorsque l'objet n'est pas mouillable et que son poids est suffisamment faible pour être supporté par les forces résultant de la tension superficielle. Par exemple, les piétons aquatiques utilisent la tension de surface pour marcher sur la surface d'un étang. La surface de l'eau se comporte comme un film élastique : les pattes de l'insecte provoquent des indentations à la surface de l'eau, ce qui augmente sa surface.
D. La séparation de l'huile et de l'eau (dans ce cas, l'eau et la cire liquide) est causée par une tension de surface entre des liquides différents. Ce type de tension superficielle est appelé "tension d'interface", mais sa physique est la même.
E. Les larmes de vin sont la formation de gouttes et de ruisseaux sur le côté d'un verre contenant une boisson alcoolisée. Sa cause est une interaction complexe entre les différentes tensions superficielles de l'eau et de l'éthanol. Elle est induite par une combinaison de la modification de la tension superficielle de l'eau par l'éthanol, l'éthanol s'évaporant plus rapidement que l'eau.
· 
A. Perlage d'eau sur une feuille
· 
B. L'eau qui s'écoule d'un robinet
· 
C. Les stridents d'eau restent au-dessus du liquide en raison de la tension superficielle
· 
D. Lampe à lave avec interaction entre des liquides différents ; eau et cire liquide
· 
E. Photo montrant le phénomène des "larmes de vin".
Tensioactifs
La tension de surface est visible dans d'autres phénomènes courants, notamment lorsque des agents de surface sont utilisés pour la diminuer :
- Les bulles de savon ont une très grande surface et une très faible masse. Les bulles dans l'eau pure sont instables. L'ajout de tensioactifs peut cependant avoir un effet stabilisateur sur les bulles (voir l'effet Marangoni). Remarquez que les tensioactifs réduisent en fait la tension superficielle de l'eau par un facteur de trois ou plus.
- Les émulsions sont un type de solution dans laquelle la tension de surface joue un rôle. De minuscules fragments d'huile en suspension dans de l'eau pure s'assemblent spontanément en des masses beaucoup plus importantes. Mais la présence d'un agent tensioactif entraîne une diminution de la tension superficielle, ce qui permet de stabiliser les minuscules gouttelettes d'huile dans la masse d'eau (ou vice versa).
Physique de base
Deux définitions
La tension superficielle, représentée par le symbole γ est définie comme la force le long d'une ligne de longueur unitaire, où la force est parallèle à la surface mais perpendiculaire à la ligne. Une façon d'illustrer ce phénomène est d'imaginer un film de savon plat délimité sur un côté par un fil tendu de longueur L. Le fil sera tiré vers l'intérieur du film par une force égale à 2 γ {\displaystyle \scriptstyle \gamma }
Une définition équivalente, utile en thermodynamique, est le travail effectué par unité de surface. Ainsi, pour augmenter la surface d'une masse de liquide d'une certaine quantité, δA, une quantité de travail, γ {\displaystyle \scriptstyle \gamma }
L'équivalence de la mesure de l'énergie par unité de surface à la force par unité de longueur peut être prouvée par une analyse dimensionnelle.
Courbure et pression de la surface
Si aucune force n'agit normalement sur une surface tendue, la surface doit rester plane. Mais si la pression sur un côté de la surface diffère de la pression sur l'autre côté, la différence de pression multipliée par la surface donne une force normale. Pour que les forces de tension superficielle annulent la force due à la pression, la surface doit être courbée. Le diagramme montre comment la courbure d'une minuscule surface conduit à une composante nette des forces de tension superficielle agissant normalement au centre de la surface. Lorsque toutes les forces sont équilibrées, l'équation résultante est connue sous le nom d'équation de Young-Laplace :
Δ p = γ ( 1 R x + 1 R y ) {\displaystyle \Delta p\ =\ \ \gamma \left({\frac {1}{R_{x}}}+{\frac {1}{R_{y}}}\right)}
où :
· Δp est la différence de pression.
· γ {\displaystyle \scriptstyle \gamma }
· Rx et Ry sont des rayons de courbure dans chacun des axes qui sont parallèles à la surface.
La quantité entre parenthèses sur le côté droit est en fait (deux fois) la courbure moyenne de la surface (selon la normalisation).
Les solutions à cette équation déterminent la forme des gouttes d'eau, des flaques, des ménisques, des bulles de savon et de toutes les autres formes déterminées par la tension de surface. (Un autre exemple est la forme des impressions que font les pieds d'un promeneur sur l'eau à la surface d'un étang).
Le tableau ci-dessous montre comment la pression interne d'une goutte d'eau augmente avec un rayon décroissant. Pour les gouttes de petite taille, l'effet est subtil, mais la différence de pression devient énorme lorsque la taille des gouttes se rapproche de la taille moléculaire. (À la limite d'une seule molécule, le concept devient dénué de sens).
| Δp pour les gouttes d'eau de différents rayons à STP | ||||
| Rayon des gouttelettes | 1 mm | 0,1 mm | 1 μm | 10 nm |
| Δp (atm) | 0.0014 | 0.0144 | 1.436 | 143.6 |
Surface liquide
Il est difficile de trouver la forme de la surface minimale délimitée par un cadre de forme arbitraire en utilisant seulement les mathématiques. Pourtant, en façonnant le cadre en fil de fer et en le trempant dans une solution savonneuse, une surface minimale locale apparaîtra en quelques secondes dans le film de savon qui en résulte.
La raison en est que la différence de pression à travers une interface fluide est proportionnelle à la courbure moyenne, comme le montre l'équation de Young-Laplace. Pour un film de savon ouvert, la différence de pression est nulle, donc la courbure moyenne est nulle, et les surfaces minimales ont la propriété d'une courbure moyenne nulle.
Angles de contact
La surface de tout liquide est une interface entre ce liquide et un autre milieu. La surface supérieure d'un étang, par exemple, est une interface entre l'eau de l'étang et l'air. La tension superficielle n'est donc pas une propriété du liquide seul, mais une propriété de l'interface du liquide avec un autre milieu. Si un liquide se trouve dans un récipient, il y a non seulement l'interface liquide/air à sa surface supérieure, mais aussi une interface entre le liquide et les parois du récipient. La tension superficielle entre le liquide et l'air est généralement différente (supérieure) de sa tension superficielle avec les parois d'un récipient. Lorsque les deux surfaces se rencontrent, la géométrie équilibre toutes les forces.
Lorsque les deux surfaces se rencontrent, elles forment un angle de contact, θ {\displaystyle \scriptstyle \theta }


γ l a > γ l s - γ s a > 0 {\displaystyle \gamma _{\mathrm {la} >\ \gamma _{\mathrm {ls} }-\gamma _{\mathrm {sa} }\ >\ 0}
Dans le diagramme, les forces verticales et horizontales doivent s'annuler exactement au point de contact, appelé équilibre. La composante horizontale de f l a {\displaystyle \scriptstyle f_{\mathrm {la} }}

f A = f l a sin θ {\displaystyle f_{\mathrm {A} }\ =\ f_{\mathrm {la} }\sin \theta
Le plus important équilibre des forces, cependant, est dans la direction verticale. La composante verticale de f l a {\displaystyle \scriptstyle f_{\mathrm {la} }}

f l s - f s a = - f l a cos θ {\displaystyle f_{\mathrm {ls} }-f_{\mathrm {sa} }\ =\ -f_{\mathrm {la} }\cos \theta
| Liquid | Solide | Angle de contact | |||
| eau |
| 0° | |||
| éthanol | |||||
| éther diéthylique | |||||
| tétrachlorure de carbone | |||||
| glycérol | |||||
| acide acétique | |||||
| eau | cire de paraffine | 107° | |||
| argent | 90° | ||||
| iodure de méthyle | verre sodo-calcique | 29° | |||
| verre au plomb | 30° | ||||
| quartz fondu | 33° | ||||
| mercure | verre sodo-calcique | 140° | |||
| Quelques angles de contact liquide-solide | |||||
Comme les forces sont directement proportionnelles à leurs tensions de surface respectives, nous avons également :
γ l s - γ s a = - γ l a cos θ {\displaystyle \gamma _{\mathrm {ls} }-\gamma _{\mathrm {sa} =\ -\gamma _{\mathrm {la} }\cos \theta
où
· γ l s {\displaystyle \scriptstyle \gamma _{\mathrm {ls} }}
· γ l a {\displaystyle \scriptstyle \gamma _{\mathrm {la} }}
· γ s a {\displaystyle \scriptstyle \gamma _{\mathrm {sa} }}
· θ {\displaystyle \scriptstyle \theta }
Cela signifie que bien que la différence entre la tension superficielle liquide-solide et solide-air, γ l s - γ s a {\displaystyle \scriptstyle \gamma _{\mathrm {ls} }-\gamma _{\mathrm {sa} }}


Cette même relation existe dans le diagramme de droite. Mais dans ce cas, nous voyons que, comme l'angle de contact est inférieur à 90°, la différence de tension superficielle liquide-solide/solide air doit être négative :
γ l a > 0 > γ l s - γ s a {\displaystyle \gamma _{\mathrm {la} }\ >\ 0\ >\ \gamma _{\mathrm {ls} }-\gamma _{\mathrm {sa} }}
Angles de contact spéciaux
Observez que dans le cas particulier d'une interface eau-argent où l'angle de contact est égal à 90°, la différence de tension superficielle liquide-solide/solide air est exactement nulle.
Un autre cas particulier est celui où l'angle de contact est exactement de 180°. L'eau avec du téflon spécialement préparé s'en approche. L'angle de contact de 180° se produit lorsque la tension superficielle liquide-solide est exactement égale à la tension superficielle liquide-air.
γ l a = γ l s - γ s a > 0 θ = 180 ∘ {\displaystyle \gamma _{\mathrm {la} =\ \ \ gamma _{\mathrm {ls} }-\gamma _{\mathrm {sa} }\ >\ 0\qquad \theta \ =\ 180^{\circ}}
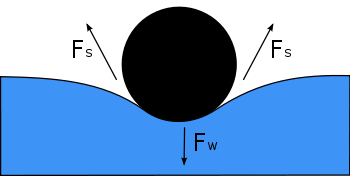
Le diagramme montre, en coupe transversale, une aiguille flottant à la surface de l'eau. Son poids, Fw, abaisse la surface, et est équilibré par les forces de tension superficielle de chaque côté, Fs, qui sont chacune parallèles à la surface de l'eau aux points où elle entre en contact avec l'aiguille. Remarquez que les composantes horizontales des deux flèches Fs pointent dans des directions opposées, donc elles s'annulent, mais les composantes verticales pointent dans la même direction et s'additionnent donc pour équilibrer Fw.
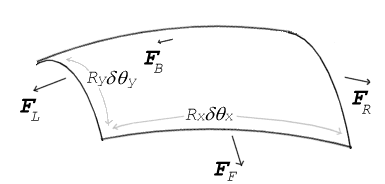
Forces de tension superficielle agissant sur une minuscule surface (différentielle). δθx et δθy indiquent l'importance de la flexion sur les dimensions de la parcelle. L'équilibre entre les forces de tension et la pression conduit à l'équation de Young-Laplace

Surface minimale
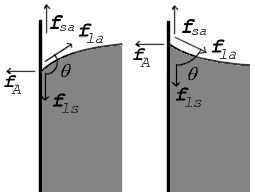
Forces au point de contact indiquées pour un angle de contact supérieur à 90° (gauche) et inférieur à 90° (droite)
Méthodes de mesure
Comme la tension superficielle se manifeste par divers effets, elle offre plusieurs voies pour sa mesure. La méthode optimale dépend de la nature du liquide à mesurer, des conditions dans lesquelles sa tension doit être mesurée et de la stabilité de sa surface lorsqu'elle est déformée.
- La méthode Du Noüy Ring : La méthode traditionnelle utilisée pour mesurer la tension superficielle ou interfaciale. Les propriétés de mouillage de la surface ou de l'interface n'ont que peu d'influence sur cette technique de mesure. On mesure la traction maximale exercée sur l'anneau par la surface.
- La méthode Du Noüy-Padday : Une version minimisée de la méthode Du Noüy utilise une aiguille métallique de petit diamètre au lieu d'un anneau, en combinaison avec une microbalance à haute sensibilité pour enregistrer l'effort maximal. L'avantage de cette méthode est que de très petits volumes d'échantillons (jusqu'à quelques dizaines de microlitres) peuvent être mesurés avec une très grande précision, sans qu'il soit nécessaire de corriger la flottabilité (pour une aiguille ou plutôt une tige, avec une géométrie appropriée). De plus, la mesure peut être effectuée très rapidement, au minimum en 20 secondes environ. Les premiers tensiomètres multicanaux commerciaux [CMCeeker] ont été récemment construits sur ce principe.
- Méthode de la plaque Wilhelmy : Méthode universelle particulièrement adaptée au contrôle de la tension superficielle sur de longs intervalles de temps. Une plaque verticale de périmètre connu est fixée à une balance, et la force due au mouillage est mesurée.
- Méthode de la goutte tournante : Cette technique est idéale pour mesurer les faibles tensions interfaciales. Le diamètre d'une goutte dans une phase lourde est mesuré alors que les deux sont en rotation.
- Méthode de chute du pendentif : Cette technique permet de mesurer la tension superficielle et interfaciale, même à des températures et des pressions élevées. La géométrie d'une goutte est analysée optiquement. Pour plus de détails, voir Goutte.
- Méthode de la pression de bulle (méthode de Jaeger) : Technique de mesure permettant de déterminer la tension superficielle à court terme. La pression maximale de chaque bulle est mesurée.
- Méthode du volume de chute : Méthode permettant de déterminer la tension interfaciale en fonction de l'âge de l'interface. Un liquide d'une densité est pompé dans un second liquide d'une densité différente et le temps entre les gouttes produites est mesuré.
- Méthode de l'élévation capillaire : L'extrémité d'un capillaire est immergée dans la solution. La hauteur à laquelle la solution atteint l'intérieur du capillaire est liée à la tension de surface par l'équation discutée ci-dessous.
- Méthode stalagmétrique : Méthode de pondération et de lecture d'une goutte de liquide.
- Méthode de largage de sessile : Méthode permettant de déterminer la tension et la densité de surface en plaçant une goutte sur un substrat et en mesurant l'angle de contact (voir technique de la goutte sessile).
- Fréquence vibratoire des gouttes en lévitation : La tension superficielle du superfluide 4He a été mesurée en étudiant la fréquence naturelle des oscillations vibratoires des gouttes maintenues dans l'air par des moyens magnétiques. Cette valeur est estimée à 0,375 dyn/cm à T = 0° K.

La tension de surface peut être mesurée par la méthode de la goutte pendante sur un goniomètre.
Effets
Liquide dans un tube vertical
Un baromètre à mercure de style ancien se compose d'un tube de verre vertical d'environ 1 cm de diamètre partiellement rempli de mercure, et d'un vide (appelé vide de Torricelli) dans le volume non rempli (voir schéma à droite). Remarquez que le niveau de mercure au centre du tube est plus élevé qu'aux bords, ce qui donne à la surface supérieure du mercure une forme de dôme. Le centre de masse de toute la colonne de mercure serait légèrement plus bas si la surface supérieure du mercure était plane sur toute la section du tube. Mais la surface supérieure en forme de dôme donne une surface légèrement inférieure à la masse totale du mercure. Là encore, les deux effets se combinent pour minimiser l'énergie potentielle totale. Une telle forme de surface est connue sous le nom de ménisque convexe.
Nous considérons la surface de toute la masse de mercure, y compris la partie de la surface qui est en contact avec le verre, car le mercure n'adhère pas du tout au verre. La tension superficielle du mercure agit donc sur toute sa surface, y compris là où il est en contact avec le verre. Si, au lieu du verre, le tube était en cuivre, la situation serait très différente. Le mercure adhère de manière agressive au cuivre. Ainsi, dans un tube en cuivre, le niveau de mercure au centre du tube sera plus faible qu'aux bords (c'est-à-dire qu'il s'agirait d'un ménisque concave). Dans une situation où le liquide adhère aux parois de son récipient, nous considérons que la partie de la surface du liquide qui est en contact avec le récipient a une tension superficielle négative. Le fluide travaille alors pour maximiser la surface de contact. Donc, dans ce cas, augmenter la surface de contact avec le récipient diminue plutôt qu'augmente l'énergie potentielle. Cette diminution est suffisante pour compenser l'augmentation de l'énergie potentielle associée au soulèvement du fluide près des parois du conteneur.
Si un tube est suffisamment étroit et que l'adhérence du liquide à ses parois est suffisamment forte, la tension superficielle peut aspirer le liquide vers le haut du tube par un phénomène appelé capillarité. La hauteur à laquelle la colonne est soulevée est donnée par :
h = 2 γ l a cos θ ρ g r {\displaystyle h\ =\ {\frac {2\gamma _{\mathrm {la} }\cos \theta }{\rho gr}}}
où
· h {\displaystyle \scriptstyle h}
· γ l a {\displaystyle \scriptstyle \gamma _{\mathrm {la} }}
· ρ {\displaystyle \scriptstyle \rho }
· r {\displaystyle \scriptstyle r}
· g {\displaystyle \scriptstyle g}
· θ {\displaystyle \scriptstyle \theta }

Des flaques d'eau sur une surface
En versant du mercure sur une feuille de verre plane et horizontale, on obtient une flaque d'une épaisseur perceptible. La flaque ne s'étendra que jusqu'à ce qu'elle ait un peu moins d'un demi-centimètre d'épaisseur, et pas moins. Là encore, cela est dû à l'action de la forte tension superficielle du mercure. La masse liquide s'aplatit car cela amène la plus grande partie du mercure à un niveau aussi bas que possible, mais la tension superficielle, en même temps, agit pour réduire la surface totale. Le résultat est le compromis d'une flaque d'une épaisseur presque fixe.
La même démonstration de la tension superficielle peut être faite avec de l'eau, de l'eau de chaux ou même du sel, mais seulement si le liquide n'adhère pas au matériau de la surface plane. La cire est une telle substance. L'eau versée sur une surface de cire lisse, plane et horizontale, par exemple une feuille de verre cirée, se comportera de la même manière que le mercure versé sur le verre.
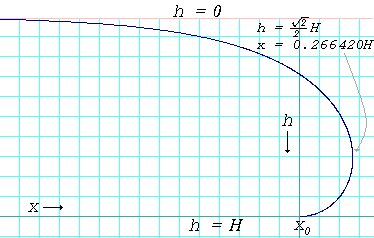
L'épaisseur d'une flaque de liquide sur une surface dont l'angle de contact est de 180° est donnée par
h = 2 γ g ρ {\displaystyle h\ =\ 2{\sqrt {\frac {\gamma }{g\rho}}}
où
| h {\displaystyle \scriptstyle h} |
| γ {\displaystyle \scriptstyle \gamma } |
| g {\displaystyle \scriptstyle g} |
| ρ {\displaystyle \scriptstyle \rho } |
En réalité, l'épaisseur des flaques sera légèrement inférieure à ce qui est prévu par la formule ci-dessus car très peu de surfaces ont un angle de contact de 180° avec un quelconque liquide. Lorsque l'angle de contact est inférieur à 180°, l'épaisseur est donnée par :
h = 2 γ l a ( 1 - cos θ ) g ρ . displaystyle h\ =\ {\sqrt {\frac {2\gamma _{\mathrm {la} }\left(1-\cos \theta \right)}{g\rho }}}. }
Pour le mercure sur verre, γHg = 487 dyn/cm, ρHg = 13,5 g/cm3 et θ = 140°, ce qui donne hHg = 0,36 cm. Pour l'eau sur la paraffine à 25 °C, γ = 72 dyn/cm, ρ = 1,0 g/cm3, et θ = 107°, ce qui donne hH2O = 0,44 cm.
La formule prévoit également que lorsque l'angle de contact est de 0°, le liquide se répand en une couche micro-fine sur la surface. Une telle surface est dite entièrement mouillable par le liquide.
La décomposition des cours d'eau en gouttes
Dans la vie quotidienne, nous observons tous qu'un jet d'eau sortant d'un robinet se brise en gouttelettes, quelle que soit la fluidité du jet émis par le robinet. Cela est dû à un phénomène appelé instabilité du Plateau-Rayleigh, qui est entièrement une conséquence des effets de la tension superficielle.
L'explication de cette instabilité commence par l'existence de minuscules perturbations dans le cours d'eau. Ces perturbations sont toujours présentes, même si le courant est très régulier. Si les perturbations sont résolues en composantes sinusoïdales, nous constatons que certaines composantes croissent avec le temps tandis que d'autres se dégradent avec le temps. Parmi celles qui croissent avec le temps, certaines croissent à un rythme plus rapide que d'autres. Le fait qu'un composant se désintègre ou croisse, et la vitesse à laquelle il croît, est entièrement fonction de son nombre d'ondes (une mesure du nombre de pics et de creux par centimètre) et des rayons du courant cylindrique d'origine.
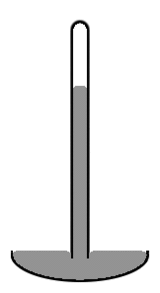
Schéma d'un baromètre à mercure
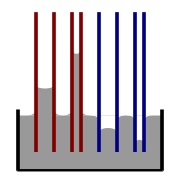
Illustration de la montée et de la descente capillaires. Rouge=angle de contact inférieur à 90° ; bleu=angle de contact supérieur à 90
Courbe de profil du bord d'une flaque d'eau où l'angle de contact est de 180°. La courbe est donnée par la formule : x - x 0 = 1 2 H cosh - 1 ( H h ) - H 1 - h 2 H 2 {\displaystyle \scriptstyle x-x_{0}\ =\ {\frac {1}{2}}H\cosh ^{-1}\left({\frac {H}{h}}\right)-H{\sqrt {1-{\frac {h^{2}}{H^{2}}}}}}

De petites flaques d'eau sur une surface lisse et propre ont une épaisseur perceptible.
Illustration de la manière dont un angle de contact plus faible entraîne une réduction de la profondeur de la flaque
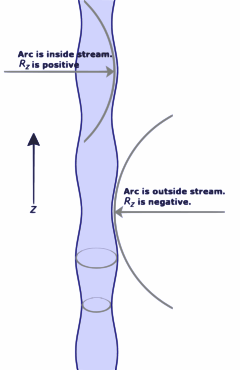
Etape intermédiaire d'un jet qui se brise en gouttes. Les rayons de courbure dans la direction axiale sont indiqués. L'équation pour le rayon du jet est R ( z ) = R 0 + A k cos ( k z ) {\displaystyle \scriptstyle R\left(z\right)=R_{0}+A_{k}\cos \left(kz\right)}


Tableau de données
| Tension superficielle de divers liquides en dyn/cm par rapport à l'airLes | ||
| Liquid | Température °C | Tension de surface, γ |
| Acide acétique | 20 | 27.6 |
| Acide acétique (40,1%) + Eau | 30 | 40.68 |
| Acide acétique (10,0%) + Eau | 30 | 54.56 |
| Acétone | 20 | 23.7 |
| Éther diéthylique | 20 | 17.0 |
| Éthanol | 20 | 22.27 |
| Éthanol (40%) + eau | 25 | 29.63 |
| Éthanol (11,1 %) + eau | 25 | 46.03 |
| Glycérol | 20 | 63 |
| n-Hexane | 20 | 18.4 |
| Acide chlorhydrique 17,7M en solution aqueuse | 20 | 65.95 |
| Isopropanol | 20 | 21.7 |
| Azote liquide | -196 | 8.85 |
| Mercure | 15 | 487 |
| Méthanol | 20 | 22.6 |
| n-Octane | 20 | 21.8 |
| Chlorure de sodium 6,0 M en solution aqueuse | 20 | 82.55 |
| Saccharose (55%) + eau | 20 | 76.45 |
| Eau | 0 | 75.64 |
| Eau | 25 | 71.97 |
| Eau | 50 | 67.91 |
| Eau | 100 | 58.85 |
Galerie d'effets
· 
Rupture d'une feuille d'eau en mouvement rebondissant sur une cuillère.
· 
Photo de l'eau qui coule et qui adhère à une main. La tension de surface crée la nappe d'eau entre le flux et la main.
· 
Une bulle de savon équilibre les forces de tension superficielle contre la pression pneumatique interne.
· 
La tension de surface empêche une pièce de s'enfoncer : la pièce est incontestablement plus dense que l'eau, elle doit donc déplacer un volume supérieur au sien pour que la flottabilité équilibre la masse.
· 
Une marguerite. La totalité de la fleur se trouve sous le niveau de la surface libre (non perturbée). L'eau monte doucement sur son bord. La tension superficielle empêche l'eau de remplir l'air entre les pétales et éventuellement de submerger la fleur.
· 
Un trombone en métal flotte sur l'eau. On peut généralement en ajouter plusieurs avec précaution sans que l'eau ne déborde.
· .jpg)
Une pièce de monnaie en aluminium flotte à la surface de l'eau à 10 °C. Tout poids supplémentaire ferait tomber la pièce au fond.
Questions et réponses
Q : Qu'est-ce que la tension superficielle ?
R : La tension superficielle est un effet où la surface d'un liquide est forte, et peut retenir un poids. Elle fait que certaines petites choses peuvent flotter à la surface alors qu'elles ne le pourraient pas normalement, et permet à certains insectes (par exemple, les stridents d'eau) de courir à la surface de l'eau.
Q : Qu'est-ce qui provoque la tension superficielle ?
R : La tension superficielle est due au fait que les molécules du liquide sont attirées les unes vers les autres (cohésion).
Q : Quelles sont les dimensions de la tension superficielle ?
R : La tension superficielle a la dimension de la force par unité de longueur, ou de l'énergie par unité de surface. Les deux sont équivalents, mais lorsqu'on se réfère à l'énergie par unité de surface, les gens utilisent le terme d'énergie de surface - qui est un terme plus général dans le sens où il s'applique également aux solides et pas seulement aux liquides.
Q : Comment la tension superficielle affecte-t-elle la science des matériaux ?
R : En science des matériaux, la tension de surface est utilisée pour désigner soit la contrainte de surface, soit l'énergie libre de surface.
Q : Comment la cohésion contribue-t-elle à la tension de surface ?
R : La cohésion contribue à la tension superficielle en attirant les molécules d'un liquide les unes vers les autres, ce qui crée un lien fort à sa surface, capable de supporter le poids et de permettre à certains objets ou créatures (par exemple, les stridents) d'interagir avec lui différemment de ce qu'ils pourraient faire autrement.
Q : En quoi cette propriété diffère-t-elle des autres propriétés des liquides ?
R : Cette propriété diffère des autres propriétés des liquides car elle affecte la façon dont les objets interagissent avec eux sur leurs surfaces plutôt qu'à l'intérieur de celles-ci ou par leur comportement global.
Rechercher dans l'encyclopédie