Intégrale de surface
En mathématiques, une intégrale de surface est une intégrale définie prise sur une surface (qui peut être une courbe établie dans l'espace). Tout comme une intégrale linéaire gère une dimension ou une variable, une intégrale de surface peut être considérée comme une double intégrale dans deux dimensions. Étant donné une surface, on peut intégrer sur ses champs scalaires (c'est-à-dire des fonctions qui renvoient des nombres comme valeurs), et des champs vectoriels (c'est-à-dire des fonctions qui renvoient des vecteurs comme valeurs).
Les intégrales de surface ont des applications en physique, notamment avec la théorie classique de l'électromagnétisme.

La définition de l'intégrale de surface repose sur la division de la surface en petits éléments de surface.

Une illustration d'un élément de surface unique. Ces éléments sont rendus infiniment petits, par le processus de limitation, de manière à se rapprocher de la surface.
Intégrales de surface des champs scalaires
Considérons une surface S sur laquelle un champ scalaire f est défini. Si l'on considère que S est constituée d'un matériau quelconque, et que pour chaque x dans S le nombre f(x) est la densité du matériau à x, alors l'intégrale de surface de f sur S est la masse par unité d'épaisseur de S. (Ceci n'est vrai que si la surface est une coquille infiniment mince.) Une approche du calcul de l'intégrale de surface consiste à diviser la surface en plusieurs très petits morceaux, à supposer que sur chaque morceau la densité est approximativement constante, à trouver la masse par unité d'épaisseur de chaque morceau en multipliant la densité du morceau par sa surface, puis à additionner les nombres résultants pour trouver la masse totale par unité d'épaisseur de S.
Pour trouver une formule explicite pour l'intégrale de surface, les mathématiciens paramètrent S en considérant sur S un système de coordonnées curvilignes, comme la latitude et la longitude sur une sphère. Soit une telle paramétrisation x(s, t), où (s, t) varie dans une certaine région T du plan. Ensuite, l'intégrale de surface est donnée par
∫ S f d S = ∬ T f ( x ( s , t ) ) | ∂ x ∂ s × ∂ x ∂ t | d s d t {\displaystyle \int _{S}f\,dS=\iint _{T}f(\mathbf {x} (s,t))\left|{\partial \mathbf {x} \over \partial s}\times {\partial \mathbf {x} \over \partial t}\right|ds\,dt}
où l'expression entre les barres à droite est la grandeur du produit croisé des dérivées partielles de x(s, t).
Par exemple, pour trouver la surface d'une forme fonctionnelle générale, disons z = f ( x , y )
A = ∫ S d S = ∬ T ‖ ∂ r ∂ x × ∂ r ∂ y ‖ d x d y {\displaystyle A=\int _{S}\,dS=\iint _{T}\left\|{\partial \mathbf {r} \over \partial x}\times {\partial \mathbf {r} \over \partial y}\right\|dx\,dy}
où r = ( x , y , z ) = ( x , y , f ( x , y ) {\displaystyle \mathbf {r} =(x,y,z)=(x,y,f(x,y))}


A = ∬ T ‖ ( 1 , 0 , ∂ f ∂ x ) × ( 0 , 1 , ∂ f ∂ y ) ‖ d x d y = ∬ T ‖ ( - ∂ f ∂ x , - ∂ f ∂ y , 1 ) ‖ d x d y = ∬ T ( ∂ f ∂ x ) 2 + ( ∂ f ∂ y ) 2 + 1 d x d y {\displaystyle {\begin{aligned}A&.{}=\iint _{T}\left\|\left(1,0,{\partial f \over \partial x}\right)\times \left(0,1,{\partial f \over \partial y}\right)\|dx\,dy\&{}=\iint _{T}\left\|\left(-{\partial f \over \partial x},-{\partial f \over \partial y},1\right)\|dx\,dy\&{}=\iint _{T}{\sqrt {\left({\partial f \over \partial x}\right)^{2}+\left({\partial f \over \partial y}\right)^{2}+1}}\,\,dx\,dy\end{aligned}}}
qui est la formule utilisée pour la surface d'une forme fonctionnelle générale. On peut reconnaître le vecteur de la deuxième ligne ci-dessus comme étant le vecteur normal à la surface.
Notez qu'en raison de la présence du produit croisé, les formules ci-dessus ne fonctionnent que pour les surfaces encastrées dans l'espace tridimensionnel.
Intégrales de surface des champs vectoriels
Considérons un champ vectoriel v sur S, c'est-à-dire que pour chaque x dans S, v(x) est un vecteur.
L'intégrale de surface peut être définie par composante selon la définition de l'intégrale de surface d'un champ scalaire ; le résultat est un vecteur. Par exemple, cela s'applique au champ électrique en un point fixe dû à une surface chargée électriquement, ou à la gravité en un point fixe dû à une feuille de matériau. Il peut également calculer le flux magnétique à travers une surface.
Alternativement, les mathématiciens peuvent intégrer la composante normale du champ vectoriel ; le résultat est un scalaire. Un exemple est un fluide s'écoulant à travers S, tel que v(x) détermine la vitesse du fluide à x. Le flux est défini comme la quantité de fluide s'écoulant à travers S dans une unité de temps.
Cette illustration implique que si le champ vectoriel est tangent à S en chaque point, alors le flux est nul, car le fluide s'écoule juste parallèlement à S, et n'entre ni ne sort. Cela implique également que si v ne s'écoule pas seulement le long de S, c'est-à-dire si v a à la fois une composante tangentielle et une composante normale, alors seule la composante normale contribue au flux. Sur la base de ce raisonnement, pour trouver le flux, nous devons prendre le produit ponctuel de v avec la surface unitaire normale à S en chaque point, ce qui nous donnera un champ scalaire, et intégrer le champ obtenu comme ci-dessus. Cela donne la formule
∫ S v ⋅ d S = ∫ S ( v ⋅ n ) d S = ∬ T v ( x ( s , t ) ) ⋅ ( ∂ x ∂ s × ∂ x ∂ t ) d s d t . {\displaystyle \int _{S}{\mathbf {v} }\cdot \,d{\mathbf {S} }=\int _{S}({\mathbf {v} }\cdot {\mathbf {n} })\,dS=\iint _{T}{\mathbf {v} }(\mathbf {x} (s,t))\cdot \left({\partial \mathbf {x} \over \partial s}\times {\partial \mathbf {x} \over \partial t}\right)ds\,dt. }
Le produit croisé à droite de cette expression est une normale de surface déterminée par la paramétrisation.
Cette formule définit l'intégrale de gauche (notez le point et la notation du vecteur pour l'élément de surface).
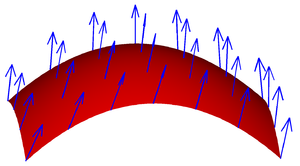
Un champ vectoriel sur une surface.
Théorèmes impliquant des intégrales de surface
Divers résultats utiles pour les intégrales de surface peuvent être obtenus en utilisant la géométrie différentielle et le calcul vectoriel, comme le théorème de divergence, et sa généralisation, le théorème de Stokes.
Questions avancées
Modification du paramétrage
La discussion ci-dessus a défini l'intégrale de surface en utilisant une paramétrisation de la surface S. Une surface donnée peut avoir plusieurs paramétrisations. Par exemple, lorsque les positions du pôle Nord et du pôle Sud sont déplacées sur une sphère, la latitude et la longitude changent pour tous les points de la sphère. Il est alors naturel de se demander si la définition de l'intégrale de la surface dépend de la paramétrisation choisie. Pour les intégrales des champs scalaires, la réponse à cette question est simple, la valeur de l'intégrale de surface sera la même quelle que soit la paramétrisation utilisée.
Les intégrales des champs vectoriels sont plus compliquées, car la normale à la surface est impliquée. Les mathématiciens ont prouvé que, compte tenu de deux paramétrisations de la même surface, dont les normales de surface pointent dans la même direction, les deux paramétrisations donnent la même valeur pour l'intégrale de surface. Si, cependant, les normales de ces paramétrisations pointent dans des directions opposées, la valeur de l'intégrale de surface obtenue par une paramétrisation est la négative de celle obtenue par l'autre paramétrisation. Il s'ensuit qu'étant donné une surface, nous n'avons pas besoin de nous en tenir à une paramétrisation unique ; mais, lors de l'intégration de champs vectoriels, nous devons décider à l'avance de la direction vers laquelle la normale pointera et choisir ensuite toute paramétrisation compatible avec cette direction.
Travail de paramétrage sur certaines parties de la surface
Un autre problème est que parfois les surfaces n'ont pas de paramétrisations qui couvrent toute la surface ; c'est le cas par exemple pour la surface d'un cylindre (de hauteur finie). La solution évidente est alors de diviser cette surface en plusieurs morceaux, de calculer l'intégrale de la surface sur chaque morceau, puis de les additionner tous. C'est effectivement ainsi que les choses fonctionnent, mais lorsqu'on intègre des champs vectoriels, il faut encore une fois faire attention à la façon de choisir le vecteur de pointage normal pour chaque morceau de la surface, de sorte que lorsque les morceaux sont recomposés, les résultats soient cohérents. Pour le cylindre, cela signifie que si nous décidons que pour la région latérale la normale pointera vers le corps, alors pour les parties circulaires supérieure et inférieure la normale doit pointer vers le corps également.
Normales de surface incohérentes
Enfin, il y a des surfaces qui n'ont pas de normale en chaque point avec des résultats cohérents (par exemple, la bande de Möbius). Si une telle surface est divisée en morceaux, sur chaque morceau on choisit une paramétrisation et une normale de surface correspondante, et que les morceaux sont remis ensemble, les vecteurs normaux provenant des différents morceaux ne peuvent pas être réconciliés. Cela signifie qu'à une certaine jonction entre deux pièces, les vecteurs normaux seront dirigés dans des directions opposées. Une telle surface est dite non orientable. Les champs vectoriels ne peuvent pas être intégrés sur des surfaces non orientables.
Pages connexes
- Théorème de la divergence
- Le théorème de Stokes
- Intégrale de la ligne
- Intégralité du volume
- Système de coordonnées cartésiennes
- Éléments de volume et de surface dans un système de coordonnées sphériques
- Éléments de volume et de surface dans un système de coordonnées cylindriques
- La méthode Holstein-Herring
Rechercher dans l'encyclopédie



