Écart type
L'écart-type est un nombre utilisé pour indiquer comment les mesures d'un groupe sont réparties par rapport à la moyenne ou à la valeur attendue. Un faible écart-type signifie que la plupart des chiffres sont proches de la moyenne. Un écart-type élevé signifie que les chiffres sont plus étalés.
La marge d'erreur signalée est généralement égale à deux fois l'écart type. Les scientifiques signalent généralement l'écart type des nombres par rapport au nombre moyen dans les expériences. Ils décident souvent que seules les différences supérieures à deux ou trois fois l'écart-type sont importantes. L'écart-type est également utile dans le domaine de l'argent, où l'écart-type des intérêts gagnés montre à quel point les intérêts gagnés par une personne peuvent être différents de la moyenne.
Souvent, seul un échantillon ou une partie d'un groupe peut être mesuré. On peut alors trouver un nombre proche de l'écart-type pour l'ensemble du groupe grâce à une équation légèrement différente appelée écart-type de l'échantillon, expliquée ci-dessous.
.png)
Un tracé d'une distribution normale (ou courbe en cloche). Chaque bande colorée a une largeur d'un écart-type.
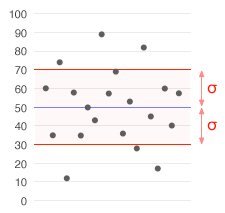
Un ensemble de données avec une moyenne de 50 (indiqué en bleu) et un écart-type (σ) de 20.
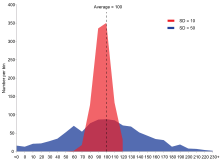
Exemple de deux échantillons de population ayant la même moyenne et des écarts-types différents. La population rouge a une moyenne de 100 et un écart-type de 10 ; la population bleue a une moyenne de 100 et un écart-type de 50.
Exemple de base
Considérez un groupe ayant les huit numéros suivants :
2 , 4 , 4 , 4 , 5 , 5 , 7 , 9 {\displaystyle 2,\ 4,\ 4,\ 4,\ 5,\ 5,\ 7,\ 9}
Ces huit chiffres ont une moyenne de 5 :
2 + 4 + 4 + 4 + 5 + 5 + 7 + 9 8 = 5 {\frac {2+4+4+4+5+5+7+9}{8}}=5}
Pour calculer l'écart-type de la population, il faut d'abord trouver la différence entre chaque nombre de la liste et la moyenne. Ensuite, mettez au carré le résultat de chaque différence :
( 2 - 5 ) 2 = ( - 3 ) 2 = 9 ( 5 - 5 ) 2 = 0 2 = 0 ( 4 - 5 ) 2 = ( - 1 ) 2 = 1 ( 5 - 5 ) 2 = 0 2 = 0 ( 4 - 5 ) 2 = ( - 1 ) 2 = 1 ( 7 - 5 ) 2 = 2 2 = 4 ( 4 - 5 ) 2 = ( - 1 ) 2 = 1 ( 9 - 5 ) 2 = 4 2 = 16 {\displaystyle {\begin{array}{lll}(2-5)^{2}=(-3)^{2}=9&&(5-5)^{2}=0^{2}=0\\(4-5)^{2}=(-1)^{2}=1&&(5-5)^{2}=0^{2}=0\\(4-5)^{2}=(-1)^{2}=1&&(7-5)^{2}=2^{2}=4\\(4-5)^{2}=(-1)^{2}=1&&(9-5)^{2}=4^{2}=16\\\end{array}}}
Ensuite, trouvez la moyenne de ces valeurs (somme divisée par le nombre de chiffres). Enfin, prenez la racine carrée :
( 9 + 1 + 1 + 1 + 0 + 0 + 4 + 16 ) 8 = 2 {\displaystyle {\sqrt {\frac {(9+1+1+1+1+0+0+4+16)}{8}}}=2}
La réponse est l'écart-type de la population. La formule n'est vraie que si les huit chiffres avec lesquels nous avons commencé sont le groupe entier. S'ils ne sont qu'une partie du groupe choisie au hasard, alors nous devrions utiliser 7 (qui est n - 1) au lieu de 8 (qui est n) dans le bas (dénominateur) de l'avant-dernière étape. La réponse est alors l'écart-type de l'échantillon. C'est ce que l'on appelle la correction de Bessel.
Plus d'exemples
Un exemple concret, un peu plus difficile : La taille moyenne des hommes adultes aux États-Unis est de 70", avec un écart type de 3". Un écart-type de 3" signifie que la plupart des hommes (environ 68%, en supposant une distribution normale) ont une taille de 3" de plus à 3" de moins que la moyenne (67-73") - un écart-type. Presque tous les hommes (environ 95%) ont une taille de 6" plus grande à 6" plus petite que la moyenne (64"-76") - deux écarts types. Trois écarts types incluent tous les chiffres pour 99,7 % de la population étudiée. Cela est vrai si la distribution est normale (en forme de cloche).
Si l'écart-type était de zéro, tous les hommes mesureraient alors exactement 70 pouces. Si l'écart-type était de 20", certains hommes seraient beaucoup plus grands ou beaucoup plus petits que la moyenne, avec une fourchette typique d'environ 50"-90".
Dans un autre exemple, chacun des trois groupes {0, 0, 14, 14}, {0, 6, 8, 14} et {6, 6, 8, 8} a une moyenne de 7. Mais leurs écarts-types sont de 7, 5 et 1. Le troisième groupe a un écart type beaucoup plus faible que les deux autres car ses nombres sont tous proches de 7. L'idée de base est que l'écart-type nous indique à quelle distance de la moyenne les autres nombres ont tendance à se trouver. Il aura les mêmes unités que les nombres eux-mêmes. Si, par exemple, le groupe {0, 6, 8, 14} correspond à l'âge d'un groupe de quatre frères en années, la moyenne est de 7 ans et l'écart-type de 5 ans.
L'écart-type peut servir de mesure de l'incertitude. En science, par exemple, l'écart-type d'un groupe de mesures répétées aide les scientifiques à savoir dans quelle mesure ils sont sûrs du nombre moyen. Lorsque l'on décide si les mesures d'une expérience concordent avec une prédiction, l'écart-type de ces mesures est très important. Si le nombre moyen des expériences est trop éloigné du nombre prédit (la distance étant mesurée en écarts-types), alors la théorie testée peut ne pas être correcte. Voir intervalle de prédiction.
Exemples d'application
Pour comprendre l'écart-type d'un ensemble de valeurs, il faut savoir quelle est la différence attendue par rapport à la "moyenne".
Météo
À titre d'exemple simple, considérons les températures élevées moyennes quotidiennes de deux villes, l'une située à l'intérieur des terres et l'autre près de l'océan. Il est utile de comprendre que la fourchette des températures élevées quotidiennes des villes situées près de l'océan est plus petite que celle des villes situées à l'intérieur des terres. Ces deux villes peuvent avoir la même moyenne de températures maximales quotidiennes. Toutefois, l'écart type de la température maximale quotidienne pour la ville côtière sera inférieur à celui de la ville située à l'intérieur des terres.
Sports
Une autre façon de voir les choses est de considérer les équipes sportives. Dans tout sport, il y aura des équipes qui sont bonnes dans certains domaines et pas dans d'autres. Les équipes qui sont les mieux classées ne présenteront pas beaucoup de différences de capacités. Elles réussissent dans la plupart des catégories. Plus l'écart-type de leurs capacités est faible dans chaque catégorie, plus elles sont équilibrées et cohérentes. En revanche, les équipes dont l'écart type est plus élevé seront moins prévisibles. Une équipe qui est généralement mauvaise dans la plupart des catégories aura un faible écart-type. Une équipe qui est généralement bonne dans la plupart des catégories aura également un faible écart type. Cependant, une équipe avec un écart-type élevé peut être le type d'équipe qui marque beaucoup de points (forte attaque) mais qui laisse également l'autre équipe marquer beaucoup de points (faible défense).
Pour savoir à l'avance quelles équipes vont gagner, on peut notamment examiner les écarts types des différentes "statistiques" des équipes. Des chiffres différents de ceux attendus peuvent faire correspondre les forces et les faiblesses pour montrer quelles raisons peuvent être les plus importantes pour savoir quelle équipe va gagner.
En course, on mesure le temps qu'un pilote met pour terminer chaque tour de piste. Un pilote ayant un faible écart-type des temps au tour est plus régulier qu'un pilote ayant un écart-type plus élevé. Ces informations peuvent être utilisées pour aider à comprendre comment un pilote peut réduire le temps nécessaire pour terminer un tour.
Argent
En argent, l'écart-type peut signifier le risque qu'un prix monte ou descende (actions, obligations, biens immobiliers, etc.). Il peut également signifier le risque qu'un groupe de prix augmente ou diminue (fonds communs de placement gérés activement, fonds communs de placement indiciels ou ETF). Le risque est l'une des raisons qui motivent les décisions d'achat. Le risque est un nombre que les gens peuvent utiliser pour savoir combien d'argent ils peuvent gagner ou perdre. Lorsque le risque augmente, le rendement d'un investissement peut être plus élevé que prévu (l'écart type "plus"). Cependant, un investissement peut aussi perdre plus d'argent que prévu (l'écart type "moins").
Par exemple, une personne devait choisir entre deux actions. Au cours des 20 dernières années, l'action A a eu un rendement moyen de 10 %, avec un écart type de 20 points de pourcentage (pp). L'action B, au cours des 20 dernières années, a eu un rendement moyen de 12 %, mais avec un écart-type plus élevé de 30 points de pourcentage (pp). En réfléchissant au risque, la personne peut décider que l'action A est le choix le plus sûr. Même si elle ne gagne pas autant d'argent, elle n'en perdra probablement pas beaucoup non plus. La personne peut penser que la moyenne de l'action B, plus élevée de 2 points, ne vaut pas les 10 pp d'écart type supplémentaires (risque plus élevé ou incertitude du rendement attendu).
Règles pour les numéros normalement distribués
La plupart des équations mathématiques de l'écart-type supposent que les nombres sont normalement distribués. Cela signifie que les nombres sont répartis d'une certaine manière des deux côtés de la valeur moyenne. La distribution normale est également appelée distribution gaussienne car elle a été découverte par Carl Friedrich Gauss. Elle est souvent appelée courbe en cloche parce que les nombres s'étalent pour prendre la forme d'une cloche sur un graphique.
Les nombres ne sont normalement pas distribués s'ils sont regroupés d'un côté ou de l'autre de la valeur moyenne. Les nombres peuvent être étalés tout en étant normalement distribués. L'écart-type indique l'étendue de la répartition des nombres.

Le bleu foncé correspond à moins d'un écart type par rapport à la moyenne. Pour la distribution normale, cela comprend 68,27 % des chiffres ; tandis que deux écarts types par rapport à la moyenne (bleu moyen et foncé) comprennent 95,45 % ; trois écarts types (bleu clair, moyen et foncé) comprennent 99,73 % ; et quatre écarts types représentent 99,994 %.
Relation entre la moyenne et l'écart type
La moyenne et l'écart-type d'un ensemble de données sont généralement écrits ensemble. Une personne peut alors comprendre quel est le nombre moyen et dans quelle mesure les autres nombres du groupe sont répartis.
La façon dont un groupe de chiffres est réparti peut également être donnée par le coefficient de variation, qui est l'écart type divisé par la moyenne. Il s'agit d'un nombre sans dimension. Le coefficient de variation est souvent multiplié par 100 % et s'écrit en pourcentage.
Histoire
Le terme d'écart-type a été utilisé pour la première fois par écrit par Karl Pearson en 1894, après qu'il l'ait utilisé dans ses conférences. Il a remplacé les noms précédents pour la même idée : par exemple, Gauss a utilisé l'erreur moyenne.
Pages connexes
- Exactitude et précision
- Taille de l'échantillon
Questions et réponses
Q : Qu'est-ce que l'écart-type ?
R : L'écart-type est un nombre utilisé pour indiquer comment les mesures d'un groupe sont étalées par rapport à la moyenne (moyenne ou valeur attendue).
Q : Que signifie un faible écart-type ?
R : Un faible écart-type signifie que la plupart des chiffres sont proches de la moyenne.
Q : Que signifie un écart-type élevé ?
R : Un écart-type élevé signifie que les chiffres sont plus dispersés.
Q : Comment l'écart-type est-il utilisé dans le domaine monétaire ?
R : En argent, l'écart type sur les intérêts perçus montre à quel point les intérêts perçus par une personne peuvent être différents de la moyenne.
Q : Quand peut-on mesurer une partie seulement d'un groupe ?
R : Bien souvent, seul un échantillon, ou une partie d'un groupe, peut être mesuré.
Q : Comment l'écart-type de l'ensemble du groupe est-il représenté ?
R : L'écart type de tout le groupe est représenté par la lettre grecque َ {\displaystyle \sigma }. .
Q : Comment l'écart type de l'échantillon est-il représenté ?
R : L'écart-type de l'échantillon est représenté par s {\displaystyle s} .
Rechercher dans l'encyclopédie



