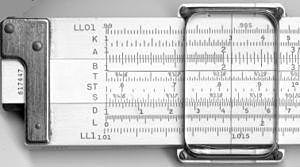
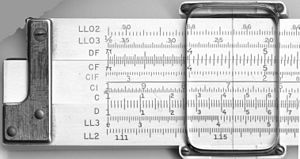
Règle à calcul

Concepts de base

Dans sa forme la plus élémentaire, la règle à calcul utilise deux échelles logarithmiques pour permettre une multiplication et une division rapides des nombres. Ces opérations courantes peuvent prendre beaucoup de temps et être source d'erreurs lorsqu'elles sont effectuées sur papier. Des règles plus complexes permettent d'effectuer d'autres calculs, tels que les racines carrées, les exponentielles, les logarithmes et les fonctions trigonométriques.

Les calculs mathématiques sont effectués en alignant une marque sur la bande centrale coulissante avec une marque sur l'une des bandes fixes. La position relative des autres marques peut alors être observée. Les nombres alignés avec les marques donnent la valeur approximative du produit, du quotient ou d'un autre résultat calculé.

L'utilisateur détermine l'emplacement du point décimal dans le résultat, en se basant sur une estimation mentale. La notation scientifique est utilisée pour suivre le point décimal dans des calculs plus formels. Les étapes d'addition et de soustraction dans un calcul sont généralement effectuées mentalement ou sur papier, et non sur la règle à calcul.

La plupart des règles à calcul comportent trois bandes linéaires de même longueur. Les bandes sont alignées en parallèle et s'emboîtent de manière à ce que la bande centrale puisse être déplacée dans le sens de la longueur par rapport aux deux autres. Les deux bandes extérieures sont fixées de manière à ce que leur position relative ne change pas.

Certaines règles à calcul (modèles "duplex") ont des écailles des deux côtés de la règle et de la bande de calcul, d'autres d'un côté des bandes extérieures et des deux côtés de la bande de calcul, d'autres encore d'un seul côté (règles "simplex"). Un curseur coulissant avec une ligne d'alignement verticale est utilisé pour trouver les points correspondants sur les échelles qui ne sont pas l'une à côté de l'autre ou, dans les modèles duplex, qui sont de l'autre côté de la règle. Le curseur peut également enregistrer un résultat intermédiaire sur n'importe laquelle des échelles.

Curseur sur une règle à calcul

Utilisation d'une règle à calcul

Multiplication

Un logarithme transforme les opérations de multiplication et de division en addition et en soustraction selon les règles log ( x y ) = log ( x ) + log ( y ) {\displaystyle \log(xy)=\log(x)+\log(y)} et log ( x / y ) = log ( x ) - log ( y ) {\displaystyle \log(x/y)=\log(x)-\log(y)} . Déplacement de l'échelle supérieure vers la droite d'une distance de log ( x ) en faisant correspondre le début de l'échelle du haut avec l'étiquette x {\style d'affichage x} en bas, aligne chaque nombre y {\style d'affichage y}. , à la position log ( y )/style d'affichage \log(y)} sur l'échelle supérieure, avec le nombre à la position log ( x ) + log ( y )/style d'affichage \log(x)+\log(y)} sur l'échelle inférieure. Parce que log ( x ) + log ( y ) = log ( x y ) {\displaystyle \log(x)+\log(y)=\log(xy)} Cette position sur l'échelle inférieure donne x y (style d'affichage xy) le produit de x et y. Par exemple, pour calculer 3*2, le 1 de l'échelle supérieure est déplacé vers le 2 de l'échelle inférieure. La réponse, 6, est lue sur l'échelle inférieure, où 3 se trouve sur l'échelle supérieure. En général, le 1 du haut de l'échelle est déplacé vers un facteur du bas de l'échelle et la réponse est lue au bas de l'échelle où l'autre facteur se trouve au haut de l'échelle.

Les opérations peuvent "sortir de l'échelle" ; par exemple, le diagramme ci-dessus montre que la règle à calcul n'a pas placé le 7 de l'échelle supérieure au-dessus d'un nombre de l'échelle inférieure, de sorte qu'elle ne donne aucune réponse pour 2×7. Dans ce cas, l'utilisateur peut faire glisser l'échelle supérieure vers la gauche jusqu'à ce que son index droit s'aligne sur le 2, en multipliant effectivement par 0,2 au lieu de 2, comme dans l'illustration ci-dessous :

Ici, l'utilisateur de la règle à calcul doit se souvenir d'ajuster le point décimal de manière appropriée pour corriger la réponse finale. Nous voulions trouver 2×7, mais nous avons plutôt calculé 0,2×7=1,4. La vraie réponse n'est donc pas 1,4 mais 14. La réinitialisation de la diapositive n'est pas la seule façon de traiter les multiplications qui entraîneraient des résultats hors échelle, comme 2×7 ; d'autres méthodes le font :

• (1) Utilisez les échelles à double décennie A et B.
• (2) Utilisez les échelles pliées. Dans cet exemple, mettez le 1 de C à gauche en face du 2 de D. Déplacez le curseur sur 7 sur CF, et lisez le résultat de DF.
• (3) Utilisez l'échelle inversée de l'IC. Positionnez le 7 sur l'échelle CI au-dessus du 2 sur l'échelle D, puis lisez le résultat sur l'échelle D, en dessous du 1 sur l'échelle CI. Puisque 1 se trouve à deux endroits sur l'échelle CI, l'un d'eux sera toujours sur l'échelle.
• (4) Utilisez à la fois l'échelle inversée de l'IC et l'échelle C. Alignez le 2 de CI avec le 1 de D, et lisez le résultat de D, sous le 7 de l'échelle C.

La méthode 1 est facile à comprendre, mais elle entraîne une perte de précision. La méthode 3 présente l'avantage de ne faire intervenir que deux échelles.

Division

L'illustration ci-dessous montre le calcul de 5,5/2. Le 2 sur l'échelle du haut est placé sur le 5,5 sur l'échelle du bas. Le 1 sur l'échelle supérieure se situe au-dessus du quotient, soit 2,75. Il existe plusieurs méthodes de division, mais la méthode présentée ici présente l'avantage que le résultat final ne peut pas être hors échelle, car on a le choix d'utiliser le 1 à chaque extrémité.

Autres opérations

En plus des échelles logarithmiques, certaines règles de calcul ont d'autres fonctions mathématiques codées sur d'autres échelles auxiliaires. Les plus populaires sont la trigonométrie, généralement sinus et tangente, le logarithme commun (log10) (pour prendre le log d'une valeur sur une échelle multiplicatrice), le logarithme naturel (ln) et les échelles exponentielles (^ex). Certaines règles comprennent une échelle de Pythagore, pour représenter les côtés des triangles, et une échelle pour représenter les cercles. D'autres comportent des échelles pour le calcul de fonctions hyperboliques. En ce qui concerne les règles linéaires, les échelles et leur étiquetage sont très normalisés, les variations ne se produisant généralement qu'en fonction des échelles incluses et de leur ordre :

A, B	des échelles logarithmiques à deux décennies, utilisées pour trouver les racines carrées et les carrés des nombres
C, D	échelles logarithmiques à une décennie
K	échelle logarithmique à trois décennies, utilisée pour trouver les racines cubiques et les cubes de nombres
CF, DF	des versions "pliées" des échelles C et D qui partent de π plutôt que de l'unité ; celles-ci sont pratiques dans deux cas. Premièrement, lorsque l'utilisateur estime qu'un produit sera proche de 10 mais n'est pas sûr qu'il sera légèrement inférieur ou légèrement supérieur à 10, les échelles pliées évitent la possibilité de sortir de l'échelle. Deuxièmement, en faisant le départ π plutôt que la racine carrée de 10, la multiplication ou la division par π (comme cela est courant dans les formules scientifiques et d'ingénierie) est simplifiée.
CI, DI, DIF	des échelles "inversées", allant de droite à gauche, utilisées pour simplifier les étapes de 1/x
S	utilisé pour trouver les sinus et les cosinus sur l'échelle D
T	utilisé pour trouver les tangentes et les cotangentes sur les échelles D et DI
ST, SRT	utilisé pour les sinus et les tangentes de petits angles et la conversion degré-radian
L	une échelle linéaire, utilisée avec les échelles C et D pour trouver des logarithmes en base 10 et des puissances de 10
LLn	un ensemble d'échelles logarithmiques, utilisées pour trouver des logarithmes et des exponentielles de nombres
Ln	une échelle linéaire, utilisée avec les échelles C et D pour trouver des logarithmes naturels (base e) et e x {\displaystyle e^{x}}

 

Les échelles à l'avant et à l'arrière d'une règle à calcul K&E 4081-3.

La règle à calcul binaire fabriquée par Gilson en 1931 exécutait une fonction d'addition et de soustraction limitée aux fractions.

Racines et pouvoirs

Il existe des échelles à une décennie (C et D), à deux décennies (A et B) et à trois décennies (K). Pour calculer x 2 {\displaystyle x^{2}} par exemple, localiser x sur l'échelle D et lire son carré sur l'échelle A. L'inversion de ce processus permet de trouver des racines carrées, et de même pour les puissances 3, 1/3, 2/3 et 3/2. Il faut faire attention lorsque la base, x, se trouve à plus d'un endroit sur son échelle. Par exemple, il y a deux neuf sur l'échelle A ; pour trouver la racine carrée de neuf, il faut utiliser le premier ; le second donne la racine carrée de 90.

Pour les problèmes de type xy, utilisez les échelles LL. Lorsque plusieurs échelles LL sont présentes, utilisez celle avec x. Tout d'abord, alignez le 1 le plus à gauche sur l'échelle C avec x sur l'échelle LL. Ensuite, trouvez y sur l'échelle C et descendez sur l'échelle LL avec x. Cette échelle indiquera la réponse. Si y est "hors de l'échelle", trouvez x y / 2 {\style d'affichage x^{y/2}} et équerrez-le en utilisant les échelles A et B comme décrit ci-dessus.

Trigonométrie

Les échelles S, T et ST sont utilisées pour les fonctions trigonométriques et les multiples de fonctions trigonométriques, pour les angles en degrés. De nombreuses règles à calcul ont leurs échelles S, T et ST marquées de degrés et de minutes. Les modèles dits "décitrig" utilisent plutôt des fractions décimales de degrés.

Logarithmes et exponentielles

Les logarithmes et les exponentielles en base 10 sont trouvés en utilisant l'échelle L, qui est linéaire. Certaines règles de calcul ont une échelle Ln, qui correspond à la base e.

L'échelle Ln a été inventée par un élève de 11e année, Stephen B. Cohen, en 1958. L'intention initiale était de permettre à l'utilisateur de sélectionner un exposant x (dans la gamme de 0 à 2,3) sur l'échelle Ln et de lire ^{ex sur l'échelle} C (ou D) et ^{e-x sur l'}échelle CI (ou DI). Pickett, Inc. s'est vu accorder des droits exclusifs sur l'échelle. Plus tard, l'inventeur a créé un ensemble de "marques" sur l'échelle Ln pour étendre la gamme au-delà de la limite de 2,3, mais Pickett n'a jamais incorporé ces marques sur aucune de ses règles à calcul. ^[]

Addition et soustraction

Les règles de calcul ne sont généralement pas utilisées pour l'addition et la soustraction, mais il est néanmoins possible de le faire en utilisant deux techniques différentes.

La première méthode pour effectuer l'addition et la soustraction sur les échelles C et D (ou toute autre échelle comparable) nécessite de convertir le problème en un problème de division. Pour l'addition, le quotient des deux variables plus une fois le diviseur est égal à leur somme :

x + y = ( x y + 1 ) y {\displaystyle x+y=\left({\frac {x}{y}}+1\right)y}

Pour la soustraction, le quotient des deux variables moins une fois le diviseur est égal à leur différence :

x - y = ( x y - 1 ) y [style d'affichage] x-y=\left({\frac {x}{y}}-1\right)y}

Cette méthode est similaire à la technique d'addition/soustraction utilisée pour les circuits électroniques à grande vitesse avec le système des nombres logarithmiques dans les applications informatiques spécialisées comme le superordinateur Gravity Pipe (GRAPE) et les modèles de Markov cachés.

La deuxième méthode utilise une échelle linéaire L mobile disponible sur certains modèles. L'addition et la soustraction sont effectuées en faisant glisser le curseur vers la gauche (pour la soustraction) ou vers la droite (pour l'addition) puis en ramenant le curseur à 0 pour lire le résultat.

Conception physique

Règles linéaires standard

La longueur de la règle à calcul est indiquée en fonction de la longueur nominale des échelles. Les échelles des modèles "10 pouces" les plus courants ont en fait une longueur de 25 cm, car elles ont été fabriquées selon des normes métriques, bien que certaines règles proposent des échelles légèrement allongées pour simplifier la manipulation lorsqu'un résultat déborde. Les règles de poche sont généralement de 5 pouces. Des modèles de quelques mètres de long ont été vendus pour être accrochés dans les salles de classe à des fins pédagogiques. [1]

Généralement, les divisions marquent une échelle avec une précision de deux chiffres significatifs, et l'utilisateur estime le troisième chiffre. Certaines règles à calcul haut de gamme sont dotées de curseurs grossissants qui rendent les marques plus faciles à voir. De tels curseurs peuvent effectivement doubler la précision des lectures, permettant à une règle à calcul de 10 pouces de servir aussi bien qu'à une règle à calcul de 20 pouces.

Diverses autres commodités ont été développées. Les échelles trigonométriques sont parfois doubles, en noir et rouge, avec des angles complémentaires, le style dit "Darmstadt". Les règles à calcul duplex reproduisent souvent certaines des échelles figurant au dos. Les échelles sont souvent "divisées" pour obtenir une plus grande précision.

Des règles de calcul spécialisées ont été inventées pour diverses formes d'ingénierie, de commerce et de banque. Ces règles comportaient souvent des calculs communs directement exprimés sous forme d'échelles spéciales, par exemple le calcul des prêts, les quantités optimales d'achat ou des équations d'ingénierie particulières. Par exemple, la société Fisher Controls a distribué une règle à calcul personnalisée adaptée à la résolution des équations utilisées pour sélectionner la taille appropriée des vannes de régulation du débit industriel. ^[]

Règles circulaires pour les diapositives

Les règles à calcul circulaires sont de deux types de base, l'une avec deux curseurs (à gauche), et l'autre avec un disque mobile et un seul curseur (à droite). Les versions à deux curseurs effectuent des multiplications et des divisions en maintenant un angle fixe entre les curseurs lorsqu'ils tournent autour du cadran. La version à curseur unique fonctionne davantage comme la règle à calcul standard grâce à l'alignement approprié des échelles.

L'avantage fondamental d'une règle à calcul circulaire est que la dimension la plus longue de l'outil a été réduite d'un facteur d'environ 3 (c'est-à-dire par π). Par exemple, l'échelle extérieure d'un cercle de 10 cm aurait une précision maximale égale à celle d'une règle à calcul ordinaire de 30 cm. Les règles circulaires éliminent également les calculs "hors échelle", car les échelles ont été conçues pour "s'enrouler" ; elles ne doivent jamais être réorientées lorsque les résultats sont proches de 1,0 - la règle est toujours à l'échelle. Cependant, pour les échelles non cycliques et non spirales comme les S, T et LL, la longueur de l'échelle est réduite pour faire place aux marges finales.

Les règles à calcul circulaires sont mécaniquement plus robustes et plus souples, mais la précision de l'alignement de leur échelle est sensible au centrage d'un pivot central ; un décalage de 0,1 mm du pivot peut entraîner une erreur d'alignement de 0,2 mm dans le pire des cas. Le pivot, cependant, empêche de rayer le visage et les curseurs. Les échelles les plus précises sont placées sur les anneaux extérieurs. Plutôt que des échelles "divisées", les règles circulaires haut de gamme utilisent des échelles en spirale pour les opérations plus complexes comme les échelles de log-of-log. Une règle circulaire haut de gamme de huit pouces avait une échelle logarithmique spiralée de 50 pouces.

Les principaux inconvénients des règles à calcul circulaires sont la difficulté à localiser les chiffres le long d'un disque rotatif et le nombre limité d'échelles. Un autre inconvénient des règles à calcul circulaires est que les échelles moins importantes sont plus proches du centre et ont une précision moindre. La plupart des étudiants ont appris à utiliser les règles à calcul sur les règles à calcul linéaires et n'ont pas trouvé de raison de changer.

L'une des règles de calcul encore utilisées quotidiennement dans le monde entier est la règle E6B. Il s'agit d'une règle à calcul circulaire créée dans les années 1930 pour les pilotes d'avion afin de les aider à calculer les temps morts. Grâce aux échelles imprimées sur le cadre, elle permet également d'effectuer diverses tâches telles que la conversion des valeurs de temps, de distance, de vitesse et de température, les erreurs de boussole et le calcul de la consommation de carburant. Le "moulin à prières" est toujours disponible dans les magasins de vol et reste largement utilisé. Si le GPS a réduit l'utilisation de l'estime pour la navigation aérienne et si les calculatrices portables ont repris un grand nombre de ses fonctions, le E6B reste largement utilisé comme appareil principal ou de secours et la majorité des écoles de pilotage exigent de leurs élèves une certaine maîtrise de ce système.

En 1952, la société horlogère suisse Breitling a lancé une montre-bracelet de pilote avec une règle à calcul circulaire intégrée, spécialisée dans les calculs de vol : la Breitling Navitimer. La règle circulaire Navitimer, appelée par Breitling "ordinateur de navigation", comportait des fonctions de vitesse, de taux/temps de montée/descente, de durée de vol, de distance et de consommation de carburant, ainsi que des fonctions de conversion de la quantité de carburant en kilomètres-milles nautiques et en gallons litres.

Matériel

Traditionnellement, les règles à calcul étaient fabriquées en bois dur comme l'acajou ou le buis avec des curseurs en verre et en métal. Au moins un instrument de haute précision était fabriqué en acier.

En 1895, une entreprise japonaise, Hemmi, a commencé à fabriquer des règles à calcul en bambou, qui avaient l'avantage d'être dimensionnellement stables, solides et naturellement autolubrifiantes. Ces règles à calcul en bambou ont été introduites en Suède en septembre 1933 [2], et probablement seulement un peu plus tôt en Allemagne. Les échelles étaient en celluloïd ou en plastique. Plus tard, les règles à calcul ont été fabriquées en plastique ou en aluminium peint avec du plastique. Plus tard, les curseurs étaient en acrylique ou en polycarbonate et glissaient sur des roulements en téflon.

Toutes les règles à calcul haut de gamme étaient gravées de chiffres et d'échelles, puis remplies de peinture ou d'une autre résine. Les règles peintes ou imprimées étaient considérées comme inférieures car les marquages pouvaient s'effacer. Néanmoins, Pickett, probablement l'entreprise de règles à calcul la plus prospère d'Amérique, fabriquait toutes les échelles imprimées. Les règles à calcul de qualité supérieure étaient munies de loquets astucieux pour éviter qu'elles ne s'effondrent par accident, et de pare-chocs pour protéger les balances et le curseur des frottements sur les plateaux de table. La méthode de nettoyage recommandée pour les marquages gravés est de frotter légèrement avec de la laine d'acier. Pour les règles à calcul peintes, et les malaises de cœur, utilisez du liquide de nettoyage pour vitres du commerce dilué et un chiffon doux.

Règle circulaire de Pickett avec deux curseurs. (10,9 cm de diamètre) L'inverse a une échelle supplémentaire et un curseur.


Une simple règle à calcul circulaire, fabriquée par Concise Co., Ltd. à Tokyo, au Japon, avec uniquement des échelles inverses, carrées et cubiques. Au verso se trouve une liste pratique de 38 facteurs de conversion métriques/impériaux.


Montre-bracelet Breitling Navitimer avec règle à calcul circulaire

Histoire

La règle à calcul a été inventée vers 1620-1630, peu après la publication du concept de logarithme par John Napier. Edmund Gunter, d'Oxford, a développé un appareil de calcul à échelle logarithmique unique, qui, avec des outils de mesure supplémentaires, pouvait être utilisé pour multiplier et diviser. La première description de cette échelle a été publiée à Paris en 1624 par Edmund Wingate (v. 1593 - 1656), un mathématicien anglais, dans un livre intitulé "L'usage de la règle de proportion en l'arithmétique & géométrie". Le livre contient une double échelle dont un côté est une échelle logarithmique et l'autre une échelle tabulaire. En 1630, William Oughtred de Cambridge a inventé une règle à calcul circulaire et en 1632, il a combiné deux règles de Gunter, tenues à la main, pour en faire un dispositif qui est reconnaissable à la règle à calcul moderne. Comme son contemporain de Cambridge, Isaac Newton, Oughtred a enseigné ses idées en privé à ses étudiants, mais a tardé à les publier, et comme Newton, il s'est impliqué dans une controverse vitriolique sur la priorité, avec son ancien élève Richard Delamain et les revendications de Wingate. Les idées d'Oughtred n'ont été rendues publiques que dans les publications de son élève William Forster en 1632 et 1653.

En 1677, Henry Coggeshall a créé une règle pliante de deux pieds pour mesurer le bois, appelée règle à calcul Coggeshall. Sa conception et ses utilisations de l'outil ont donné à la règle à calcul un but autre que la recherche mathématique.

En 1722, Warner a introduit les échelles de deux et trois décennies, et en 1755, Everard a inclus une échelle inversée ; une règle à calcul contenant toutes ces échelles est généralement connue sous le nom de règle "polyphasée".

En 1815, Peter Roget a inventé la règle à calcul du journal de bord, qui comprenait une échelle affichant le logarithme du logarithme. Cela permettait à l'utilisateur d'effectuer directement des calculs impliquant des racines et des exposants. Cette règle était particulièrement utile pour les puissances fractionnaires.

Une forme moderne

La forme la plus moderne a été créée en 1859 par le lieutenant d'artillerie français Amédée Mannheim, "qui a eu la chance de voir son règlement établi par une firme de réputation nationale et de le faire adopter par l'artillerie française". C'est à cette époque, alors que l'ingénierie devenait une activité professionnelle reconnue, que les règles à calcul ont été largement utilisées en Europe. Elles ne sont devenues courantes aux États-Unis qu'en 1881, lorsqu'Edwin Thacher y a introduit une règle cylindrique. La règle duplex a été inventée par William Cox en 1891, et a été produite par Keuffel and Esser Co. de New York.

Les travaux astronomiques nécessitaient également des calculs fins, et au 19ème siècle, en Allemagne, une règle à calcul en acier d'environ 2 mètres de long était utilisée dans un observatoire. Un microscope y était fixé, ce qui lui donnait une précision de six décimales.

Pendant la Seconde Guerre mondiale, les bombardiers et les navigateurs qui avaient besoin de calculs rapides utilisaient souvent des règles de calcul spécialisées. Un bureau de la marine américaine a en fait conçu un "châssis" de règle à calcul générique avec un corps en aluminium et un curseur en plastique dans lequel des cartes en celluloïd (imprimées des deux côtés) pouvaient être placées pour des calculs spéciaux. Le procédé a été inventé pour calculer la distance, la consommation de carburant et l'altitude des avions, puis adapté à de nombreuses autres fins.

Tout au long des années 1950 et 1960, la règle à calcul était le symbole de la profession d'ingénieur (de la même manière que le stéthoscope symbolise la profession médicale). ^{[] Le} spécialiste allemand des fusées, Wernher von Braun, a apporté avec lui deux règles à calcul Nestler des années 1930 lorsqu'il a déménagé aux États-Unis après la Seconde Guerre mondiale pour travailler sur le programme spatial américain. Tout au long de sa vie, il n'a jamais utilisé d'autres appareils de calcul de poche ; les règles à calcul lui ont parfaitement servi pour faire des estimations rapides des paramètres de conception des fusées et d'autres chiffres. Les règles à calcul en aluminium de la marque Pickett ont été utilisées lors de cinq missions spatiales Apollo, y compris vers la lune, selon la publicité sur les boîtes de règles à calcul N600 de Pickett [3].

Certains étudiants en ingénierie et ingénieurs transportaient des règles à calcul de dix pouces dans des étuis de ceinture, et même au milieu des années 1970, c'était un spectacle courant sur les campus. Les étudiants pouvaient également garder une règle de dix ou vingt pouces pour le travail de précision à la maison ou au bureau tout en transportant une règle de poche de cinq pouces.

En 2004, les chercheurs en éducation David B. Sher et Dean C. Nataro ont conçu un nouveau type de règle à calcul basée sur la prothèse, un algorithme de calcul rapide de produits antérieur aux logarithmes. Cependant, la construction d'une règle à calcul au-delà du prototype initial n'a suscité que peu d'intérêt pratique. [4]

Déclin

L'importance de la règle à calcul a commencé à diminuer à mesure que les ordinateurs électroniques, une ressource nouvelle mais très rare dans les années 1950, devenaient largement accessibles aux travailleurs techniques dans les années 1960. L'introduction de Fortran en 1957 a rendu les ordinateurs pratiques pour la résolution de problèmes mathématiques de taille modeste. IBM a introduit une série d'ordinateurs plus abordables, les IBM 650 (1954), IBM 1620 (1959), IBM 1130 (1965) destinés au marché des sciences et de l'ingénierie. Le langage de programmation BASIC de John Kemeny (1964) a permis aux étudiants d'utiliser facilement les ordinateurs. Le mini-ordinateur DEC PDP-8 a été introduit en 1965.

Les ordinateurs ont également changé la nature du calcul. Avec les règles à calcul, on mettait l'accent sur le travail de l'algèbre pour obtenir des expressions sous la forme la plus calculable possible. Les utilisateurs de règles à calcul se contentaient d'approximer ou de laisser tomber de petits termes pour simplifier le calcul. Le Fortran permettait de taper des formules compliquées dans les manuels sans avoir à les reformuler. L'intégration numérique était souvent plus facile que d'essayer de trouver des solutions de forme fermée pour des problèmes difficiles. Le jeune ingénieur demandant du temps à l'ordinateur pour résoudre un problème qui aurait pu être fait par quelques coups de règle à calcul est devenu un cliché humoristique. Dans de nombreux centres informatiques, une règle à calcul encadrée était accrochée au mur avec la mention "En cas d'urgence, cassez du verre".

Une autre étape vers le remplacement des règles à calcul par l'électronique a été le développement de calculatrices électroniques à usage scientifique et technique. La première comprenait la LOCI-2 des Laboratoires Wang, introduite en 1965, qui utilisait des logarithmes pour la multiplication et la division, et la HP-9100 de Hewlett-Packard, introduite en 1968. Le HP-9100 avait des fonctions trigonométriques (sin, cos, tan) en plus des exponentielles et des logarithmes. Elle utilisait l'algorithme CORDIC (ordinateur numérique de rotation des coordonnées), qui permet de calculer des fonctions trigonométriques en utilisant uniquement des opérations de décalage et d'addition. Cette méthode a facilité le développement de calculatrices scientifiques de plus en plus petites.

Le dernier clou dans le cercueil de la règle à calcul a été le lancement des calculatrices scientifiques de poche, dont la Hewlett-Packard HP-35 de 1972 a été la première. Ces calculatrices ont été appelées "règles à calcul" car elles pouvaient exécuter la plupart ou la totalité des fonctions d'une règle à calcul. À plusieurs centaines de dollars, même celle-ci était considérée comme coûteuse pour la plupart des étudiants. Si les règles à calcul professionnelles pouvaient également être assez chères, les pharmacies vendaient souvent des modèles de base en plastique pour moins de 20 dollars américains. Mais en 1975, les calculatrices électroniques à quatre fonctions de base pouvaient être achetées pour moins de 50 dollars. En 1976, la TI-30 proposait une calculatrice scientifique pour moins de 25 dollars. Après cette date, le marché des règles à calcul s'est rapidement tari, les petites calculatrices scientifiques devenant abordables.

William Oughtred (1575-1660), inventeur de la règle à calcul circulaire


Ingénieur utilisant une règle à calcul. Notez la calculatrice mécanique en arrière-plan.


TI-30

Avantages

• Une règle à calcul tend à modérer l'erreur de "fausse précision" et de signification. La précision typique dont dispose l'utilisateur d'une règle à calcul est d'environ trois endroits de précision. Cela correspond à la plupart des données disponibles pour la saisie de formules d'ingénierie. Lorsqu'une calculatrice de poche moderne est utilisée, la précision peut être affichée à sept décimales ou plus, alors qu'en réalité les résultats ne peuvent jamais être plus précis que les données d'entrée disponibles.
• Une règle à calcul nécessite une estimation continue de l'ordre de grandeur des résultats. Sur une règle à calcul, 1,5 × 30 (qui équivaut à 45) donnera le même résultat que 1 500 000 × 0,03 (qui équivaut à 45 000). Il appartient à l'ingénieur de déterminer en permanence le caractère raisonnable des résultats, ce qui peut être perdu lorsque les chiffres sont entrés par inadvertance dans un programme informatique ou une calculatrice.
• Lorsqu'on effectue une séquence de multiplications ou de divisions par le même nombre, la réponse peut souvent être déterminée en jetant simplement un coup d'œil à la règle à calcul sans aucune manipulation. Cela peut être particulièrement utile lors du calcul de pourcentages, par exemple pour les résultats d'un test, ou lors de la comparaison de prix, par exemple en dollars par kilogramme. Les calculs multiples de vitesse-temps-distance peuvent être effectués d'un seul coup d'œil en main avec une règle à calcul.
• Une règle à calcul ne dépend pas de l'électricité.
• Une règle à calcul est une technologie facile à reproduire. À partir d'un exemple donné de règle à calcul, un artisan compétent peut en construire d'autres à partir de matériaux rudimentaires en utilisant des procédés non industriels.
• Les règles de calcul sont très standardisées, il n'est donc pas nécessaire de réapprendre quoi que ce soit lorsque l'on passe à une autre règle.
• Les règles à calcul sont polyvalentes et peuvent être utilisées dans des situations et des environnements où un utilisateur humain pourrait avoir une dextérité réduite (par exemple, parce qu'il doit porter des gants de protection). Inversement, une calculatrice peut être difficile à utiliser dans de telles situations - une règle à calcul a peu de chances d'entraîner une erreur similaire à celle résultant d'une pression erronée sur le mauvais bouton d'une calculatrice.
• Les règles de défilement peuvent être en carton ou en papier. De nombreux tableaux gratuits ou appareils de calcul spécialisés en carton sont en fait des règles à calcul linéaires ou circulaires spécialisées.

L'un des avantages de l'utilisation d'une règle à calcul avec une calculatrice électronique est qu'un calcul important peut être vérifié en le faisant sur les deux ; les deux instruments étant si différents, il y a peu de chances de faire deux fois la même erreur.

Inconvénients

• Des erreurs peuvent résulter d'une imprécision mécanique.
• Les calculs utilisant la règle à calcul sont d'une précision limitée en raison de leurs entrées et sorties analogiques. À l'inverse, en raison de l'entrée numérique discrète et des opérations électroniques en virgule flottante, même les modestes calculatrices modernes ont des résolutions de sortie d'au moins six chiffres significatifs.

Pages connexes

• Abacus
• Logarithme