Ensemble

Notation

La plupart des mathématiciens utilisent des lettres majuscules italiques (généralement romaines) pour écrire sur les ensembles. Les choses qui sont considérées comme des éléments d'ensembles sont généralement écrites avec des lettres romaines minuscules.

Une façon de montrer un ensemble est de présenter une liste de ses membres, séparés par des virgules, entre crochets. Par exemple,

• X={1,2,3} est fixé qui a les membres 1, 2 et 3.

Un autre moyen est de dire ce qui est vrai des membres de l'ensemble, comme ceci :

• {x | x est un nombre naturel & x < 4}.

C'est-à-dire en anglais parlé : "l'ensemble de tous les x tels que x est un nombre naturel et x est inférieur à quatre".

L'ensemble vide est écrit d'une manière particulière :

• ∅ {\displaystyle \emptyset }

Lorsque l'objet a est le membre de l'ensemble A, il est écrit comme :

• a ∈ A.

C'est-à-dire en anglais parlé : "a est un membre de A"

Que faire des décors ?

Élément de

Diverses choses peuvent être mises dans un sac. Plus tard, on peut se demander si une certaine chose se trouve dans le sac. Les mathématiciens appellent cet élément de. Une chose est un élément d'un ensemble, si cette chose se trouve dans le sac respectif. Le symbole utilisé pour cela est ∈ {\displaystyle \in }

a ∈ A {\displaystyle a\in \mathbf {A} }

signifie qu'un affichage de type a est dans le sac A }

Ensemble vide

Comme un sac, un ensemble peut aussi être vide. L'ensemble vide est comme un sac vide : il ne contient rien.

Comparaison des ensembles

Deux ensembles peuvent être comparés. C'est comme si on regardait deux sacs différents. S'ils contiennent les mêmes choses, ils sont égaux.

La cardinalité d'un ensemble

Lorsque les mathématiciens parlent d'un ensemble, ils veulent parfois savoir quelle est la taille d'un ensemble. Pour ce faire, ils comptent le nombre d'éléments qui composent l'ensemble (combien d'éléments se trouvent dans le sac). La cardinalité peut être un simple nombre. L'ensemble vide a une cardinalité de 0. L'ensemble { a p p l e , o r a n g e } a une cardinalité de 2.

Deux ensembles ont la même cardinalité si nous pouvons apparier leurs éléments - si nous pouvons joindre deux éléments, un de chaque ensemble. L'ensemble { a p p l e , o r a n g e } et l'ensemble ont la même cardinalité. On peut associer une pomme avec le soleil, et une orange avec la lune. L'ordre n'a pas d'importance. Il est possible d'apparier les éléments, et aucun n'est laissé de côté. Mais l'ensemble { d o g , c a t , b i r d } et l'ensemble { 5 , 6 } {\displaystyle \{5,6}} ont une cardinalité différente. Si on essaie de les associer, on oublie toujours un animal.

Une cardinalité infinie

Parfois, la cardinalité n'est pas un chiffre. Parfois, un ensemble a une cardinalité infinie. L'ensemble des nombres entiers est un ensemble à cardinalité infinie. Certains ensembles à cardinalité infinie sont plus grands (ont une cardinalité plus grande) que d'autres. Par exemple, il y a plus de nombres réels que de nombres naturels. Cela signifie que nous ne pouvons pas apparier l'ensemble des entiers et l'ensemble des nombres réels, même si nous avons travaillé à l'infini. Si un ensemble a la même cardinalité que l'ensemble d'entiers, il est appelé ensemble dénombrable. Mais si un ensemble a la même cardinalité que les nombres réels, il est appelé un ensemble non dénombrable.

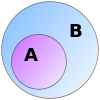
Sous-ensembles

Si vous regardez l'ensemble {a,b} et l'ensemble {a,b,c,d}, vous pouvez voir que tous les éléments du premier ensemble se trouvent également dans le second ensemble.
Nous disons : {a,b} est un sous-ensemble de {a,b,c,d} En tant que
 formule, il ressemble à ceci :
{a,b} ⊆ { a , b , c , d } {\displaystyle \{a,b\}\subseteq \{a,b,c,d\}}

Lorsque tous les éléments de A sont également des éléments de B, nous appelons A un sous-ensemble de B :
A ⊆ B {\displaystyle A\subseteq B}
 On lit généralement "A est contenu dans B"

Exemple :
 chaque Chevrolet est une voiture américaine. Le jeu de toutes les Chevrolet est donc contenu dans le jeu de toutes les voitures américaines.

Opérations fixes

Il existe différentes façons de combiner les ensembles.

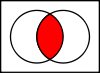
Intersections

L'intersection A ∩ B {\displaystyle A\cap B} de deux ensembles A et B est un ensemble qui contient tous les éléments, qui
 sont à la fois dans l'ensemble A et dans l'ensemble B.
 Quand A est l'ensemble de toutes les voitures bon marché, et B est l'ensemble de toutes les voitures américaines,
 alors A ∩ B {\displaystyle A\cap B} est l'ensemble de toutes les voitures américaines bon marché.

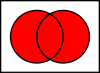
Syndicats

L'union A ∪ B {\displaystyle A\cup B} de deux ensembles A et B est un ensemble qui contient tous les éléments,
 qui sont dans l'ensemble A ou dans l'ensemble B.

Ce "ou" est la disjonction inclusive, de sorte que l'union contient également les éléments qui se trouvent dans le jeu A et dans le jeu B.

Au fait : Cela signifie que l'intersection est un sous-ensemble de l'union :

( A ∩ B ) ⊆ ( A ∪ B ) {\displaystyle (A\cap B)\subseteq (A\cup B)}

Lorsque A est l'ensemble de toutes les voitures bon marché, et B l'ensemble de toutes les voitures américaines,
 alors A ∪ B {\displaystyle A\cup B}est l'ensemble de toutes les voitures, sans les voitures chères qui ne sont pas américaines.

Compléments

La complémentarité peut signifier deux choses différentes :

• Le complément de A est l'univers U sans tous les éléments de A :

A C = U ∖ A {\displaystyle A^{\rm {C}}}=U\setminus A} L'univers U est l'ensemble de toutes les choses dont vous parlez.
Quand U est l'ensemble de toutes les voitures, et A l'ensemble de toutes les voitures bon marché,
 alors ^{AC est l'ensemble de toutes les} voitures chères.

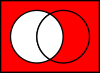
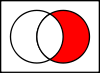
• Le complément relatif de A dans B est l'ensemble B sans tous les éléments de A :

B ∖ A {\displaystyle B\setminus A} C'est ce qu'
on appelle souvent la différence fixe.
Lorsque A est l'ensemble de toutes les voitures bon marché, et B l'ensemble de toutes les voitures américaines,
 alors B ∖ A {\displaystyle B\setminus A} est l'ensemble de toutes les voitures américaines chères.

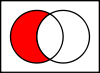
Si vous échangez les ensembles dans la différence d'ensemble, le résultat est différent :
 dans l'exemple avec les voitures, la différence A ∖ B {\displaystyle A\setminus B} est l'ensemble de toutes les voitures bon marché, qui ne sont pas fabriquées en Amérique.

Ensembles spéciaux

Certains ensembles sont très importants pour les mathématiques. Ils sont utilisés très souvent. L'un d'entre eux est l'ensemble vide. Beaucoup de ces ensembles sont écrits en caractères gras au tableau noir, comme indiqué ci-dessous. Les ensembles spéciaux comprennent :

• P {\displaystyle \mathbb {P} } désignant l'ensemble de tous les nombres premiers.
• N {\displaystyle \mathbb {N} } désignant l'ensemble des nombres naturels. C'est-à-dire, N {\displaystyle \mathbb {N} } = {1, 2, 3, ...}, ou parfois N {\displaystyle \mathbb {N} } = {0, 1, 2, 3, ...}.
• Z {\displaystyle \mathbb {Z} } désignant l'ensemble de tous les entiers (qu'ils soient positifs, négatifs ou nuls). Donc, Z {\displaystyle \mathbb {Z} } = {..., -2, -1, 0, 1, 2, ...}.
• Q {\displaystyle \mathbb {Q} } qui désigne l'ensemble de tous les nombres rationnels (c'est-à-dire l'ensemble de toutes les fractions propres et impropres). Donc, Q = { a b : a , b ∈ Z , b ≠ 0 } {\displaystyle \mathbb {Q} =\left\{\begin{\begin{\b}{\frac {a}{b}}\end{\batrix}}:a,b\in \mathbb {Z} ,b\neq 0\right\}} c'est-à-dire toutes les fractions a b {matrice}{\frac {a}{b}} {matrice}}} où a et b sont dans l'ensemble de tous les entiers et b n'est pas égal à 0. Par exemple, 1 4 ∈ Q {matrice}{\frac {1}{4}} {matrice}} {fin{matrice}} {in \mathbb {Q} } and 11 6 ∈ Q {\displaystyle {\begin{matrix}{\frac {11}{6}}\end{matrix}}\in \mathbb {Q} } . Tous les entiers sont dans cet ensemble puisque chaque entier a peut être exprimé sous la forme d'une fraction a 1 {\début{matrice}{\frac {a}{1}}\fin{matrice}}}. .
• R {\displaystyle \mathbb {R} } qui désigne l'ensemble de tous les nombres réels. Cet ensemble comprend tous les nombres rationnels, ainsi que tous les nombres irrationnels (c'est-à-dire les nombres qui ne peuvent pas être réécrits sous forme de fractions, tels que π , {\displaystyle \pi ,} e , {\displaystyle e,} et √2).
• C {\displaystyle \mathbb {C} } qui désigne l'ensemble de tous les nombres complexes.

Chacun de ces ensembles de nombres comporte un nombre infini d'éléments, et P ⊂ N ⊂ Z ⊂ Q ⊂ R ⊂ C {\displaystyle \mathbb {P} \subset \mathbb {N} \subset \mathbb {Z} \subset \mathbb {Q} \subset \mathbb {R} \subset \mathbb {C} } . Les nombres premiers sont utilisés moins fréquemment que les autres en dehors de la théorie des nombres et des domaines connexes.

Paradoxes sur les décors

Le mathématicien Bertrand Russell a constaté que cette théorie des ensembles pose des problèmes. Il l'a affirmé dans un paradoxe appelé le paradoxe de Russell. Une version plus facile à comprendre, plus proche de la vie réelle, est appelée le paradoxe de Barber :

Le paradoxe du barbier

Il y a une petite ville quelque part. Dans cette ville, il y a un barbier. Tous les hommes de la ville n'aiment pas la barbe, alors soit ils se rasent eux-mêmes, soit ils vont chez le barbier pour se faire raser par le barbier.

Nous pouvons donc faire une déclaration sur le barbier lui-même : Le barbier rase tous les hommes qui ne se rasent pas. Il ne rase que ces hommes (puisque les autres se rasent eux-mêmes et n'ont pas besoin d'un barbier pour les raser).

Cela soulève bien sûr la question : Que fait le barbier chaque matin pour avoir l'air bien rasé ? C'est là le paradoxe.

• Si le barbier ne se rase pas, il suivra la règle et se rasera lui-même (allez chez le barbier pour vous faire raser)
• Si le barbier se rase effectivement, il ne se rasera pas, selon la règle donnée ci-dessus.