Mécanique quantique
La mécanique quantique ou QM, décrit comment l'Univers fonctionne au niveau plus petit que les atomes. Elle est également appelée "physique quantique" ou "théorie quantique". Quantum est le mot latin pour "combien", et la mécanique est le domaine de la science qui s'intéresse au mouvement. Un quantum d'énergie est une quantité spécifique d'énergie, et la mécanique quantique décrit comment cette énergie se déplace et interagit au niveau subatomique.
Les atomes étaient autrefois considérés comme les plus petits éléments constitutifs de la matière, mais la science moderne a montré qu'il existe des particules encore plus petites, comme les protons, les neutrons et les électrons. La MQ est la partie de la physique qui décrit le fonctionnement des particules qui composent les atomes.
QM nous dit aussi comment fonctionnent les ondes électromagnétiques (comme la lumière). Une grande partie de la physique et de la chimie modernes peut être décrite et comprise en utilisant les règles mathématiques de la mécanique quantique.
Les mathématiques utilisées pour étudier les particules subatomiques et les ondes électromagnétiques sont très complexes car elles agissent de manière très étrange.
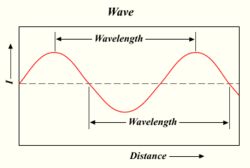
La longueur d'onde d'une onde de lumière
Ondes et photons
Les photons sont des particules beaucoup plus petites que les atomes, les protons et les électrons ; en fait, ils n'ont pas de masse du tout. Les photons sont comme des "paquets" ou des paquets d'énergie. Les sources de lumière telles que les bougies ou les lasers émettent de la lumière en bits appelés photons.
Plus une lampe émet de photons, plus la lumière est intense. La lumière est une forme d'énergie qui se comporte comme les ondes dans l'eau ou les ondes radio. La distance entre le sommet d'une onde et le sommet de l'onde suivante est appelée "longueur d'onde". Chaque photon transporte une certaine quantité, ou "quantum", d'énergie en fonction de sa longueur d'onde.
La couleur d'une lumière dépend de sa longueur d'onde. Le violet (la couleur la plus profonde de l'arc-en-ciel) a une longueur d'onde d'environ 400 nm ("nanomètres"), soit 0,00004 centimètre ou 0,000016 pouce. Les photons ayant une longueur d'onde de 10-400 nm sont appelés lumière ultraviolette (ou UV). Cette lumière ne peut pas être vue par l'œil humain. À l'autre extrémité du spectre, la lumière rouge est d'environ 700 nm. La lumière infrarouge est d'environ 700 nm à 300 000 nm. L'œil humain n'est pas non plus sensible à la lumière infrarouge.
Les longueurs d'onde ne sont pas toujours aussi petites. Les ondes radio ont des longueurs d'onde plus importantes. Les longueurs d'onde d'une radio FM peuvent atteindre plusieurs mètres de long (par exemple, les stations émettant sur 99,5 FM émettent de l'énergie radio d'une longueur d'onde d'environ 3 mètres, soit environ 3 mètres). Chaque photon a une certaine quantité d'énergie liée à sa longueur d'onde. Plus la longueur d'onde d'un photon est courte, plus son énergie est importante. Par exemple, un photon ultraviolet a plus d'énergie qu'un photon infrarouge.
La longueur d'onde et la fréquence (le nombre de fois que l'onde atteint sa crête par seconde) sont inversement proportionnelles, ce qui signifie qu'une longueur d'onde plus grande aura une fréquence plus basse, et vice versa. Si la couleur de la lumière est infrarouge (de fréquence inférieure à celle de la lumière rouge), chaque photon peut chauffer ce qu'il frappe. Ainsi, si une forte lampe infrarouge (une lampe chauffante) est pointée sur une personne, cette personne aura chaud, ou même très chaud, en raison de l'énergie stockée dans les nombreux photons. La surface de la lampe infrarouge peut même devenir assez chaude pour brûler une personne qui pourrait la toucher. Les humains ne peuvent pas voir la lumière infrarouge, mais nous pouvons sentir le rayonnement sous forme de chaleur. Par exemple, une personne passant devant un bâtiment en briques chauffé par le soleil ressentira la chaleur du bâtiment sans avoir à le toucher.
Les formulations mathématiques de la mécanique quantique sont abstraites. Une fonction mathématique, appelée fonction d'onde, fournit des informations sur l'amplitude de probabilité (le carré de l'amplitude de probabilité est la probabilité) de la position, du moment et d'autres propriétés physiques d'une particule. De nombreux résultats de la mécanique quantique ne sont pas facilement visualisables en termes de mécanique classique.
La lumière ultraviolette est plus fréquente que la lumière violette, de sorte qu'elle ne se trouve même pas dans le domaine de la lumière visible. Chaque photon dans la gamme des ultraviolets a beaucoup d'énergie, suffisamment pour blesser les cellules de la peau et provoquer un coup de soleil. En fait, la plupart des formes de coups de soleil ne sont pas causées par la chaleur ; elles sont dues à la forte énergie des rayons UV du soleil qui endommagent les cellules de votre peau. Même les fréquences les plus élevées de la lumière (ou du rayonnement électromagnétique) peuvent pénétrer plus profondément dans le corps et causer encore plus de dommages. Les rayons X ont une telle énergie qu'ils peuvent pénétrer profondément dans le corps humain et tuer des cellules. Les humains ne peuvent pas voir ou sentir la lumière ultraviolette ou les rayons X. Ils peuvent seulement savoir qu'ils ont été sous une lumière à si haute fréquence lorsqu'ils subissent une brûlure par irradiation. Les zones où il est important de tuer les germes utilisent souvent des lampes à ultraviolets pour détruire les bactéries, les champignons, etc. Les rayons X sont parfois utilisés pour tuer les cellules cancéreuses.
La mécanique quantique a vu le jour lorsqu'on a découvert qu'une certaine fréquence signifie une certaine quantité d'énergie. L'énergie est proportionnelle à la fréquence (E ∝ f). Plus la fréquence est élevée, plus un photon a d'énergie et plus il peut causer de dommages. La mécanique quantique s'est ensuite développée pour expliquer la structure interne des atomes. La mécanique quantique explique également la façon dont un photon peut interférer avec lui-même, et bien d'autres choses encore jamais imaginées en physique classique.

Le noir à gauche est un ultraviolet (haute fréquence) ; le noir à droite est un infrarouge (basse fréquence).
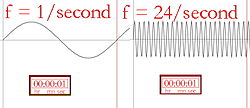
Description picturale de la fréquence
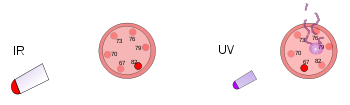
À gauche, un thermomètre en plastique est placé sous une lampe à chaleur vive. Ce rayonnement infrarouge réchauffe mais n'endommage pas le thermomètre. À droite, un autre thermomètre en plastique est frappé par une lumière ultraviolette de faible intensité. Ce rayonnement endommage le thermomètre, mais ne le réchauffe pas.
Quantification
Max Planck a découvert la relation entre la fréquence et l'énergie. Personne auparavant n'avait jamais deviné que la fréquence est directement proportionnelle à l'énergie (ce qui signifie que lorsque l'une d'elles double, l'autre le fait aussi). Sous ce qu'on appelle les unités naturelles, alors le nombre représentant la fréquence d'un photon représenterait aussi son énergie. L'équation serait alors la suivante :
E = f
ce qui signifie que l'énergie est égale à la fréquence.
Mais à mesure que la physique se développait, il n'y avait pas de lien naturel entre les unités utilisées pour mesurer l'énergie et les unités couramment utilisées pour mesurer le temps (et donc la fréquence). La formule que Planck a élaborée pour faire ressortir les chiffres était donc la bonne :
E = h × f
ou, l'énergie est égale à h fois la fréquence. Ce h est un nombre appelé constante de Planck d'après son découvreur.
La mécanique quantique est basée sur la connaissance qu'un photon d'une certaine fréquence signifie un photon d'une certaine quantité d'énergie. Outre cette relation, un type d'atome spécifique ne peut émettre que certaines fréquences de rayonnement, donc il ne peut également émettre que des photons ayant une certaine quantité d'énergie.
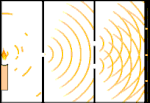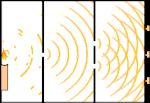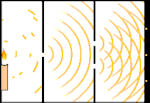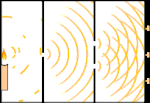
Expérience à double fente : la lumière passe de la source lumineuse à gauche aux franges (marquées dans le bord noir) à droite.
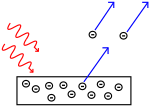
Effet photoélectrique : les photons frappent le métal et les électrons sont repoussés.
Histoire
Isaac Newton pensait que la lumière était faite de très petites choses que nous appellerions désormais des particules (il les appelait "corpuscules"). Christiaan Huygens pensait que la lumière était faite d'ondes. Les scientifiques pensaient qu'une chose ne pouvait pas être à la fois une particule et une onde.
Les scientifiques ont fait des expériences pour savoir si la lumière était faite de particules ou d'ondes. Ils ont découvert que les deux idées étaient justes - la lumière était en quelque sorte à la fois des ondes et des particules. L'expérience à double fente réalisée par Thomas Young a montré que la lumière doit agir comme une onde. L'effet photoélectrique découvert par Albert Einstein a prouvé que la lumière devait agir comme des particules qui transportaient des quantités spécifiques d'énergie, et que les énergies étaient liées à leurs fréquences. Ce résultat expérimental est appelé la "dualité onde-particule" en mécanique quantique. Plus tard, les physiciens ont découvert que tout se comporte à la fois comme une onde et comme une particule, et pas seulement la lumière. Cependant, cet effet est beaucoup plus faible dans les grands objets.
Voici quelques-unes des personnes qui ont découvert les éléments de base de la mécanique quantique : Max Planck, Albert Einstein, Satyendra Nath Bose, Niels Bohr, Louis de Broglie, Max Born, Paul Dirac, Werner Heisenberg, Wolfgang Pauli, Erwin Schrödinger, John von Neumann et Richard Feynman. Ils ont fait leur travail dans la première moitié du 20e siècle.

De gauche à droite : Max Planck, Albert Einstein, Niels Bohr, Louis de Broglie, Max Born, Paul Dirac, Werner Heisenberg, Wolfgang Pauli, Erwin Schrödinger, Richard Feynman
Au-delà de Planck
Les formules et les idées de la mécanique quantique ont été conçues pour expliquer la lumière qui provient de l'hydrogène incandescent. La théorie quantique de l'atome devait également expliquer pourquoi l'électron reste sur son orbite, ce que d'autres idées n'ont pas pu expliquer. Elle s'inspirait des idées plus anciennes selon lesquelles l'électron devrait tomber au centre de l'atome parce qu'il commence à être maintenu en orbite par sa propre énergie, mais qu'il perdrait rapidement son énergie en tournant sur son orbite. (En effet, on savait que les électrons et autres particules chargées émettaient de la lumière et perdaient de l'énergie lorsqu'ils changeaient de vitesse ou tournaient).
Les lampes à hydrogène fonctionnent comme les néons, mais les néons ont leur propre groupe de couleurs (et fréquences) de lumière. Les scientifiques ont appris qu'ils pouvaient identifier tous les éléments par les couleurs de la lumière qu'ils produisent. Ils n'arrivaient tout simplement pas à comprendre comment les fréquences étaient déterminées.
Ensuite, un mathématicien suisse du nom de Johann Balmer a trouvé une équation qui permet de dire ce que serait λ (lambda, pour la longueur d'onde) :
λ = B ( n 2 n 2 - 4 ) n = 3 , 4 , 5 , 6 {\displaystyle \lambda =B\left({\frac {n^{2}}{n^{2}-4}}\right)\qquad \qquad n=3,4,5,6}
où B est un nombre que Balmer a déterminé comme étant égal à 364,56 nm.
Cette équation ne fonctionnait que pour la lumière visible d'une lampe à hydrogène. Mais par la suite, l'équation a été rendue plus générale :
1 λ = R ( 1 m 2 - 1 n 2 ) , {\displaystyle {\frac {1}{\lambda }}=R\left({\frac {1}{m^{2}}}-{\frac {1}{n^{2}}}\right),}
où R est la constante de Rydberg, égale à 0,0110 nm-1, et n doit être supérieur à m.
Si l'on additionne les nombres m et n, il est facile de prédire les fréquences de nombreux types de lumière (ultraviolets, visibles et infrarouges). Pour voir comment cela fonctionne, allez à Hyperphysics et passez au milieu de la page. (Utilisez H = 1 pour l'hydrogène).
En 1908, Walter Ritz a mis au point le principe de combinaison Ritz qui montre comment certains écarts entre les fréquences se répètent sans cesse. Ce principe s'est avéré important pour Werner Heisenberg quelques années plus tard.
En 1905, Albert Einstein a utilisé l'idée de Planck pour montrer qu'un faisceau de lumière est constitué d'un flux de particules appelées photons. L'énergie de chaque photon dépend de sa fréquence. L'idée d'Einstein est le début de l'idée en mécanique quantique que toutes les particules subatomiques comme les électrons, les protons, les neutrons et autres sont à la fois des ondes et des particules. (Voir l'image de l'atome avec l'électron comme ondes à l'atome.) Cela a conduit à une théorie sur les particules subatomiques et les ondes électromagnétiques appelée dualité onde-particule. C'est là que les particules et les ondes n'étaient ni l'une ni l'autre, mais avaient certaines propriétés des deux.
En 1913, Niels Bohr a eu l'idée que les électrons ne pouvaient prendre que certaines orbites autour du noyau d'un atome. Selon la théorie de Bohr, les nombres appelés m et n dans l'équation ci-dessus pourraient représenter des orbites. Selon la théorie de Bohr, les électrons pourraient commencer dans une orbite m et finir dans une orbite n, ou un électron pourrait commencer dans une orbite n et finir dans une orbite m. Ainsi, si un photon frappe un électron, son énergie sera absorbée et l'électron se déplacera vers une orbite plus élevée en raison de cette énergie supplémentaire. Selon la théorie de Bohr, si un électron passe d'une orbite supérieure à une orbite inférieure, il devra alors renoncer à son énergie sous la forme d'un photon. L'énergie du photon sera égale à la différence d'énergie entre les deux orbites, et l'énergie d'un photon lui donne une certaine fréquence et une certaine couleur. La théorie de Bohr a fourni une bonne explication de nombreux aspects des phénomènes subatomiques, mais elle n'a pas réussi à expliquer pourquoi chacune des couleurs de la lumière produite par l'hydrogène incandescent (et par le néon incandescent ou tout autre élément) a une luminosité propre, et les différences de luminosité sont toujours les mêmes pour chaque élément.
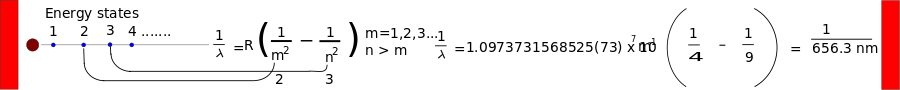
Au moment où Niels Bohr a présenté sa théorie, la plupart des choses sur la lumière produite par une lampe à hydrogène étaient connues, mais les scientifiques ne pouvaient toujours pas expliquer la luminosité de chacune des lignes produites par l'hydrogène incandescent.
Werner Heisenberg s'est chargé d'expliquer la luminosité ou "l'intensité" de chaque ligne. Il ne pouvait utiliser aucune règle simple comme celle que Balmer avait élaborée. Il a dû utiliser les mathématiques très difficiles de la physique classique qui permettent de tout calculer en termes de choses comme la masse (poids) d'un électron, la charge (force électrique statique) d'un électron et d'autres quantités infimes. La physique classique avait déjà des réponses pour la luminosité des bandes de couleur que produit une lampe à hydrogène, mais la théorie classique disait qu'il devait y avoir un arc-en-ciel continu, et non quatre bandes de couleur séparées. L'explication d'Heisenberg est la suivante :
Il existe une loi qui précise les fréquences de la lumière qui brille de l'hydrogène. Elle doit prédire les fréquences d'espacement lorsque les électrons impliqués se déplacent entre des orbites proches du noyau (centre) de l'atome, mais elle doit également prédire que les fréquences se rapprocheront de plus en plus l'une de l'autre à mesure que nous observerons ce que fait l'électron en se déplaçant entre des orbites de plus en plus éloignées. Il devra également prédire que les différences d'intensité entre les fréquences se rapprochent de plus en plus au fur et à mesure que nous nous éloignons. Là où la physique classique donne déjà les bonnes réponses par un ensemble d'équations, la nouvelle physique doit donner les mêmes réponses mais par des équations différentes.
La physique classique utilise les méthodes du mathématicien français Fourier pour faire une image mathématique du monde physique, et elle utilise des collections de courbes lisses qui vont ensemble pour faire une courbe lisse qui donne, dans ce cas, des intensités pour la lumière de toutes les fréquences à partir d'une certaine lumière. Mais ce n'est pas juste, car cette courbe lisse n'apparaît qu'aux fréquences les plus élevées. Aux fréquences plus basses, il y a toujours des points isolés et rien ne relie les points. Donc, pour faire une carte du monde réel, Heisenberg a dû faire un grand changement. Il a dû faire quelque chose pour ne retenir que les chiffres qui correspondraient à ce que l'on voit dans la nature. On dit parfois qu'il a "deviné" ces équations, mais il ne faisait pas de suppositions aveugles. Il a trouvé ce dont il avait besoin. Les chiffres qu'il a calculés ont permis de mettre des points sur un graphique, mais il n'y a pas eu de ligne tracée entre les points. Et faire un "graphe" uniquement avec des points pour chaque série de calculs aurait fait perdre beaucoup de papier et n'aurait rien donné. Heisenberg a trouvé un moyen de prédire efficacement les intensités pour différentes fréquences et d'organiser ces informations de manière utile.
En utilisant simplement la règle empirique donnée ci-dessus, celle que Balmer a mise en place et que Rydberg a améliorée, nous pouvons voir comment obtenir un ensemble de chiffres qui aiderait Heisenberg à obtenir le type d'image qu'il voulait :
La règle dit que lorsque l'électron passe d'une orbite à l'autre, il gagne ou perd de l'énergie, selon qu'il s'éloigne ou se rapproche du centre. On peut donc placer ces orbites ou ces niveaux d'énergie sous forme de titres en haut et sur le côté d'une grille. Pour des raisons historiques, l'orbite la plus basse est appelée n, et l'orbite suivante est appelée n - a, puis vient n - b, et ainsi de suite. Il est déroutant de constater qu'ils ont utilisé des nombres négatifs alors que les électrons gagnaient en fait de l'énergie, mais c'est bien ainsi.
Puisque la règle de Rydberg nous donne des fréquences, nous pouvons utiliser cette règle pour mettre des nombres en fonction de l'endroit où va l'électron. Si l'électron commence à n et finit à n, alors il n'est pas vraiment allé quelque part, donc il n'a pas gagné d'énergie et il n'en a pas perdu. La fréquence est donc de 0. Si l'électron commence à n-a et finit à n, alors il est passé d'une orbite supérieure à une orbite inférieure. Dans ce cas, il perd de l'énergie, et l'énergie qu'il perd se présente sous la forme d'un photon. Le photon a une certaine quantité d'énergie, e, et cela est lié à une certaine fréquence f par l'équation e = h f. Nous savons donc qu'un certain changement d'orbite va produire une certaine fréquence de lumière, f. Si l'électron commence à n et finit à n - a, cela signifie qu'il est passé d'une orbite inférieure à une orbite supérieure. Cela ne se produit que lorsqu'un photon d'une certaine fréquence et d'une certaine énergie arrive de l'extérieur, est absorbé par l'électron et lui donne son énergie, et c'est ce qui fait que l'électron sort vers une orbite plus élevée. Donc, pour que tout ait un sens, nous écrivons cette fréquence comme un nombre négatif. Il y avait un photon avec une certaine fréquence et maintenant il a été enlevé.
On peut donc faire une grille comme celle-ci, où f(a←b) signifie la fréquence impliquée lorsqu'un électron passe de l'état d'énergie (orbite) b à l'état d'énergie a (Là encore, les séquences sont rétrospectives, mais c'est ainsi qu'elles ont été écrites à l'origine) :
Grille de f
| États d'électrons | n | n-a | n-b | n-c | .... | |
| n | f(n←n) | f(n←n-a) | f(n←n-b) | f(n←n-c) | ..... | |
| n-a | f(n-a←n) | f(n-a←n-a) | f(n-a←n-b) | f(n-a←n-c) | ..... | |
| n-b | f(n-b←n) | f(n-b←n-a) | f(n-b←n-b) | f(n-b←n-c) | ..... | |
| transition.... | ..... | ..... | ..... | ..... |
Heisenberg n'a pas fait les grilles comme cela. Il a juste fait le calcul qui lui permettrait d'obtenir les intensités qu'il recherchait. Mais pour ce faire, il a dû multiplier deux amplitudes (la hauteur d'une onde) pour calculer l'intensité. (En physique classique, l'intensité est égale à l'amplitude au carré.) Il a fait une équation étrange pour résoudre ce problème, a rédigé le reste de son papier, l'a remis à son patron et est parti en vacances. Le Dr. Born a regardé sa drôle d'équation et elle lui a paru un peu folle. Il a dû se demander : "Pourquoi Heisenberg m'a-t-il donné cette chose étrange ? Pourquoi doit-il le faire de cette façon ?" Puis il a réalisé qu'il cherchait un plan pour quelque chose qu'il connaissait déjà très bien. Il avait l'habitude d'appeler la grille ou le tableau que nous pouvions écrire en faisant, par exemple, tous les calculs pour les fréquences, une matrice. Et l'étrange équation d'Heisenberg était une règle pour multiplier deux d'entre elles ensemble. Max Born était un très, très bon mathématicien. Il savait que puisque les deux matrices (grilles) multipliées représentent des choses différentes (comme la position (x,y,z) et la quantité de mouvement (mv), par exemple), alors quand vous multipliez la première matrice par la seconde, vous obtenez une réponse et quand vous multipliez la seconde matrice par la première, vous obtenez une autre réponse. Même s'il ne connaissait pas les matrices mathématiques, Heisenberg voyait déjà ce problème de "réponses différentes" et cela l'avait dérangé. Mais le Dr. Born était un si bon mathématicien qu'il a vu que la différence entre la première multiplication de la matrice et la deuxième multiplication de la matrice allait toujours impliquer la constante de Planck, h, multipliée par la racine carrée de l'unité négative, i. Donc, quelques jours après la découverte de Heisenberg, ils avaient déjà les bases mathématiques de ce que Heisenberg aimait appeler le "principe d'indétermination". Par "indéterminé", Heisenberg voulait dire que quelque chose comme un électron n'est pas immobilisé tant qu'il n'est pas immobilisé. C'est un peu comme une méduse qui est toujours en train de s'écraser et qui ne peut pas être "à un endroit" à moins que vous ne la tuiez. Plus tard, les gens ont pris l'habitude de l'appeler "le principe d'incertitude d'Heisenberg", ce qui a fait commettre à beaucoup l'erreur de penser que les électrons et les choses de ce genre sont vraiment "quelque part" mais que nous en sommes simplement incertains dans notre propre esprit. Cette idée est fausse. Ce n'est pas ce dont Heisenberg parlait. Avoir du mal à mesurer quelque chose est un problème, mais ce n'est pas le problème dont Heisenberg parlait.
L'idée d'Heisenberg est très difficile à saisir, mais nous pouvons la rendre plus claire avec un exemple. Tout d'abord, nous commencerons à appeler ces grilles "matrices", car nous devrons bientôt parler de multiplication des matrices.
Supposons que nous commencions avec deux types de mesures, la position (q) et l'élan (p). En 1925, Heisenberg a écrit une équation comme celle-ci :
Y ( n , n - b ) = ∑ a p ( n , n - a ) q ( n - a , n - b ) {\displaystyle Y(n,n-b)=\sum _{a}^{}\,p(n,n-a)q(n-a,n-b)}
Il ne le savait pas, mais cette équation donne un plan pour écrire deux matrices (grilles) et pour les multiplier. Les règles pour multiplier une matrice par une autre sont un peu compliquées, mais voici les deux matrices selon le plan, puis leur produit :
Matrice de p
| États d'électrons | n-a | n-b | n-c | .... | |
| n | p(n←n-a) | p(n←n-b) | p(n←n-c) | ..... | |
| n-a | p(n-a←n-a) | p(n-a←n-b) | p(n-a←n-c) | ..... | |
| n-b | p(n-b←n-a) | p(n-b←n-b) | p(n-b←n-c) | ..... | |
| transition.... | ..... | ..... | ..... | ..... |
Matrice de q
| États d'électrons | n-b | n-c | n-d | .... | |
| n-a | q(n-a←n-b) | q(n-a←n-c) | q(n-a←n-d) | ..... | |
| n-b | q(n-b←n-b) | q(n-b←n-c) | q(n-b←n-d) | ..... | |
| n-c | q(n-c←n-b) | q(n-c←n-c) | q(n-c←n-d) | ..... | |
| transition.... | ..... | ..... | ..... | ..... |
La matrice du produit des deux matrices ci-dessus, telle que spécifiée par l'équation pertinente dans l'article de Heisenberg de 1925, est la suivante
| États d'électrons | n-b | n-c | n-d | ..... |
| n | A | ..... | ..... | ..... |
| n-a | ..... | B | ..... | ..... |
| n-b | ..... | ..... | C | ..... |
Où :
A=p(n←n-a)*q(n-a←n-b)+p(n←n-b)*q(n-b←n-b)+p(n←n-c)*q(n-c←n-b)+.....
B=p(n-a←n-a)*q(n-a←n-c)+p(n-a←n-b)*q(n-b←n-c)+p(n-a←n-c)*q(n-c←n-c)+.....
C=p(n-b←n-a)*q(n-a←n-d)+p(n-b←n-b)*q(n-b←n-d)+p(n-b←n-c)*q(n-d←n-d)+.....
et ainsi de suite.
Si les matrices étaient inversées, les valeurs suivantes en résulteraient :
A=q(n←n-a)*p(n-a←n-b)+q(n←n-b)*p(n-b←n-b)+q(n←n-c)*p(n-c←n-b).....+
B=q(n-a←n-a)*p(n-a←n-c)+q(n-a←n-b)*p(n-b←n-c)+q(n-a←n-c)*p(n-c←n-c).....+
C=q(n-b←n-a)*p(n-a←n-d)+q(n-b←n-b)*p(n-b←n-d)+q(n-b←n-c)*p(n-d←n-d)+.....
et ainsi de suite.
Notez comment le changement de l'ordre de multiplication modifie les nombres, pas à pas, qui sont effectivement multipliés.

Lumière visible émise par l'hydrogène incandescent. (Longueurs d'onde en nanomètres).
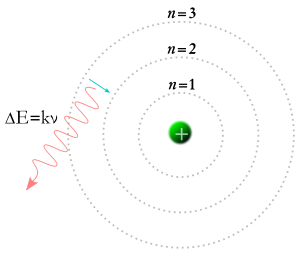
Un électron tombe en orbite basse et un photon est créé.
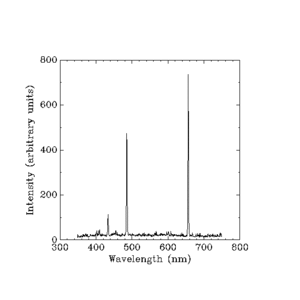
Des intensités espacées dans des unités arbitraires
Au-delà de Heisenberg
Le travail de Werner Heisenberg semble briser un blocage. Très vite, de nombreuses autres façons d'expliquer les choses sont venues de personnes telles que Louis de Broglie, Max Born, Paul Dirac, Wolfgang Pauli et Erwin Schrödinger. Le travail de chacun de ces physiciens est sa propre histoire. Les mathématiques utilisées par Heisenberg et les personnes qui l'ont précédé ne sont pas très difficiles à comprendre, mais les équations sont rapidement devenues très compliquées au fur et à mesure que les physiciens se sont penchés sur le monde atomique.
Autres mystères
Au début de la mécanique quantique, Albert Einstein a suggéré que si c'était le cas, la mécanique quantique signifierait qu'il y aurait une "action effrayante à distance". Il s'est avéré que la mécanique quantique avait raison, et que ce qu'Einstein avait utilisé comme raison pour rejeter la mécanique quantique s'est en fait produit. Ce type de "connexion effrayante" entre certains événements quantiques est maintenant appelé "intrication quantique".
Lorsqu'une expérience réunit deux choses (photons, électrons, etc.), elles doivent alors partager une description commune en mécanique quantique. Lorsqu'elles sont ensuite séparées, elles conservent la même description en mécanique quantique ou "état". Dans le diagramme, une caractéristique (par exemple, le spin "ascendant") est dessinée en rouge, et sa contrepartie (par exemple, le spin "descendant") est dessinée en bleu. La bande violette signifie que lorsque, par exemple, deux électrons sont mis ensemble, la paire partage les deux caractéristiques. Ainsi, les deux électrons peuvent soit faire un spin ascendant, soit un spin descendant. Lorsqu'ils sont ensuite séparés, l'un restant sur Terre et l'autre allant sur une planète de l'étoile Alpha Centauri, ils ont encore chacun les deux spins. En d'autres termes, chacun d'eux peut "décider" de se montrer comme un électron en rotation ascendante ou descendante. Mais si, plus tard, quelqu'un mesure l'autre, il doit "décider" de se montrer comme ayant le spin opposé.
Einstein a fait valoir que sur une si grande distance, il était fou de penser que le fait de forcer un électron à montrer son spin ferait alors en sorte que l'autre électron présente une caractéristique opposée. Il a déclaré que les deux électrons devaient être en rotation vers le haut ou vers le bas depuis le début, mais que la mécanique quantique ne pouvait pas prédire quelle caractéristique chaque électron avait. Le fait de ne pas pouvoir prédire, de ne pouvoir regarder que l'un d'entre eux avec la bonne expérience, signifie que la mécanique quantique ne peut pas expliquer quelque chose d'important. C'est pourquoi, selon Einstein, la mécanique quantique a un grand trou. La mécanique quantique était incomplète.
Plus tard, il s'est avéré que les expériences ont montré que c'était Einstein qui avait tort.
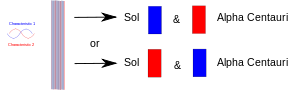
Deux particules enchevêtrées sont séparées : l'une sur la Terre et l'autre emmenée sur une planète lointaine. La mesure de l'une d'entre elles l'oblige à "décider" du rôle qu'elle doit jouer, et l'autre doit ensuite jouer l'autre rôle chaque fois qu'elle est mesurée (après cela).
Le principe d'incertitude de Heisenberg
En 1925, Werner Heisenberg a décrit le principe d'incertitude, selon lequel plus on en sait sur l'endroit où se trouve une particule, moins on peut savoir à quelle vitesse elle va et dans quelle direction. En d'autres termes, plus nous en savons sur la vitesse et la direction d'une petite chose, moins nous pouvons en savoir sur sa position. Les physiciens parlent généralement de l'élan dans ces discussions au lieu de parler de la vitesse. L'élan est simplement la vitesse d'une chose dans une certaine direction multipliée par sa masse.
La raison du principe d'incertitude d'Heisenberg est que nous ne pouvons jamais connaître à la fois l'emplacement et la quantité de mouvement d'une particule. La lumière étant une particule abondante, elle est utilisée pour mesurer d'autres particules. La seule façon de la mesurer est de faire rebondir l'onde lumineuse sur la particule et d'enregistrer les résultats. Si un faisceau lumineux de haute énergie, ou de haute fréquence, est utilisé, nous pouvons dire précisément où il se trouve, mais nous ne pouvons pas dire à quelle vitesse il allait. En effet, le photon à haute énergie transfère de l'énergie à la particule et modifie la vitesse de la particule. Si nous utilisons un photon de faible énergie, nous pouvons dire à quelle vitesse il va, mais pas où il se trouve. C'est parce que nous utilisons une lumière de plus grande longueur d'onde. La longueur d'onde plus longue signifie que la particule peut se trouver n'importe où le long de l'onde.
Le principe dit aussi qu'il y a de nombreuses paires de mesures pour lesquelles nous ne pouvons pas connaître les deux sur une particule (une très petite chose), peu importe nos efforts. Plus nous en apprenons sur l'une de ces paires, moins nous pouvons en savoir sur l'autre.
Même Albert Einstein a eu du mal à accepter un concept aussi bizarre et, dans un débat bien connu, il a déclaré : "Dieu ne joue pas aux dés". À cela, le physicien danois Niels Bohr a répondu de façon célèbre : "Einstein, ne dis pas à Dieu ce qu'il doit faire".
Utilisations de QM
Les électrons entourent le noyau de chaque atome. Des liaisons chimiques relient les atomes pour former des molécules. Une liaison chimique relie deux atomes lorsque des électrons sont partagés entre ces atomes. La MQ est donc la physique de la liaison chimique et de la chimie. La MQ nous aide à comprendre comment les molécules sont fabriquées et quelles sont leurs propriétés.
QM peut également nous aider à comprendre de grandes choses, comme les étoiles et même l'univers tout entier. La MQ est une partie très importante de la théorie de la naissance de l'univers appelée le Big Bang.
Tout ce qui est fait de matière est attiré par une autre matière en raison d'une force fondamentale appelée gravité. La théorie d'Einstein qui explique la gravité est appelée théorie de la relativité générale. Un problème de la physique moderne est que certaines conclusions de la MQ ne semblent pas être en accord avec la théorie de la relativité générale.
La GQ est la partie de la physique qui peut expliquer pourquoi toute technologie électronique fonctionne comme elle le fait. Ainsi, la GQ explique comment les ordinateurs fonctionnent, car les ordinateurs sont des machines électroniques. Mais les concepteurs des premiers matériels informatiques des années 1950 ou 1960 n'avaient pas besoin de penser à la GQ. Les concepteurs de radios et de télévisions de l'époque ne pensaient pas non plus à la gestion de la qualité. Cependant, la conception des circuits intégrés et des technologies de mémoire informatique les plus puissants de ces dernières années nécessite une gestion de la qualité.
QM a également rendu possible des technologies telles que :
- Spectroscopie
- Lasers
- IRM
- CD et DVD
Pourquoi la GQ est difficile à apprendre
La GQ est un sujet difficile pour plusieurs raisons :
- QM explique les choses de manière très différente de ce que nous apprenons sur le monde quand nous sommes enfants.
- La compréhension de la MQ nécessite plus de mathématiques que l'algèbre et le simple calcul. Elle exige également de l'algèbre matricielle, des nombres complexes, la théorie des probabilités et des équations différentielles partielles.
- Les physiciens ne sont pas sûrs de ce que certaines des équations de la MQ nous apprennent sur le monde réel.
- QM suggère que les atomes et les particules subatomiques se comportent de manière étrange, complètement différente de tout ce que nous voyons dans notre vie quotidienne.
- QM décrit des choses qui sont extrêmement petites, donc nous ne pouvons pas en voir certaines sans équipement spécial, et nous ne pouvons pas en voir beaucoup du tout.
QM décrit la nature d'une manière différente de celle que nous avons l'habitude d'utiliser pour la science. Elle nous indique la probabilité que certaines choses se produisent, plutôt que de nous dire qu'elles vont certainement se produire.
Un exemple est l'expérience à double fente de Young. Si nous tirons des photons simples (unités de lumière simples) à partir d'un laser sur une feuille de film photographique, nous verrons un seul point de lumière sur le film développé. Si nous plaçons une feuille de métal entre les deux, et que nous faisons deux fentes très étroites dans la feuille, lorsque nous tirons de nombreux photons sur la feuille de métal, et qu'ils doivent passer à travers les fentes, alors nous verrons quelque chose de remarquable. Tout au long de la feuille de film développée, nous verrons une série de bandes claires et sombres. Nous pouvons utiliser les mathématiques pour savoir exactement où se trouveront les bandes claires et quelle était la luminosité qui les a créées, c'est-à-dire que nous pouvons dire à l'avance combien de photons tomberont sur chaque bande. Mais si nous ralentissons le processus et que nous voyons où chaque photon se pose sur l'écran, nous ne pouvons jamais dire à l'avance où le prochain apparaîtra. Nous pouvons savoir avec certitude qu'il est très probable qu'un photon frappe la bande lumineuse centrale, et qu'il est de moins en moins probable qu'un photon apparaisse sur des bandes de plus en plus éloignées du centre. Nous savons donc avec certitude que les bandes seront les plus brillantes au centre et qu'elles s'atténueront de plus en plus loin. Mais on ne sait jamais avec certitude quel photon ira dans quelle bande.
L'une des conclusions étranges de la théorie de la MQ est l'effet "chat de Schrödinger". Certaines propriétés d'une particule, telles que sa position, sa vitesse de déplacement, sa direction et son "spin", ne peuvent être évoquées tant que quelque chose ne les mesure pas (un photon rebondissant sur un électron compterait comme une mesure de sa position, par exemple). Avant la mesure, la particule est dans une "superposition d'états", dans laquelle ses propriétés ont plusieurs valeurs en même temps. Selon Schrödinger, la mécanique quantique semble dire que si quelque chose (comme la vie ou la mort d'un chat) est déterminé par un événement quantique, alors son état sera déterminé par l'état qui résulte de l'événement quantique, mais seulement au moment où quelqu'un regarde l'état de l'événement quantique. Dans la période précédant l'examen de l'état de l'événement quantique, peut-être que "le chat vivant et le chat mort (pardonnez l'expression) sont mélangés ou étalés à parts égales".
Réduit la constante de Planck
Les gens utilisent souvent le symbole ℏ {\displaystyle \hbar }

Exemple
La particule dans un puits unidimensionnel est l'exemple le plus simple montrant que l'énergie d'une particule ne peut avoir que des valeurs spécifiques. On dit que l'énergie est "quantifiée". Le puits a une énergie potentielle nulle à l'intérieur d'une plage et une énergie potentielle infinie partout en dehors de cette plage. Pour le cas à une dimension dans la
- ℏ 2 2 m d 2 ψ d x 2 = E ψ . {\disdisplaystyle -{\frac {bar ^{2}}{2m}}{\frac {d^{2}\psi }{dx^{2}}}=E\psi . }
En utilisant des équations différentielles, nous pouvons voir que ψ
ψ = A e i k x + B e - i k x E = ℏ 2 k 2 2 m {\displaystyle \psi =Ae^{ikx}+Be^{-ikx}\;\;\;\;\;\;\;E={\frac {\hbar ^{2}k^{2}}{2m}}}
ou
ψ = C sin k x + D cos k x {\displaystyle \psi =C\sin kx+D\cos kx\ ; }
Les parois de la boîte signifient que la fonction d'onde doit avoir une forme spéciale. La fonction d'onde de la particule doit être nulle chaque fois que les parois sont infiniment hautes. À chaque paroi :
ψ = 0 a t x = 0 , x = L {\displaystyle \psi =0\;\mathrm {at} \;\;x=0,\;x=L}
Considérons que x = 0
- sin 0 = 0, cos 0 = 1. Pour satisfaire ψ = 0 {\displaystyle \scriptstyle \psi =0\ ; }
le terme cos doit être supprimé. D'où D = 0
Maintenant, réfléchissez : ψ = C sin k x {\displaystyle \scriptstyle \psi =C\sin kx\ ; }
- at x = L, ψ = C sin k L = 0 {\displaystyle \scriptstyle \psi =C\sin kL=0\ ; }
- Si C = 0, alors ψ = 0 {\displaystyle \scriptstyle \psi =0\ ; }
pour tous les x. Cette solution n'est pas utile.
- Par conséquent, sin kL = 0 doit être vrai, ce qui nous donne
k L = n π n = 1 , 2 , 3 , 4 , 5 , ... kL=n\pi \;\;\;\;n=1,2,3,4,5,...\ ; }
On peut voir que n
Pages connexes
- Onde électromagnétique
- Electron
- Photon
- L'intrication quantique
- Équation de Schrödinger
Questions et réponses
Q : Qu'est-ce que la mécanique quantique ?
R : La mécanique quantique est une branche de la physique qui explique le fonctionnement de l'univers à une échelle plus petite que celle des atomes. Elle est également connue sous le nom de physique quantique ou de théorie quantique.
Q : Que signifie le terme "quantique" ?
R : Le terme "quantum" vient du latin et signifie "combien". Un quantum d'énergie est la plus petite quantité possible (ou la plus petite quantité supplémentaire), et la mécanique quantique décrit comment cette énergie se déplace ou interagit.
Q : Que sont les particules subatomiques ?
R : Les particules subatomiques sont des particules qui composent les atomes, comme les protons, les neutrons et les électrons. Elles sont encore plus petites que les atomes.
Q : Comment la mécanique quantique décrit-elle le fonctionnement de ces particules ?
R : La mécanique quantique fournit des règles mathématiques pour étudier les particules subatomiques et les ondes électromagnétiques afin de comprendre leur comportement et leurs interactions les unes avec les autres.
Q : Qu'est-ce que la dualité onde-particule ?
R : La dualité onde-particule fait référence au fait que les particules et les ondes peuvent se comporter l'une comme l'autre - ce ne sont pas deux entités distinctes, mais plutôt quelque chose comme les deux combinées en un seul phénomène.
Q : Comment peut-on décrire la physique moderne à l'aide de la mécanique quantique ?
R : La physique et la chimie modernes peuvent être expliquées en leur appliquant les règles mathématiques de la mécanique quantique.
Rechercher dans l'encyclopédie







