Constante de Planck

Contexte

Symboles utilisés dans cet article.
Symbole Signification E Énergie h Constante de Planck k La constante de Boltzmann c la vitesse de la lumière λ longueur d'onde du rayonnement ν fréquence de rayonnement T température absolue

Entre 1670 et 1900, les scientifiques se sont penchés sur la nature de la lumière. Certains scientifiques pensaient que la lumière était constituée de plusieurs millions de minuscules particules. D'autres scientifiques pensaient que la lumière était une onde.

La lumière : ondes ou particules ?

En 1678, Christiaan Huygens a écrit le livre Traité de la lumière. Il croyait que la lumière était composée d'ondes. Il disait que la lumière ne pouvait pas être composée de particules car la lumière de deux faisceaux ne rebondit pas l'un sur l'autre. En 1672, Isaac Newton a écrit le livre Opticks. Il croyait que la lumière était composée de particules rouges, jaunes et bleues qu'il appelait corpuscules. Newton a expliqué cela par son "expérience des deux prismes". Le premier prisme a décomposé la lumière en différentes couleurs. Le second prisme a fusionné ces couleurs pour donner une lumière blanche.

Au XVIIIe siècle, c'est la théorie de Newton qui a reçu le plus d'attention. En 1803, Thomas Young a décrit l'"expérience de la double fente". Dans cette expérience, la lumière passant à travers deux fentes étroites se perturbe elle-même. Il en résulte un motif qui montre que la lumière est composée d'ondes. Pendant le reste du XIXe siècle, c'est la théorie des ondes de la lumière qui a retenu le plus l'attention. Dans les années 1860, James Clerk Maxwell a développé des équations qui décrivent les radiations électromagnétiques comme des ondes.

La théorie du rayonnement électromagnétique traite la lumière, les ondes radio, les micro-ondes et de nombreux autres types d'ondes comme une seule et même chose, sauf qu'elles ont des longueurs d'onde différentes. La longueur d'onde de la lumière que nous pouvons voir avec nos yeux se situe approximativement entre 400 et 600 nm. La longueur d'onde des ondes radio varie de 10 m à 1500 m et celle des micro-ondes est d'environ 2 cm. Dans le vide, toutes les ondes électromagnétiques se déplacent à la vitesse de la lumière. La fréquence de l'onde électromagnétique est donnée par :

ν = c λ {\displaystyle \nu ={\frac {c}{\lambda }}} .

Les symboles sont définis ici.

Radiateurs à corps noir

Toutes les choses chaudes émettent un rayonnement thermique, qui est un rayonnement électromagnétique. Pour la plupart des choses sur Terre, ces radiations se situent dans la gamme des infrarouges, mais quelque chose de très chaud (1000 °C ou plus), émet des radiations visibles, c'est-à-dire de la lumière. À la fin du XIXe siècle, de nombreux scientifiques ont étudié les longueurs d'onde du rayonnement électromagnétique des radiateurs à corps noir à différentes températures.

Loi Rayleigh-Jeans

Lord Rayleigh a publié pour la première fois les bases de la loi Rayleigh-Jeans en 1900. La théorie était basée sur la théorie cinétique des gaz. Sir James Jeans a publié une théorie plus complète en 1905. Cette loi concerne la quantité et la longueur d'onde de l'énergie électromagnétique émise par un radiateur à corps noir à différentes températures. L'équation qui la décrit est la suivante :

B λ ( T ) = 2 c k T λ 4 {\displaystyle B_{\lambda }(T)={\frac {2ckT}{\lambda ^{4}}} .

Pour les rayonnements de grande longueur d'onde, les résultats prévus par cette équation correspondaient bien aux résultats pratiques obtenus en laboratoire. Cependant, pour les courtes longueurs d'onde (lumière ultraviolette), la différence entre la théorie et la pratique était si importante qu'elle a valu le surnom de "catastrophe ultraviolette".

La loi de Planck

En 1895, Wien a publié les résultats de ses études sur les radiations d'un corps noir. Sa formule était la suivante :

B λ ( T ) = 2 h c 2 λ 5 e - h c λ k T {\displaystyle B_{\lambda }(T)={\frac {2hc^{2}}{\lambda ^{5}}}e^{-{\frac {hc}{\lambda kT}}}} .

Cette formule a bien fonctionné pour les rayonnements électromagnétiques de courte longueur d'onde, mais n'a pas donné de bons résultats avec les grandes longueurs d'onde.

En 1900, Max Planck publie les résultats de ses études. Il a essayé de développer une expression pour le rayonnement du corps noir exprimée en termes de longueur d'onde en supposant que le rayonnement consistait en de petits quanta, puis de voir ce qui se passait si les quanta étaient rendus infiniment petits. (Il s'agit d'une approche mathématique standard). L'expression était :

B λ ( T ) = 2 h c 2 λ 5 1 e h c λ k T - 1 {\displaystyle B_{\lambda }(T)={\frac {2hc^{2}}{\lambda ^{5}}~{\frac {1}{e^{\frac {hc}{\lambda kT}}}-1}}} .

Si l'on laisse la longueur d'onde de la lumière devenir très importante, on peut alors montrer que les relations Raleigh-Jeans et Planck sont presque identiques.

Il a calculé h et k et a constaté que

h = 6,55×10-27 erg-sec.

k = 1,34×10-16 erg-deg-1.

Ces valeurs sont proches des valeurs acceptées de nos jours, qui sont respectivement de 6,62606×10-34 et de 1,38065×10-16. La loi Planck est en accord avec les données expérimentales, mais sa pleine signification n'a été appréciée que plusieurs années plus tard.

La théorie quantique de la lumière

Il s'avère que les électrons sont délogés par l'effet photoélectrique si la lumière atteint une fréquence seuil. En dessous de ce seuil, aucun électron ne peut être émis par le métal. En 1905, Albert Einstein a publié un article expliquant cet effet. Einstein proposait qu'un faisceau de lumière n'est pas une onde se propageant dans l'espace, mais plutôt une collection de paquets d'ondes discrètes (photons), chacun avec de l'énergie. Einstein a déclaré que l'effet était dû au fait qu'un photon frappait un électron. Cela a démontré la nature particulaire de la lumière.

Einstein a également découvert que les rayonnements électromagnétiques de grande longueur d'onde n'avaient aucun effet. Einstein a déclaré que cela était dû au fait que les "particules" n'avaient pas assez d'énergie pour perturber les électrons.

Plank a suggéré que l'énergie de chaque photon était liée à la fréquence du photon par la constante de Planck. Cela pourrait s'écrire mathématiquement comme suit :

E = h ν = h c λ {\displaystyle E=h\nu ={\frac {hc}{\lambda }}} .

Plank a reçu le prix Nobel en 1918 en reconnaissance des services qu'il a rendus à l'avancement de la physique par sa découverte des quanta d'énergie. En 1921, Einstein a reçu le prix Nobel pour avoir relié la constante de Planck à l'effet photoélectrique.

Illustration tirée de la lettre originale de Newton à la Royal Society (1er janvier 1671 [calendrier julien]). Le S représente la lumière du soleil. La lumière entre les plans BC et DE est en couleur. Ces couleurs sont recombinées pour former la lumière du soleil sur le plan GH


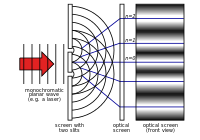
L'expérience de Young sur la double fente


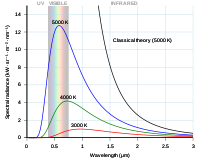
Courbe de Rayleigh-Jeans et courbe de Planck tracées en fonction de la longueur d'onde du photon.


Conférence Solway 1911. Planck, Einstein et Jeans sont debout. Planck est le deuxième en partant de la gauche. Einstein est le deuxième à partir de la droite. Jeans est cinquième à partir de la droite. Wien est assis, troisième à partir de la droite

Candidature

La constante de Planck est importante dans de nombreuses applications. Quelques-unes sont énumérées ci-dessous.

Modèle de l'atome de Bohr

En 1913, Niels Bohr a publié le modèle Bohr de la structure d'un atome. Selon Bohr, le moment angulaire des électrons qui tournent autour du noyau ne peut avoir que certaines valeurs. Ces valeurs sont données par l'équation

L = n h 2 π {\displaystyle L=n{\frac {h}{2\pi }}}

où

L = moment angulaire associé à un niveau.

n = nombre entier positif.

h = constante de Planck.

Le modèle de l'atome de Bohr peut être utilisé pour calculer l'énergie des électrons à chaque niveau. Les électrons remplissent normalement les états les moins nombreux d'un atome. Si l'atome reçoit de l'énergie d'un courant électrique, par exemple, les électrons seront excités dans un état supérieur. Les électrons retomberont alors dans un état inférieur et perdront leur énergie supplémentaire en émettant un photon. Comme les niveaux d'énergie ont des valeurs spécifiques, les photons auront des niveaux d'énergie spécifiques. La lumière émise de cette manière peut être divisée en différentes couleurs à l'aide d'un prisme. Chaque élément a son propre motif. Le motif du néon est illustré ci-contre.

Le principe d'incertitude de Heisenberg

En 1927, Werner Heisenberg a publié le principe d'incertitude. Ce principe stipule qu'il n'est pas possible d'effectuer une mesure sans perturber la chose mesurée. Il fixe également une limite à la perturbation minimale causée par une mesure.

Dans le monde macroscopique, ces perturbations font très peu de différence. Par exemple, si l'on mesure la température d'un flacon de liquide, le thermomètre absorbera une petite quantité d'énergie lorsqu'il se réchauffera. Cela entraînera une petite erreur dans la lecture finale, mais cette erreur est minime et sans importance.

En mécanique quantique, les choses sont différentes. Certaines mesures sont faites en regardant le modèle des photons diffusés. La diffusion Compton en est un exemple. Si la position et l'impulsion d'une particule sont mesurées, le principe d'incertitude stipule qu'il y a un compromis entre la précision avec laquelle l'impulsion est mesurée et la précision avec laquelle la position est mesurée. L'équation qui décrit ce compromis est la suivante :

Δ x Δ p ≳ h {\displaystyle \Delta x\,\Delta p\gtrsim h\qquad \qquad \qquad }

où

Δp = incertitude dans l'élan.

Δx = incertitude dans la position.

h = constante de Planck.

Couleur des diodes électroluminescentes

Dans le circuit électrique illustré à droite, la chute de tension aux bornes de la diode électroluminescente (DEL) dépend du matériau de la DEL. Pour les diodes au silicium, la chute est de 0,6 V. Cependant, pour les LED, elle se situe entre 1,8 V et 2,7 V. Cette information permet à l'utilisateur de calculer la constante de Planck.

L'énergie nécessaire à un électron pour franchir la barrière de potentiel dans le matériau LED est donnée par

E = Q e V L {\displaystyle E=Q_{e}V_{L}\,}

où

Qe est la charge d'un électron.

VL est la chute de tension aux bornes de la LED.

Lorsque l'électron se désintègre à nouveau, il émet un photon de lumière. L'énergie du photon est donnée par la même équation que celle utilisée dans l'effet photoélectrique. Si ces équations sont combinées, la longueur d'onde de la lumière et la tension sont liées par

λ = h c V L Q e {\displaystyle \lambda ={\frac {hc}{V_{L}Q_{e}}}\,}

Le tableau ci-dessous peut être calculé à partir de cette relation.

Couleur	Longueur d'onde  (nm)	Tension
feu rouge	650	1.89
feu vert	550	2.25
lumière bleue	470	2.62

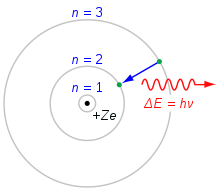
Le modèle de l'atome de Bohr. Un électron qui tombe de la coquille n=3 à la coquille n=2 perd de l'énergie. Cette énergie est emportée sous la forme d'un photon unique.


Spectre visible du néon. Chaque ligne représente une paire différente de niveaux d'énergie.


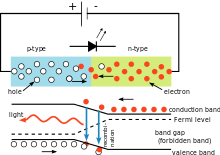
Simple circuit de LED qui illustre l'utilisation de la constante de Planck. La couleur de la lumière émise dépend de la chute de tension aux bornes de la diode. La longueur d'onde de la lumière peut être calculée à l'aide de la constante de Planck.

Valeur de la constante de Planck et redéfinition du kilogramme

Depuis sa découverte, les mesures de h sont devenues bien meilleures. Planck a d'abord indiqué que la valeur de h était de 6,55×10-27 erg-sec. Cette valeur se situe à moins de 5 % de la valeur actuelle.

Au 3 mars 2014, la meilleure mesure de h en unités SI est de 6,62606957×10-34 J-s. Le chiffre équivalent en unités cgs est 6,62606957×10-27 erg-sec. L'incertitude relative de h est de 4,4×10-8.

La constante de Planck réduite (ħ) est une valeur qui est parfois utilisée en mécanique quantique. Elle est définie par

ℏ = h 2 π {\displaystyle \hbar ={\frac {h}{2\pi }}} .

Les unités de Planck sont parfois utilisées en mécanique quantique au lieu du SI. Dans ce système, la constante de Planck réduite a une valeur de 1, la valeur de la constante de Planck est donc 2π.

La constante de Plancks peut maintenant être mesurée avec une très grande précision. Cela a amené le BIPM à envisager une nouvelle définition du kilogramme. Le prototype international du kilogramme n'est plus utilisé pour définir le kilogramme. Au lieu de cela, le BIPM définit la constante de Planck pour avoir une valeur exacte. Les scientifiques utilisent cette valeur et les définitions du mètre et de la seconde pour définir le kilogramme.

 

Valeur de la constante de Planck théorique

La constante de Planck peut également être dérivée mathématiquement :

 

h = μ 0 π 12 c 3 [ q 0 [ 0,9163 a 0 ] 2 ] 2 f 1 r 5 ⋅ s = 6,63 × 10 - 34 J ⋅ s {\displaystyle h={\frac {\mu _{0}\pi }{12c^{3}}}{[{q_{0}}{[0.9163a_{0}]}^{2}]^{2}}{f_{1r}}^{5}\cdot {s}=6,63\fois 10^{-34}J\cdot s}

Ici, μ 0 {\displaystyle \mu _{0}} est la perméabilité de l'espace libre, c {\displaystyle c} est la vitesse de la lumière, q 0 {\displaystyle q_{0}} est la charge électrique de l'électron, a 0 {\displaystyle a_{0}} est le rayon de Bohr, et f 1 r {\displaystyle f_{1r}} est la fréquence de révolution de l'électron dans un atome d'hydrogène ( f 1 r = 3.29 × 10 15 r e v / s ) {\displaystyle (f_{1r}=3.29\times 10^{15}rev/s)} . Lorsque ces valeurs constantes sont substituées à la constante de Planck théorique, la valeur de la constante de Planck théorique est exactement égale à la valeur expérimentale.

Pages connexes

• La dualité onde-particule