Pi

Approximation

Pi s'écrit souvent de manière formelle comme π ou la lettre grecque π comme raccourci. Pi est également un nombre irrationnel, ce qui signifie qu'il ne peut pas être écrit sous forme de fraction ( a b / a sur b), où "a" et "b" sont des nombres entiers. Cela signifie essentiellement que les chiffres de Pi qui se trouvent à droite de la décimale sont éternels sans se répéter, et qu'il est impossible d'écrire la valeur exacte de Pi sous forme de nombre. Pi peut seulement être approximé, ou mesuré à une valeur qui est assez proche pour des raisons pratiques.

Une valeur proche de pi est 3,141592653589793238462643... Une approximation de la fraction commune de pi est 22 7 {\displaystyle 22 \over 7} ce qui donne environ 3,14285714. Cette approximation est éloignée de 0,04 % de la valeur réelle de pi. Bien que cette approximation soit acceptée pour la plupart de son utilisation dans la vie réelle, la fraction 355 113 est plus précise (donnant environ 3,14159292), et peut être utilisée lorsqu'une valeur plus proche de pi est nécessaire. Les ordinateurs peuvent être utilisés pour obtenir de meilleures approximations de pi.

En mars 2019, Emma Haruka Iwao a calculé la valeur de pi à 31,4 trillions de chiffres.

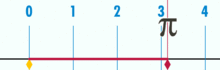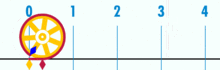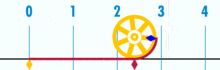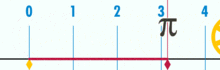
Un diagramme montrant comment trouver π en utilisant un cercle d'un diamètre de un. La circonférence de ce cercle est π.

Histoire

La valeur de pi était connue des mathématiciens de l'Inde ancienne comme Bhaskaracharya et Aryabhatta.

Les mathématiciens connaissent le pi depuis des milliers d'années parce qu'ils travaillent avec des cercles depuis le même temps. Des civilisations aussi anciennes que celle des Babyloniens ont été capables d'approximer pi à de nombreux chiffres, comme la fraction 25/8 et 256/81. La plupart des historiens pensent que les anciens Égyptiens n'avaient aucune idée de π et que la correspondance est une coïncidence.

La première référence écrite à pi date de 1900 avant J.-C. Vers 1650 avant J.-C., l'Égyptien Ahmès a donné une valeur au papyrus du Rhin. Les Babyloniens ont pu constater que la valeur de pi était légèrement supérieure à 3 en faisant simplement un grand cercle puis en collant un morceau de corde sur la circonférence et le diamètre, en prenant note de leurs distances, puis en divisant la circonférence par le diamètre.

La connaissance du nombre pi est retournée en Europe et entre les mains des Hébreux, qui ont rendu ce nombre important dans une section de la Bible appelée Ancien Testament. Après cela, la façon la plus courante d'essayer de trouver pi était de dessiner une forme à plusieurs côtés à l'intérieur de n'importe quel cercle et d'utiliser la surface de la forme pour trouver pi. Le philosophe grec Archimède, par exemple, a utilisé une forme de polygone à 96 côtés pour trouver la valeur de pi, mais les Chinois en 500 de notre ère ont pu utiliser un polygone à 16 384 côtés pour trouver la valeur de pi. Les Grecs, comme Anaxagore de Clazomène, étaient également occupés à découvrir d'autres propriétés du cercle, comme la façon de faire des carrés de cercles et de quadriller le nombre pi. Depuis lors, de nombreuses personnes ont essayé de découvrir des valeurs de plus en plus exactes de pi.

Une histoire de pi
Philosophe	Date	Approximation
Claudius Ptolemy	environ 150 CE	3.1416
Zu Chongzhi	430-501 CE	3.1415929203
al-Khwarizmi	environ 800 CE	3.1416
al-Kashi	vers 1430	3.14159265358979
Viète	1540–1603	3.141592654
Roomen	1561–1615	3.14159265358979323
Van Ceulen	vers 1600	3.14159265358979323846264338327950288

Au XVIe siècle, des moyens de plus en plus efficaces pour trouver pi sont apparus, comme la formule compliquée mise au point par l'avocat français François Viète. La première utilisation du symbole grec "π" a été faite dans un essai écrit en 1706 par William Jones.

Un mathématicien du nom de Lambert a également montré en 1761 que le nombre pi était irrationnel, c'est-à-dire qu'il ne peut pas être écrit sous forme de fraction selon les normes normales. Un autre mathématicien du nom de Lindeman a également pu montrer en 1882 que pi faisait partie du groupe de nombres connus sous le nom de transcendantaux, qui sont des nombres qui ne peuvent pas être la solution d'une équation polynomiale.

Pi peut également être utilisé pour découvrir bien d'autres choses que des cercles. Les propriétés de Pi lui ont permis d'être utilisé dans bien d'autres domaines des mathématiques que la géométrie, qui étudie les formes. Certains de ces domaines sont l'analyse complexe, la trigonométrie et les séries.

Pi dans la vie réelle

Aujourd'hui, il existe différentes façons de calculer de nombreux chiffres de π. Cette méthode est cependant d'une utilité limitée.

Pi peut parfois être utilisé pour calculer la surface ou la circonférence de n'importe quel cercle. Pour trouver la circonférence d'un cercle, utilisez la formule C (circonférence) = π fois le diamètre. Pour trouver l'aire d'un cercle, utilisez la formule π (rayon²). Cette formule s'écrit parfois A = π r 2 {\displaystyle A=\pi r^{2}} où r est la variable pour le rayon d'un cercle quelconque et A est la variable pour l'aire de ce cercle.

Pour calculer la circonférence d'un cercle avec une erreur de 1 mm :

• 4 chiffres sont nécessaires pour un rayon de 30 mètres
• 10 chiffres pour un rayon égal à celui de la terre
• 15 chiffres pour un rayon égal à la distance entre la terre et le soleil.

Les gens célèbrent généralement le 14 mars comme le jour Pi car le 14 mars s'écrit aussi 3/14, ce qui représente les trois premiers nombres 3,14 dans l'approximation de pi. Le jour Pi a commencé en 2001.

Pages connexes

• Cercle