Machine abstraite
Un automate (un automate, plusieurs automates) est un concept issu des mathématiques. Ce concept est parfois appelé machine à états. C'est comme une machine abstraite.
Une telle machine peut être saisie, qui est soit rejetée, soit acceptée. C'est comme un distributeur automatique. Lorsque l'on achète quelque chose, il faut insérer des pièces (ou de l'argent) dans la machine. Si ce sont les bonnes pièces, elles sont acceptées, et l'article demandé est déposé pour pouvoir être retiré. Si les pièces sont fausses, elles sont rejetées.
En interne, l'automate a différents états dans lesquels il peut se trouver. L'alimentation de son entrée peut (ou non) changer son état. De cette façon, l'automate parcourt toutes les entrées, consommant un élément (que les mathématiciens appellent un symbole) à la fois. Lorsqu'il ne reste plus de symbole, l'automate se trouve dans un certain état. Il peut s'agir d'un état final. Dans ce cas, l'entrée est acceptée. Dans le cas contraire, l'entrée est rejetée.
Si la machine possède un nombre fini d'états dénombrables, on parle de machine à états finis. Un diagramme qui montre tous les états, et les transitions d'une telle machine est appelé diagramme à états finis.
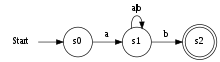
Une représentation commune d'un automate en informatique. Cet automate "accepte" toutes les séquences des lettres a et b qui commencent par un a et se terminent par un b.
Problèmes
Comme dans la vie réelle, il existe des machines trop complexes pour être comprises. Le mathématicien et l'informaticien se demandent donc si un certain automate est minimal. S'il n'est pas minimal, il doit y avoir un autre automate avec moins d'états qui peut faire la même chose. Un exemple d'automate est la machine de Turing.
Questions et réponses
K: Mikä on automaatti?
V: Automaatti on matematiikan käsite, joka on kuin abstrakti kone ja jolle voidaan antaa syötettä, joka joko hylätään tai hyväksytään.
K: Mikä on toinen termi automaatille?
V: Joskus käsitettä kutsutaan tilakoneeksi.
K: Voitko verrata automaattia automaattiin?
V: Kyllä, se on kuin myyntiautomaatti, jossa automaattiin on syötettävä kolikoita tai rahaa, ja jos kolikot ovat oikeita, pyydetty esine pudotetaan, jotta se voidaan ottaa pois.
K: Mitä tapahtuu, kun automaatille annetaan syötettä?
V: Automaatti käy läpi kaikki syötteet, kuluttaa yhden esineen kerrallaan, ja sillä on sisäisesti erilaisia tiloja, joissa se voi olla. Syöttö voi muuttaa tai olla muuttamatta sen tilaa.
K: Mitä tapahtuu, kun automaatilla ei ole enää yhtään symbolia jäljellä?
V: Kun symboleja ei ole jäljellä, automaatti on tietyssä tilassa, joka voi olla lopputila. Jos näin on, syöte hyväksytään, muuten syöte hylätään.
K: Mikä on äärellinen tilakone?
V: Jos automaatilla on laskettavissa oleva äärellinen määrä tiloja, sitä kutsutaan äärelliseksi tila-automaatiksi.
K: Mikä on äärellinen tilakaavio?
V: Kaaviota, joka esittää tällaisen koneen kaikki tilat ja siirtymät, kutsutaan äärelliseksi tilakaavioksi.
Rechercher dans l'encyclopédie