Espace de Minkowski
Dans la relativité spéciale, l'espace-temps de Minkowski est un multiple quadridimensionnel, créé par Hermann Minkowski. Elle comporte quatre dimensions : trois dimensions de l'espace (x, y, z) et une dimension du temps. L'espace-temps de Minkowski a une signature métrique de (-+++), et décrit une surface plane lorsqu'aucune masse n'est présente. Dans cet article, la convention est d'appeler l'espace-temps de Minkowski simplement espace-temps.
Cependant, l'espace-temps de Minkowski ne s'applique que dans le cadre d'une relativité spéciale. La relativité générale utilise la notion d'espace-temps courbe pour décrire les effets de la gravité et du mouvement accéléré.
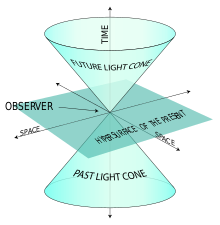
Exemple d'un cône lumineux.
Définition(s)
Mathématiques
L'espace-temps peut être considéré comme un système de coordonnées quadridimensionnel dans lequel les axes sont donnés par
( c t , x , y , z ) [style d'affichage (ct,x,y,z)}
Ils peuvent également être désignés par
( x 1 , x 2 , x 3 , x 4 )
Où x 1 {\displaystyle x_{1}}

d s 2 = - c 2 d t 2 + d x 2 + d y 2 + d z 2 {\displaystyle ds^{2}=-c^{2}dt^{2}+dx^{2}+dy^{2}+dz^{2}}
Cela implique que l'espace-temps a un tenseur métrique donné par
g u v = [ - 1 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 1 ] {\displaystyle g_{uv}={\begin{bmatrix}-1&0&0&0\\0&1&0&0\0&0&1&0\0&0&0&0&0&1\end{bmatrix}}}}
Comme nous l'avons déjà dit, l'espace-temps est partout plat ; dans une certaine mesure, on peut le considérer comme un avion.
Simple
L'espace-temps peut être considéré comme l'"arène" dans laquelle se déroulent tous les événements de l'univers. Tout ce dont on a besoin pour spécifier un point dans l'espace-temps est un certain temps et une orientation spatiale typique. Il est difficile (pratiquement impossible) de visualiser les quatre dimensions, mais on peut faire une certaine analogie, en utilisant la méthode ci-dessous.
Diagrammes espace-temps
Hermann Minkowski a introduit une certaine méthode pour représenter graphiquement les systèmes de coordonnées dans l'espace-temps de Minkowski. Comme on peut le voir à droite, différents systèmes de coordonnées sont en désaccord sur l'orientation spatiale et/ou la position dans le temps d'un objet. Comme vous pouvez le voir sur le diagramme, il n'y a qu'un seul axe spatial (l'axe x) et un seul axe temporel (l'axe ct). Si nécessaire, on peut introduire une dimension spatiale supplémentaire, (l'axe des y) ; malheureusement, c'est la limite du nombre de dimensions : il est impossible de faire un graphique en quatre dimensions. La règle de la représentation graphique dans l'espace-temps de Minkowski est la suivante :
1) L'angle entre l'axe des x et l'axe des x' est donné par t a n ( α ) = v c {\displaystyle tan(\alpha )={\frac {v}{c}}}
2) La vitesse de la lumière dans l'espace-temps fait toujours un angle de 45 degrés avec l'un ou l'autre axe.
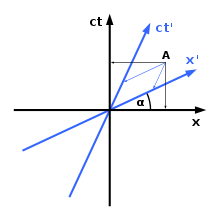
Dans la théorie de la relativité, les deux observateurs attribuent l'événement à A à des moments différents.
L'espace-temps dans la relativité générale
Dans la théorie générale de la relativité, Einstein a utilisé l'équation
R u v - 1 2 g u v R = 8 π T u v {\displaystyle R_{uv}-{\frac {1}{2}}g_{uv}R=8\pi T_{uv}}
Pour permettre à l'espace-temps de se courber réellement ; les effets qui en résultent sont ceux de la gravité.
Pages connexes
- Spacetime
- Relativité spéciale
- Relativité générale
| Contrôle de l'autorité |
|
Questions et réponses
Q : Qu'est-ce que l'espace-temps de Minkowski ?
R : L'espace-temps de Minkowski est un collecteur à quatre dimensions créé par Hermann Minkowski. Il possède trois dimensions d'espace (x, y, z) et une dimension de temps.
Q : Quelle est la signature métrique de l'espace-temps de Minkowski ?
R : La signature métrique de l'espace-temps de Minkowski est (-+++).
Q : Comment l'espace-temps de Minkowski décrit-il une surface plane ?
R : Lorsqu'il n'y a pas de masse, l'espace-temps de Minkowski décrit une surface plane.
Q : L'espace-temps de Minkowski s'applique-t-il à la relativité générale ?
R : Non, l'espace-temps de Minkowski ne s'applique qu'en relativité restreinte. La relativité générale utilise la notion d'espace-temps courbé pour décrire les effets de la gravité et du mouvement accéléré.
Q : Combien de dimensions possède l'Espace-temps de Minkowsi ?
R : L'espace-temps Minkowsi a quatre dimensions - trois dimensions d'espace (x, y, z) et une dimension de temps.
Q : Qui a créé le concept d'espace-temps Minkowsi ?
R : Hermann Minkowksi a créé le concept de l'Espace-temps de MInkowski.
Rechercher dans l'encyclopédie




