Mécanique matricielle
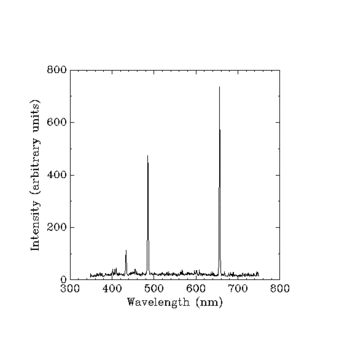
La mécanique des matrices est le premier moyen que les physiciens ont trouvé pour exprimer la physique quantique sous forme mathématique. Werner Heisenberg a d'abord développé cette forme d'expression des lois de la physique comme une équation qu'il pouvait utiliser pour prédire les intensités des photons dans les différentes bandes du spectre de l'hydrogène.

Le professeur et collègue de Heisenberg, Max Born, a vu que son équation était essentiellement le plan de création et de multiplication des matrices. La forme matricielle de la physique quantique est toujours utilisée car elle est utile et pratique pour certains objectifs. D'autres méthodes mathématiques, notamment l'équation d'Erwin Schrödinger utilisant une fonction d'onde, sont mathématiquement équivalentes mais sont plus faciles à utiliser à d'autres fins.
L'un des premiers succès de cette théorie a été annoncé peu après et est maintenant appelé le principe d'incertitude de Heisenberg.
Questions et réponses
Q : Qu'est-ce que la mécanique matricielle ?
R : La mécanique matricielle est une forme d'expression des lois de la physique développée par Werner Heisenberg qui utilise des matrices pour prédire les intensités des photons dans différentes bandes du spectre de l'hydrogène.
Q : Qui a développé la mécanique matricielle ?
R : Werner Heisenberg a initialement développé la mécanique matricielle comme une équation permettant de prédire les intensités des photons dans différentes bandes du spectre de l'hydrogène.
Q : Comment a-t-il été découvert ?
R : Max Born a vu que l'équation d'Heisenberg était essentiellement un schéma pour créer et multiplier des matrices, ce qui a conduit à la découverte de la mécanique matricielle.
Q : Est-il encore utilisé aujourd'hui ?
R : Oui, la mécanique matricielle est encore utilisée aujourd'hui car elle est utile et pratique à certaines fins.
Q : Existe-t-il d'autres moyens mathématiques d'exprimer la physique quantique ?
R : Oui, l'équation d'Erwin Schrödinger utilisant la fonction d'onde d'Erwin Schrödinger est mathématiquement équivalente, mais elle est plus facile à utiliser à d'autres fins.
Q : Quel a été l'un des premiers succès de cette théorie ?
R : Un des premiers succès associés à cette théorie a été ce que l'on appelle aujourd'hui le principe d'incertitude d'Heisenberg.
Q : Qui a annoncé ce succès peu après sa mise au point ?
R : Werner Heisenberg lui-même a annoncé ce succès peu après sa mise au point.
Rechercher dans l'encyclopédie