Pesanteur
L'accélération que subit un objet en raison de la force gravitationnelle est appelée son accélération due à la gravité. Son unité SI est le m/s2. L'accélération due à la gravité est un vecteur, ce qui signifie qu'elle a à la fois une magnitude et une direction. L'accélération due à la gravité à la surface de la Terre est représentée par la lettre g. Elle a une valeur standard définie comme 9,80665 m/s2 (32,1740 ft/s2). Cependant, l'accélération réelle d'un corps en chute libre varie selon l'endroit.
Pourquoi les objets lourds ne tombent pas plus vite que les objets légers
Isaac Newton a calculé que la force résultante est égale à la masse multipliée par l'accélération, ou en symboles, F = m a



Examinez les exemples suivants :
a = 49 N 5 k g = 9,8 N / k g = 9,8 m / s 2 {\displaystyle a={\frac {49\,\mathrm {N} }{5\,\mathrm {kg} }\\ =9.8\,\mathrm {N/kg} =9.8\,\mathrm {m/s^{2}} }
a = 147 N 15 k g = 9,8 N / k g = 9,8 m / s 2 {\displaystyle a={\frac {147\,\mathrm {N} }{15\,\mathrm {kg} }\\ =9.8\,\mathrm {N/kg} =9.8\,\mathrm {m/s^{2}} }
Accélération de la surface
Selon l'endroit, un objet à la surface de la Terre tombe avec une accélération comprise entre 9,76 et 9,83 m/s2 (32,0 et 32,3 ft/s2).
La Terre n'est pas exactement sphérique. Elle ressemble à une sphère "écrasée", dont le rayon à l'équateur est légèrement plus grand que le rayon aux pôles. Cela a pour effet d'augmenter légèrement l'accélération gravitationnelle aux pôles (puisque nous sommes proches du centre de la Terre et que la force gravitationnelle dépend de la distance) et de la diminuer légèrement à l'équateur. De plus, en raison de l'accélération centripète, l'accélération due à la gravité est légèrement inférieure à l'équateur qu'aux pôles. Les changements dans la densité de la roche sous le sol ou la présence de montagnes à proximité peuvent affecter légèrement l'accélération gravitationnelle.
Altitude
L'accélération d'un objet change avec l'altitude. La variation de l'accélération gravitationnelle en fonction de la distance par rapport au centre de la Terre suit une loi de l'inverse du carré. Cela signifie que l'accélération gravitationnelle est inversement proportionnelle au carré de la distance par rapport au centre de la Terre. Lorsque la distance est doublée, l'accélération gravitationnelle diminue d'un facteur 4, lorsque la distance est triplée, l'accélération gravitationnelle diminue d'un facteur 9, et ainsi de suite.
accélération gravitationnelle ∝ 1 distance 2 {\displaystyle {\mbox{gravitational acceleration}}\ \propto \\\frac {1}{{\mbox{distance}}^{2}}}\ }
Accélération gravitationnelle × distance 2 = k
À la surface de la Terre, l'accélération due à la gravité est d'environ 9,8 m/s2 (32 ft/s2). La distance moyenne au centre de la Terre est de 6 371 km (3 959 mi).
k = 9,8 × 6371 2 {\displaystyle {k}={\mbox{9.8}}\ \ \times {{\mbox{6371}}^{2}}}
Utilisation de la constante k {\displaystyle k}
Accélération gravitationnelle = k distance 2
Exemple : Trouvez l'accélération due à la gravité à 1 000 km (620 mi) au-dessus de la surface de la Terre.
6371 + 1000 = 7371 {\style d'affichage 6371+1000=7371}
∴ La distance du centre de la Terre est de 7 371 km (4 580 mi).
accélération gravitationnelle = 9,8 × 6371 2 7371 2 ≈ 7.3 {\displaystyle {\mbox{gravitational acceleration}}\ ={\frac {{\mbox{9.8}}\ \times {{\mbox{6371}}^{2}}}{{\mbox{7371}}^{2}}}\ \ \approx 7.3}
∴ L'accélération due à la gravité à 1 000 km (620 mi) au-dessus de la surface de la Terre est de 7,3 m/s2 (24 ft/s2).
L'accélération gravitationnelle à la ligne de Kármán, la frontière entre l'atmosphère terrestre et l'espace extra-atmosphérique qui se trouve à une altitude de 100 km (62 mi), n'est que d'environ 3 % inférieure à celle du niveau de la mer.
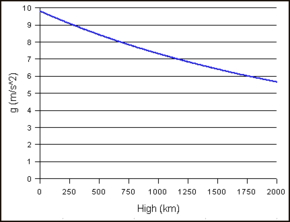
Modification de l'accélération gravitationnelle en fonction de la hauteur d'un objet
Questions et réponses
Q : Qu'est-ce que l'accélération due à la gravité ?
R : L'accélération due à la gravité est l'accélération subie par un objet sous l'effet de la force gravitationnelle.
Q : Quelle est l'unité SI de l'accélération due à la gravité ?
R : L'unité SI de l'accélération due à la gravité est le m/s2.
Q : L'accélération due à la gravité est-elle un scalaire ou un vecteur ?
R : L'accélération due à la pesanteur est un vecteur car elle possède à la fois une magnitude et une direction.
Q : Quel est le symbole utilisé pour représenter l'accélération due à la gravité à la surface de la Terre ?
R : Le symbole utilisé pour représenter l'accélération due à la gravité à la surface de la Terre est g.
Q : Quelle est la valeur standard de l'accélération due à la gravité à la surface de la Terre ?
R : La valeur standard de l'accélération due à la gravité à la surface de la Terre est de 9,80665 m/s2 (32,1740 ft/s2).
Q : L'accélération réelle d'un corps en chute libre varie-t-elle en fonction de l'endroit où il se trouve ?
R : Oui, l'accélération réelle d'un corps en chute libre varie en fonction du lieu.
Q : Quelle est la définition de l'accélération due à la gravité ?
R : L'accélération due à la gravité est l'accélération subie par un objet sous l'effet de la force gravitationnelle. Elle est représentée par la lettre g et a une valeur standard de 9,80665 m/s2 à la surface de la Terre, alors que l'accélération réelle peut varier en fonction de l'endroit.
Rechercher dans l'encyclopédie







