Logarithme

Histoire

Les logarithmes ont été utilisés pour la première fois en Inde au IIe siècle avant J.-C. Le premier à utiliser les logarithmes à l'époque moderne est le mathématicien allemand Michael Stifel (vers 1487-1567). En 1544, il écrivit les équations suivantes : q m q n = q m + n {\style d'affichage q^{m}q^{n}=q^{m+n}} et q m q n = q m - n {\style d'affichage {tfrac {q^{m}}{q^{n}}}=q^{m-n}} C'est la base de la compréhension des logarithmes. Pour le Stifel, m et n devaient être des nombres entiers. John Napier (1550-1617) ne voulait pas de cette restriction, et voulait une fourchette pour les exposants.

D'après Napier, les logarithmes expriment des rapports : a [style d'affichage a] a le même rapport à b [style d'affichage b], que c [style d'affichage c] à d [style d'affichage d] si la différence de leurs logarithmes correspond. Mathématiquement : log ( a ) - log ( b ) = log ( c ) - log ( d ) {\displaystyle \log(a)-\log(b)=\log(c)-\log(d)} . Au début, la base e a été utilisée (même si le numéro n'avait pas encore été nommé). Henry Briggs a proposé d'utiliser 10 comme base pour les logarithmes, de tels logarithmes sont très utiles en astronomie.

John Napier a travaillé sur les logarithmes

Relation avec les fonctions exponentielles

Un logarithme indique l'exposant (ou la puissance) nécessaire pour obtenir un certain nombre. Les logarithmes sont donc l'inverse (opposé) de l'exponentiation.

Tout comme une fonction exponentielle a trois parties, un logarithme a trois parties. Les trois parties d'un logarithme sont une base, un argument et une réponse (aussi appelée puissance).

Il s'agit d'une fonction exponentielle :

2 3 = 8 {\displaystyle 2^{3}=8\ }

Dans cette fonction, la base est 2, l'argument est 3 et la réponse est 8.

Cette fonction exponentielle a un inverse, son logarithme :

log 2 ( 8 ) = 3 {\displaystyle \log _{2}(8)=3\ }

Dans ce logarithme, la base est 2, l'argument est 8 et la réponse est 3.

Différence par rapport aux racines

L'addition a une opération inverse : la soustraction. De même, la multiplication a une opération inverse : la division. Par conséquent, il peut être difficile de comprendre pourquoi l'exponentiation a en fait deux opérations inverses : Pourquoi avons-nous besoin du logarithme s'il y a déjà la racine ? C'est le cas parce que l'exponentiation n'est pas commutative.

L'exemple suivant en est une illustration :

• Si vous avez x+2=3, vous pouvez alors utiliser la soustraction pour découvrir que x=3-2. C'est la même chose si vous avez 2+x=3 : vous obtenez également x=3-2. C'est parce que x+2 est égal à 2+x.
• Si vous avez x - 2=3, alors vous pouvez utiliser la division pour découvrir que x= 3 2 {\frac {3}{2}}} . C'est la même chose si vous avez 2 - x=3 : Vous obtenez également x= 3 2 {\textstyle {\frac {3}{2}}} . C'est parce que x - 2 est égal à 2 - x.
• Si vous avez x²=3, alors vous utilisez la racine (carrée) pour trouver x : Vous obtenez le résultat x = 3 {\textstyle {\sqrt {3}}} . Cependant, si vous avez 2x=3, alors vous ne pouvez pas utiliser la racine pour trouver x. Vous devez plutôt utiliser le logarithme (binaire) pour trouver x : Vous obtenez le résultat x=log2(3). En
   effet, 2x n'est généralement pas la même chose que x2 (par exemple, ²⁵⁼³² mais 5²=25).

Utilise

Les logarithmes peuvent faciliter la multiplication et la division de grands nombres, car l'addition de logarithmes équivaut à une multiplication, et la soustraction de logarithmes équivaut à une division.

Avant que les calculatrices ne deviennent populaires et courantes, les gens utilisaient des tableaux de logarithmes dans les livres pour multiplier et diviser. Les mêmes informations contenues dans un tableau de logarithmes étaient disponibles sur une règle à calcul, un outil sur lequel étaient écrits des logarithmes.

• Les spirales logarithmiques sont courantes dans la nature. On peut citer comme exemple la coquille d'un nautile ou la disposition des graines sur un tournesol.
• En chimie, le négatif du logarithme de la base 10 de l'activité des ions hydronium (H3O+, la forme que prend H+ dans l'eau) est la mesure connue sous le nom de pH. L'activité des ions hydronium dans l'eau neutre est de 10-7 mol/L à 25 °C, d'où un pH de 7 (ceci est le résultat de la constante d'équilibre, le produit de la concentration des ions hydronium et des ions hydroxyle, dans les solutions aqueuses étant de 10-14 M2).
• L'échelle de Richter mesure l'intensité des séismes sur une échelle logarithmique de base 10.
• En astronomie, la magnitude apparente mesure la luminosité des étoiles de façon logarithmique, puisque l'œil réagit également de façon logarithmique à la luminosité.
• Les intervalles musicaux sont mesurés de manière logarithmique en demi-tons. L'intervalle entre deux notes en demi-tons est le logarithme base 21/12 du rapport de fréquence (ou, de façon équivalente, 12 fois le logarithme base 2). Les demi-tons fractionnaires sont utilisés pour les tempéraments non égaux. En particulier pour mesurer les écarts par rapport à la gamme tempérée égale, les intervalles sont également exprimés en cents (centièmes d'un demi-ton tempéré égal). L'intervalle entre deux notes en cents est le logarithme base-21/1200 du rapport de fréquence (ou 1200 fois le logarithme base-2). En MIDI, les notes sont numérotées sur la gamme des demi-tons (hauteur nominale absolue logarithmique avec le do moyen à 60). Pour le microtuning à d'autres systèmes d'accord, une échelle logarithmique est définie, remplissant de manière compatible les intervalles entre les demi-tons de l'échelle tempérée égale. Cette gamme correspond aux numéros de note pour des demi-tons entiers. (voir microtuning en MIDI).

Logarithmes communs

Les logarithmes en base 10 sont appelés logarithmes communs. Ils sont généralement écrits sans la base. Par exemple :

log ( 100 ) = 2 {\displaystyle \log(100)=2\ }

Cela signifie que :

10 2 = 100 {\displaystyle 10^{2}=100\ }

Logarithmes naturels

Les logarithmes à la base e sont appelés logarithmes naturels. Le nombre e est proche de 2,71828, et est également appelé la constante eulérienne d'après le mathématicien Leonhard Euler.

Les logarithmes naturels peuvent prendre les symboles log e (x) (style d'affichage) log _{e}(x)\,} ou ln (x) (style d'affichage) ln (x)

Certains auteurs préfèrent l'utilisation de logarithmes naturels comme log ( x ), mais ils le mentionnent généralement dans les pages de préface.

Bases communes pour les logarithmes

base	abréviation	Commentaires
2	ld {\displaystyle \operatorname {ld} }	Très courant en informatique (binaire)
e	ln [style d'affichage] ou simplement log [style d'affichage].	Sa base est la constante e eulérienne. C'est le logarithme le plus communément utilisé en mathématiques pures.
10	log 10 {\displaystyle \log _{10}} ou log {\displaystyle \log } (parfois aussi écrit comme lg)	Utilisé dans certaines sciences comme la chimie et la biologie.
n'importe quel nombre, n	log n {\displaystyle \log _{n}}	Voici la manière générale d'écrire les logarithmes

Propriétés des logarithmes

Les logarithmes ont de nombreuses propriétés. Par exemple :

Propriétés de la définition d'un logarithme

Cette propriété est directement issue de la définition d'un logarithme :

log n ( n a ) = a {\displaystyle \log _{n}(n^{a})=a} Par exemple

log 2 ( 2 3 ) = 3 {\displaystyle \log _{2}(2^{3})=3} et

log 2 ( 1 2 ) = - 1 {\displaystyle \log _{2}{\bigg (}{\frac {1}{2}}{\bigg )}=-1} parce que 1 2 = 2 - 1 {\displaystyle \frac {1}{2}}=2^{-1}} .

Le logarithme à la base b d'un nombre a est le même que le logarithme de a divisé par le logarithme de b. C'est-à-dire,

log b ( a ) = log ( a ) log ( b ) {\displaystyle \log _{b}(a)={\frac {\log(a)}{\log(b)}}}

Par exemple, que a soit 6 et que b soit 2. Avec des calculatrices, nous pouvons montrer que cela est vrai ou du moins très proche :

log 2 ( 6 ) = log ( 6 ) log ( 2 ) {\style d'affichage \log _{2}(6)={\frac {\log(6)}{\log(2)}}}

log 2 ( 6 ) ≈ 2.584962 {\displaystyle \log _{2}(6)\approx 2.584962}

2.584962 ≈ 0.778151 0.301029 ≈ 2.584970 {\displaystyle 2.584962\approx {\frac {0.778151}{0.301029}}\approx 2.584970}

Nos résultats comportaient une petite erreur, mais celle-ci était due à l'arrondissement des chiffres.

Comme il est difficile d'imaginer le logarithme naturel, nous constatons que, en termes de logarithme base dix :

ln ( x ) = log ( x ) log ( e ) ≈ log ( x ) 0.434294 {\displaystyle \ln(x)={\frac {\log(x)}{\log(e)}}\approx {\frac {\log(x)}{0.434294}}} Où 0,434294 est une approximation pour le logarithme de e.

 

Opérations dans les arguments logarithmiques

Les logarithmes qui se multiplient à l'intérieur de leur argument peuvent être modifiés comme suit :

log ( a b ) = log ( a ) + log ( b ) {\displaystyle \log(ab)=\log(a)+\log(b)}

Par exemple,

log ( 1000 ) = log ( 10 ⋅ 10 ⋅ 10 ) = log ( 10 ) + log ( 10 ) + log ( 10 ) = 1 + 1 + 1 = 3 {\displaystyle \log(1000)=\log(10\cdot 10\cdot 10)=\log(10)+\log(10)+\log(10)+\log(10)=1+1+1=3}

Il en va de même pour la division mais la soustraction au lieu de l'addition, car c'est l'opération inverse de la multiplication :

log ( a b ) = log ( a ) - log ( b ) {\displaystyle \log {\bigg (}{\frac {a}{b}}{\bigg )}=\log(a)-\log(b)}

Tableaux de logarithmes, règles de calcul et applications historiques

Avant les ordinateurs électroniques, les logarithmes étaient utilisés tous les jours par les scientifiques. Les logarithmes ont aidé les scientifiques et les ingénieurs dans de nombreux domaines tels que l'astronomie.

Avant les ordinateurs, la table des logarithmes était un outil important. En 1617, Henry Briggs a imprimé la première table de logarithmes. C'était peu après l'invention de base de Napier. Plus tard, les gens ont fabriqué des tables avec une meilleure portée et une plus grande précision. Ces tableaux indiquaient les valeurs de logb(x) et bx pour tout nombre x dans une certaine plage, avec une certaine précision, pour une certaine base b (généralement b = 10). Par exemple, la première table de Briggs contenait les logarithmes communs de tous les nombres entiers dans la plage 1-1000, avec une précision de 8 chiffres. Comme la fonction f(x) = bx est la fonction inverse de logb(x), elle a été appelée l'antilogarithme. Les gens utilisaient ces tableaux pour multiplier et diviser des nombres. Par exemple, un utilisateur cherchait le logarithme dans le tableau pour chacun de deux nombres positifs. En additionnant les chiffres du tableau, on obtient le logarithme du produit. La fonction antilogarithme du tableau permet alors de trouver le produit en fonction de son logarithme.

Pour les calculs manuels qui nécessitent de la précision, la recherche des deux logarithmes, le calcul de leur somme ou de leur différence et la recherche de l'antilogarithme sont beaucoup plus rapides que la multiplication par les méthodes précédentes.

De nombreux tableaux de logarithmes donnent des logarithmes en fournissant séparément la caractéristique et la mantisse de x, c'est-à-dire la partie entière et la partie fractionnaire de log10(x). La caractéristique de 10 - x est un plus la caractéristique de x, et leurs signifiants sont les mêmes. Cela étend la portée des tableaux de logarithmes : étant donné un tableau énumérant les log10(x) pour tous les entiers x allant de 1 à 1000, le logarithme de 3542 est approximé par

log 10 ( 3542 ) = log 10 ( 10 ⋅ 354.2 ) = 1 + log 10 ( 354.2 ) ≈ 1 + log 10 ( 354 ) . {\displaystyle \log _{10}(3542)=\log _{10}(10\cdot 354.2)=1+\log _{10}(354.2)\approx 1+\log _{10}(354).\,}

Une autre application essentielle était la règle à calcul, une paire d'échelles divisées logarithmiquement utilisées pour le calcul, comme illustré ici :

Les nombres sont marqués sur des échelles mobiles à des distances proportionnelles aux différences entre leurs logarithmes. Faire glisser l'échelle supérieure de manière appropriée revient à ajouter mécaniquement des logarithmes. Par exemple, en ajoutant la distance de 1 à 2 sur l'échelle inférieure à la distance de 1 à 3 sur l'échelle supérieure, on obtient un produit de 6, qui est lu dans la partie inférieure. De nombreux ingénieurs et scientifiques ont utilisé des règles à calcul jusqu'aux années 1970. Les scientifiques peuvent travailler plus rapidement en utilisant une règle à calcul qu'en utilisant un tableau de logarithmes.

Représentation schématique d'une règle à calcul. En partant de 2 sur l'échelle inférieure, ajoutez la distance à 3 sur l'échelle supérieure pour atteindre le produit 6. La règle à calcul fonctionne parce qu'elle est marquée de telle sorte que la distance de 1 à x est proportionnelle au logarithme de x.


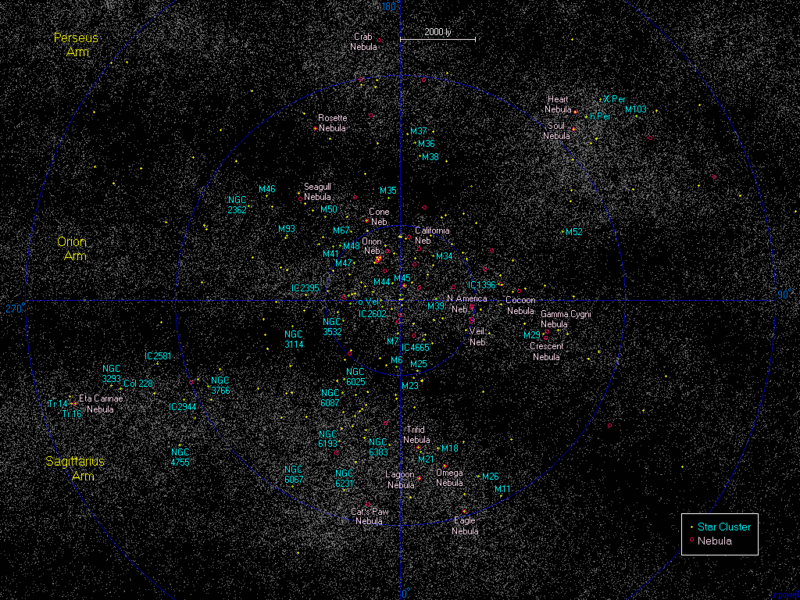
Les nébuleuses et amas d'étoiles les plus proches (carte cliquable)