Horloge lumineuse

L'horloge lumineuse est un moyen simple de montrer une caractéristique fondamentale de la relativité restreinte. Une horloge est conçue pour fonctionner en faisant rebondir un flash de lumière sur un miroir distant et en utilisant son retour pour déclencher un autre flash de lumière, tout en comptant le nombre de flashes qui se sont produits en cours de route. Il est facile de montrer que les habitants de la Terre qui regardent un vaisseau spatial voler au-dessus d'eux avec une telle horloge verraient son tic-tac relativement lent. Cet effet est appelé dilatation du temps.

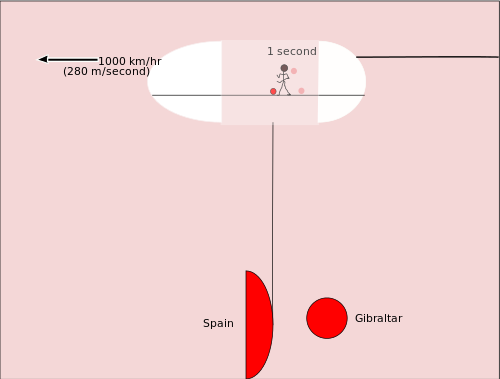
Avant d'étudier l'horloge lumineuse, examinons un autre type de relativité. Imaginez que quelqu'un dribble un ballon de basket dans la soute d'un gros avion-cargo. Le joueur de basket-ball se déplace dans la même direction que l'avion à réaction. Les autres personnes dans l'avion le voient se déplacer d'un mètre ou deux pendant qu'il fait un dribble. Entre le moment où le ballon rebondit la première fois et celui où il rebondit la deuxième fois, environ une seconde s'est écoulée. Mais quand le premier rebond s'est produit, le ballon de basket était au-dessus de Gibraltar, et quand le deuxième rebond s'est produit, le ballon de basket était au-dessus de l'eau, plus près de l'Espagne. Le ballon de basket s'est donc déplacé de 280 mètres par rapport à la Terre.

Examinons maintenant une question quelque peu similaire de mouvement relatif. Cette fois, nous allons examiner ce que les gens qui regardent les étoiles du pôle Nord voient lorsqu'un vaisseau spatial très rapide les survole. Nous pouvons utiliser l'algèbre et le théorème de Pythagore pour calculer combien de temps ralentit le vaisseau spatial. La seule autre chose dont nous avons besoin est l'équation qui relie la distance, d, le taux ou la vitesse de déplacement, r, et le temps, t. L'équation est :

d = rt

La vitesse de la lumière étant constante, nous allons appliquer cette valeur à deux problèmes. Nous appellerons la vitesse de la lumière c, car c'est la lettre que les scientifiques utilisent habituellement pour la nommer.

Une horloge est fabriquée en plaçant une sortie de lumière au bas d'un long poteau, un miroir au sommet du poteau et un détecteur de lumière électronique au bas du poteau. L'horloge est démarrée en fermant brièvement un interrupteur qui envoie un clignement de lumière du bas du poteau vers le haut du poteau où il est réfléchi vers le bas du poteau. Lorsque le détecteur de lumière situé au bas du poteau voit le clignotement de la lumière, il fait deux choses. Il en ajoute un au compteur qui y est fixé et il envoie un autre clignement de lumière vers le miroir. Lorsque ce clignotement de lumière revient vers le bas, le compteur passe à deux et un autre clignotement de lumière est déclenché. Comme la lumière se déplace très rapidement (300 000 km/seconde), pour chaque seconde mesurée par une horloge ordinaire, l'horloge lumineuse "fait tic-tac" un très grand nombre de fois.

Pour faciliter le calcul, nous dirons que le poteau fait un demi-kilomètre de long. Donc, si nous nous tenons près de l'horloge lumineuse qui est construite à côté du grand télescope au pôle Nord, nous verrons que la lumière voyage un kilomètre pour chaque "tic-tac" de l'horloge lumineuse. Puisque la distance parcourue, d, est égale à la vitesse multipliée par le temps, et que la vitesse impliquée est c, nous avons l'équation :

d = ct

et nous pouvons résoudre cette équation pour t afin d'apprendre combien de temps en secondes chaque "tick" est.

1 km = 300 000 km/seconde * t secondes

t secondes = 1 km/300 000 (km/seconde) = 1/300 000 secondes = 0,00000333...3 secondes

En d'autres termes, chaque "tic-tac" de l'horloge lumineuse prendra 0,00000333...3 secondes.

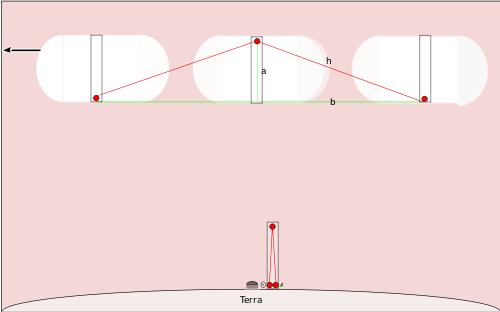
Si un vaisseau spatial volait sur une ligne droite passant au-dessus du pôle Nord à une grande fraction de la vitesse de la lumière, et qu'il avait une horloge similaire, les gens qui regardaient son passage verraient que le miroir au sommet du pôle s'était déplacé de directement au-dessus de la lumière émettrice, donc la lumière se déplacerait le long de la ligne marquée h dans le diagramme, et ensuite elle suivrait l'autre hypoténuse jusqu'à la base du pôle -- qui se serait maintenant déplacé d'une certaine distance puisque le vaisseau spatial se déplace si vite. Nous pouvons calculer le temps que prendrait une tique selon les habitants de la Terre. Nous savons que le pôle du vaisseau spatial a une longueur de a puisqu'il s'agit du même type d'horloge que celle que les gens utilisent au pôle Nord. Nous voulons calculer le temps qu'il faut pour faire un tic-tac de l'horloge du vaisseau spatial.

Nous savons que le vaisseau spatial va parcourir 1/2 r t' pendant que le clignement de la lumière se dirige vers le miroir, et un autre 1/2 r t' pendant que le clignement de la lumière se dirige vers la base du pôle. Ce calcul nous donne donc la longueur de la ligne b du graphique. Nous connaissons a, donc nous pouvons déterminer h par le théorème de Pythagore :

h = √(a2 + (rt' /2)²)

La distance totale parcourue par la lumière est donc de 2 h ou d = 2 √(a2 + (rt' /2)²)

Nous savons également que la vitesse de la lumière, c, est constante. Peu importe qui la mesure, il s'avère que c'est la même vitesse. Nous pouvons donc utiliser ce fait pour obtenir une autre façon de calculer le temps nécessaire à l'éclair de lumière pour aller de la base au sommet du poteau et vice-versa :

t' = d/c

En d'autres termes, d = c t' .

Nous pouvons donc écrire

c t' = 2 √(a2 + (rt' /2)²)

1/2 c t' = √(a2 + (rt' /2)²)

Pour résoudre l'équation ci-dessus, nous devrons le faire :

Carré des deux côtés
Diviser les deux côtés par t' ²
Multipliez les deux côtés par 4
Diviser les deux côtés par c2
Simplifier c2 / c2
Soustraire r2/c2 des deux côtés
Prendre la racine carrée des deux côtés
Multipliez les deux côtés par t'.
Diviser les deux côtés par √(1-r2/c2)

En résolvant l'équation ci-dessus, nous constatons que :

t' = 2a/(c√(1-r2/c2)

Au pôle Nord, le temps entre deux tics sur l'horloge est de 2a/c, ce qui nous permet d'écrire :

t' = t/√(1-r2/c2)

Si t = 1 seconde, alors si le vaisseau spatial se déplace à la moitié de la vitesse de la lumière, t' = 1,1547 sec.

Expérimentez différentes vitesses de déplacement à l'adresse suivante : http://www.1728.org/reltivty.htm

Questions et réponses

Q : Qu'est-ce qu'une cloche lumineuse ?

R : Une horloge lumineuse est un dispositif conçu pour démontrer une propriété fondamentale de la relativité restreinte. Il fonctionne en réfléchissant un éclair de lumière à partir d'un miroir distant et en utilisant son retour pour déclencher un autre éclair de lumière, tout en comptant combien d'éclairs se sont produits en chemin.

Q : Qu'est-ce que la dilatation du temps ?

R : La dilatation du temps est un phénomène qui se produit lorsque des personnes sur Terre regardent un vaisseau spatial voler au moyen d'une horloge lumineuse. Ils la voient faire un tic-tac relativement lent sous l'influence de la relativité.

Q : Comment pouvons-nous calculer combien le temps ralentit dans un vaisseau spatial ?

R : Nous pouvons utiliser l'algèbre et le théorème de Pythagore pour calculer combien le temps ralentit dans un vaisseau spatial. Nous devons appliquer l'équation d = rt (la distance est égale à la vitesse multipliée par le temps) et utiliser la vitesse constante de la lumière c dans deux problèmes.

Q : Comment fonctionne une horloge lumineuse ?

R : Une horloge lumineuse se compose d'une source de lumière au bas d'une longue tige avec un miroir en haut et un détecteur électronique en bas. Lorsqu'il est allumé, un seul flash de lumière passe du bas vers le haut, où il est réfléchi vers le bas lorsqu'il est détecté par le détecteur du bas, ce qui ajoute un compteur au compteur attaché et déclenche à nouveau un flash vers le haut. Ce processus se poursuit jusqu'à ce qu'il soit arrêté ou réinitialisé.

Q : De quelle équation avons-nous besoin pour ce calcul ?

R : Nous avons besoin de t' = 2a/(c√(1-r2/c2)), où t' (le temps entre les tics de l'horloge du pôle Nord) est égal à 2a/c divisé par √(1-r2/c2). Si t = 1 seconde, et en se déplaçant à la moitié de la vitesse de la lumière, t' = 1,1547 seconde.

Q. Quel est le rapport entre le théorème de Pythagore et ce calcul ?

R : Le théorème de Pythagore nous aide à trouver h (l'hypoténuse), qui fait partie de l'équation qui nous permet de calculer la durée de chaque tic en secondes (d=ct). Une fois que nous connaissons h, nous pouvons résoudre t', qui nous indique combien de temps dure chaque point selon les personnes sur la Terre qui regardent depuis le pôle Nord et les personnes sur le navire lui-même, qui passe au-dessus d'eux très rapidement.