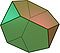
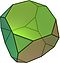
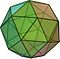
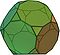
Solide d'Archimède

En géométrie, un solide d'Archimède est une forme convexe qui est composée de polygones. C'est un polyèdre, qui présente les propriétés suivantes :

Chaque visage est constitué d'un polygone régulier
Tous les coins de la forme se ressemblent
La forme n'est ni un solide platonique, ni un prisme, ni un antiprisme.

Selon le mode de comptage, il y a treize ou quinze formes de ce type. Sur deux de ces formes, il existe deux versions, qui ne peuvent pas être rendues congruentes par rotation. Les solides d'Archimède portent le nom du mathématicien grec Archimède, qui les a probablement découverts au 3e siècle avant Jésus-Christ. Les écrits d'Archimède ont été perdus, mais Pappus d'Alexandrie les a résumés au 4e siècle. Pendant la Renaissance, les artistes et les mathématiciens ont valorisé les formes pures et ont redécouvert toutes ces formes. Johannes Kepler a probablement terminé cette recherche vers 1620.

Pour construire un solide d'Archimède, il faut au moins deux polygones différents.

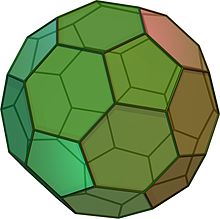
Un icosaèdre tronqué ressemble à un ballon de football. Il est composé de 12 pentagones équilatéraux et de 20 hexagones réguliers. Il a 60 sommets et 90 arêtes. C'est un solide d'Archimède

Propriétés

Les solides d'Archimède sont constitués de polygones réguliers, donc tous les bords ont la même longueur.
Tous les solides d'Archimède peuvent être produits à partir de solides de Platon, en "coupant les bords" du solide de Platon.
Le type de polygones se rencontrant à un coin ("vertex") caractérise à la fois le solide archimédien et platonique

Relation avec les solides de Platon

Les solides de Platon peuvent être transformés en solides d'Archimède en suivant une série de règles pour leur construction.

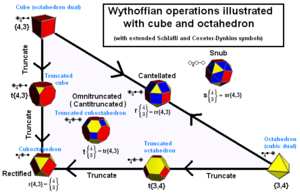
Les solides d'Archimède peuvent être construits comme des positions de générateur dans un kaléidoscope

Liste des solides d'Archimède

Voici une liste de tous les solides d'Archimède

Image	Nom	Visages	Tapez	Edges	Vertices
	Tétraèdre tronqué	8	4 triangles 4 hexagones	18	12
	Cuboctaèdre	14	8 triangles 6 carrés	24	12
	Cube tronqué	14	8 triangles 6 octogones	36	24
	Octaèdre tronqué	14	6 carrés 8 hexagones	36	24
	Rhombicuboctaèdre	26	8 triangles 18 carrés	48	24
	Cuboctaèdre tronqué	26	12 carrés 8 hexagones 6 octogones	72	48
	Snub cube (2 versions en miroir)	38	32 triangles 6 carrés	60	24
	Icosidodecahedron	32	20 triangles 12 pentagones	60	30
	Dodécaèdre tronqué	32	20 triangles 12 décagons	90	60
	Icosaèdre tronqué	32	12 pentagones 20 hexagones	90	60
	Rhombicosidodecahedron	62	20 triangles30 carrés12 pentagones	120	60
	Icosidodécaèdre tronqué	62	30 carrés 20 hexagones 12 décagons	180	120
	Snub dodécaèdre (2 versions en miroir)	92	80 triangles 12 pentagones	150	60

Questions et réponses

Kysymys: Mikä on arkimedealainen kiinteä kappale?

V: Arkhimedealainen kappale on monikulmioista koostuva kupera muoto, jonka ominaisuuksiin kuuluu, että jokainen pinta on säännöllinen monikulmio, kaikki kulmat näyttävät samalta ja että se ei ole platoninen kappale, prisma tai antiprisma.

Kysymys: Kuinka monta arkimedealaista kiinteää ainetta on olemassa?

V: Riippuen siitä, miten ne lasketaan, arkimedealaisia kiinteitä aineita on joko kolmetoista tai viisitoista.

K: Kuka löysi arkimedealaiset kiinteät kappaleet?

V: Arkhimedeen kiinteät kappaleet on nimetty muinaiskreikkalaisen matemaatikon Arkhimedeen mukaan, joka todennäköisesti löysi ne 3. vuosisadalla eaa.

K: Mitä Pappus Aleksandrialainen teki Arkhimedeen kirjoituksilla?

V: Pappus Aleksandrialainen teki yhteenvedon Arkhimedeen kiinteitä aineita koskevista Arkhimedeen kirjoituksista 4. vuosisadalla.

K: Miksi taiteilijat ja matemaatikot löysivät arkimedealaiset kiinteät kappaleet uudelleen renessanssin aikana?

V: Renessanssin aikana taiteilijat ja matemaatikot arvostivat puhtaita muotoja, ja Arkhimedeen kiinteitä aineita pidettiin puhtaina muotoina.

K: Milloin Johannes Kepler sai päätökseen kaikkien arkimedealaisten kiinteiden kappaleiden etsimisen?

V: Johannes Kepler sai todennäköisesti päätökseen kaikkien arkimedealaisten kiinteiden kappaleiden etsimisen noin vuonna 1620.

K: Mitä tarvitaan arkimedeeläisen kiinteän kappaleen rakentamiseen?

V: Arkhimedeen kiinteän kappaleen rakentamiseen tarvitaan vähintään kaksi erilaista monikulmiota.