Lois de Kepler
Les lois de Kepler sur le mouvement des planètes sont trois lois qui décrivent le mouvement des planètes autour du soleil :
- Les planètes se déplacent autour du soleil selon des orbites elliptiques. Le soleil se trouve dans l'un des deux foyers de l'orbite.
- Un segment de ligne joignant une planète et le Soleil balaye des zones égales pendant des intervalles de temps égaux.
- Le carré de la période orbitale d'une planète est proportionnel au cube du demi-grand axe de son orbite.
Johannes Kepler a trouvé ces lois, entre 1609 et 1619.
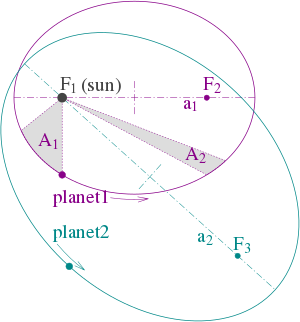
Figure 1 : Illustration des trois lois de Kepler avec deux orbites planétaires. (1) Les orbites sont des ellipses, avec des points focaux ƒ1 et ƒ2 pour la première planète et ƒ1 et ƒ3 pour la seconde. Le Soleil est placé au point focal ƒ1. (2) Les deux secteurs ombragés A1 et A2 ont la même surface et le temps nécessaire à la planète 1 pour couvrir le segment A1 est égal au temps nécessaire pour couvrir le segment A2. (3) Les temps totaux d'orbite de la planète 1 et de la planète 2 ont un rapport a13/2 : a23/2.
Comparaison avec Copernic
Les lois de Kepler améliorent le modèle de Copernic. Si les excentricités des orbites des planètes sont prises comme zéro, alors Kepler est fondamentalement d'accord avec Copernic :
- L'orbite planétaire est un cercle
- Le Soleil au centre de l'orbite
- La vitesse de la planète en orbite est constante
Les excentricités des orbites des planètes connues de Copernic et de Kepler sont faibles, de sorte que les règles ci-dessus donnent de bonnes approximations du mouvement des planètes ; mais les lois de Kepler correspondent mieux aux observations que celles de Copernic.
Les corrections de Kepler ne sont pas du tout évidentes :
- L'orbite de la planète n'est pas un cercle, mais une ellipse.
- Le Soleil n'est pas au centre mais à un point focal de l'orbite elliptique.
- Ni la vitesse linéaire ni la vitesse angulaire de la planète en orbite ne sont constantes, mais la vitesse de surface est constante.
L'excentricité de l'orbite de la Terre rend le temps de l'équinoxe de mars à l'équinoxe de septembre, environ 186 jours, inégal au temps de l'équinoxe de septembre à l'équinoxe de mars, environ 179 jours. Un diamètre couperait l'orbite en parties égales, mais le plan passant par le soleil et parallèle à l'équateur de la terre coupe l'orbite en deux parties avec des surfaces dans un rapport de 186 à 179, de sorte que l'excentricité de l'orbite de la terre est d'environ
ε ≈ π 4 186 - 179 186 + 179 ≈ 0.015 , {\displaystyle \varepsilon \approx {\frac {pi }{4}}{\frac {186-179}{186+179}}\approx 0.015,}
qui est proche de la valeur correcte (0,016710219) (voir l'orbite de la Terre). Le calcul est correct lorsque le périhélie, la date à laquelle la Terre est la plus proche du Soleil, tombe sur un solstice. Le périhélie actuel, proche du 4 janvier, est assez proche du solstice du 21 décembre
Rechercher dans l'encyclopédie
