Inégalité (mathématiques)

Travailler avec les inégalités

L'inégalité en mathématiques est la comparaison de deux solutions ou réponses par plus ou moins que. C'est lorsque les deux solutions ou encore plusieurs solutions comparées ne sont pas de même valeur. Résoudre une inégalité, c'est trouver ses solutions. Lorsque vous substituez un nombre à une variable et que l'énoncé est vrai, il s'agit alors d'une solution. Lorsque vous substituez un nombre à une variable et que l'énoncé n'est pas vrai, le nombre n'est pas une solution à l'énoncé.

L'inégalité consiste à trouver une solution à une variable donnée. C'est trouver un ordre relatif d'un ensemble. L'inégalité a de nombreuses solutions, mais il faut trouver les vraies solutions. L'inégalité consiste à résoudre des nombres réels. La bonne façon de lire l'inégalité est de gauche à droite, tout comme les autres équations, mais la seule différence est qu'elles ont des règles différentes pour chaque équation.

Par exemple, x+4>12, où x est un nombre réel. En premier lieu, une personne doit trouver le x et elle doit savoir s'il s'agit d'une solution. La réponse sera x>8 et il s'agit d'une affirmation vraie. Cette expression concerne l'emplacement de x dans l'ensemble des nombres réels. Une ligne de nombres est une façon de montrer la position par rapport à tous les autres nombres réels (voir figure Inégalité 1).

Inégalité 1 C'est la solution pour l'équation x+4>12

Différents types d'inégalités

Il existe cinq types d'inégalités différentes :

1. La première est celle des inégalités linéaires, c'est-à-dire une inégalité qui différencie les expressions par soit moins que ou égal à, moins que ou plus que ou égal à, plus que. Si nous remplaçons l'inégalité par la relation d'égalité, le résultat sera alors une équation linéaire.
2. La seconde est la combinaison des inégalités qui doit satisfaire les inégalités, vous devez avoir un nombre dans les ensembles de solutions pour que les nombres satisfaisant les inégalités soient les valeurs au croisement des deux ensembles de solutions.
3. Le troisième est celui des inégalités impliquant des valeurs absolues, ce qui signifie que les valeurs peuvent être reformulées comme des combinaisons d'inégalités qui impliqueront des valeurs absolues.
4. La quatrième est appelée inégalités polynomiales, ce qui signifie qu'elle est continue, que leurs graphiques ne comportent pas de sauts ou de ruptures.
5. Enfin et surtout, il y a les inégalités rationnelles, c'est-à-dire la forme d'un des polynômes divisée par un polynôme. En d'autres termes, les graphes des fonctions rationnelles n'ont pas de ruptures et ne représentent pas les zéros du dénominateur.

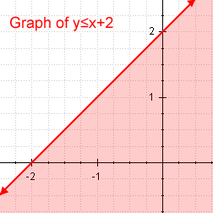
Inégalité linéaire Exemple d'inégalité linéaire


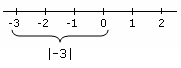
valeur absolue Exemple qui montre la valeur absolue

Quatre façons de résoudre les inégalités

Il y a quatre façons de résoudre les équations quadratiques :

1. La règle numéro un est que vous devez ajouter ou soustraire le même nombre des deux côtés.
2. La règle numéro deux est qu'il faut changer les côtés et changer le positionnement du signe de l'inégalité.
3. La règle numéro trois est qu'il faut multiplier.
4. La règle numéro quatre consiste à diviser le même nombre positif ou négatif dans les deux camps. Mais, vous ne pouvez les utiliser que pour les problèmes d'inégalité faciles.

En outre, elle prendra deux mesures pour résoudre une inégalité. La première consiste à simplifier en utilisant la réciproque de l'addition ou de la soustraction. La seconde consiste à simplifier davantage en utilisant la réciproque de multiplication ou de division. Lorsque vous multipliez ou divisez une inégalité par un nombre négatif, n'oubliez pas de tourner le symbole d'inégalité.

Un exemple d'ajout d'inégalités.


exemple de multiplication de l'inégalité

Exemples de solutions aux inégalités

L'inégalité est une affirmation mathématique qui explique que les deux valeurs ne sont pas égales et différentes. L'équation ab signifie que a n'est pas égal à b. L'inégalité est la même dans toutes les équations, mais la seule différence est que l'inégalité n'utilise pas un signe égal, mais des symboles. L'inégalité b>a représente que b est plus grand que a. Les limites de vitesse, le marquage et d'autres utilisent l'inégalité pour les exprimer.

Pour résoudre une inégalité, une personne doit avoir une déclaration véridique. Lorsque vous divisez ou multipliez une inégalité par un nombre négatif des deux côtés, la déclaration est fausse. Pour que la déclaration soit correcte avec un nombre négatif, vous devez inverser le symbole pour qu'elle soit correcte. Lorsqu'un nombre est un nombre positif, vous n'avez pas besoin d'inverser le symbole. L'inégalité consiste à faire une déclaration vraie.

Par exemple, commencez par une déclaration véridique -6y<-12. Lorsque les deux côtés sont divisés par -6, le résultat devient y<2. Dans cet énoncé, le symbole doit être inversé pour obtenir un énoncé vrai, y>2 est la bonne réponse. Dans la ligne des nombres (voir figure Inégalité 2), un cercle fermé et ombragé indique qu'il est inclus dans l'ensemble des solutions. Un cercle ouvert indique qu'il n'est pas inclus dans l'ensemble de solutions.

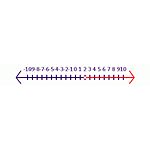
Inégalité 2 Solution pour l'équation -6y<-12

Pages connexes

• Égalité (mathématiques)
• Équation