Le théorème du schéma de Holland

Le théorème du schéma de Holland, également appelé théorème fondamental des algorithmes génétiques, est une inégalité qui résulte de l'élaboration d'une équation à gros grains pour la dynamique de l'évolution. Selon le théorème du schéma, les schémas courts d'ordre inférieur dont l'aptitude est supérieure à la moyenne augmentent de façon exponentielle en fréquence au cours des générations successives. Le théorème a été proposé par John Holland dans les années 1970. Il a d'abord été largement considéré comme le fondement des explications de la puissance des algorithmes génétiques. Toutefois, cette interprétation de ses implications a été critiquée dans plusieurs publications examinées dans , où le théorème du schéma est présenté comme un cas particulier de l'équation de prix avec la fonction d'indicateur du schéma comme mesure macroscopique.

Un schéma est un modèle qui identifie un sous-ensemble de chaînes de caractères présentant des similitudes à certaines positions. Les schémas sont un cas particulier des ensembles de cylindres, et forment donc un espace topologique.

Description

Le schéma 1*10*1 décrit l'ensemble de toutes les chaînes de longueur 6 avec des 1 aux positions 1, 3 et 6 et un 0 à la position 4. Le * est un symbole de remplacement, ce qui signifie que les positions 2 et 5 peuvent avoir une valeur de 1 ou de 0. L'ordre d'un schéma o ( H ) {\displaystyle o(H) $o(H)$ } est défini comme le nombre de positions fixes dans le modèle, tandis que la longueur de définition δ ( H ) {\displaystyle \delta (H)} $\delta (H)$ est la distance entre la première et la dernière position spécifique. L'ordre de 1*10*1 est 4 et sa longueur de définition est 5. L'adéquation d'un schéma est l'adéquation moyenne de toutes les chaînes correspondant au schéma. L'adéquation d'une chaîne est une mesure de la valeur de la solution codée du problème, telle que calculée par une fonction d'évaluation spécifique au problème. En utilisant les méthodes établies et les opérateurs génétiques des algorithmes génétiques, le théorème du schéma stipule que les schémas courts, d'ordre inférieur, dont l'aptitude est supérieure à la moyenne, augmentent de manière exponentielle au cours des générations successives. Exprimé sous la forme d'une équation :

E ( m ( H , t + 1 ) ) ≥ m ( H , t ) f ( H ) a t [ 1 - p ] . Nom de l'opérateur {E} (m(H,t+1))\geq {m(H,t)f(H) \over a_{t}}[1-p]. } $\operatorname {E} (m(H,t+1))\geq {m(H,t)f(H) \over a_{t}}[1-p].$

Ici, m ( H , t ) $m(H,t)$ est le nombre de chaînes de caractères appartenant au schéma H à la $H$ génération t $t$ f(H) $f(H)$ est l'aptitude moyenne observée du schéma H $H$ et a $a_{t}$ t est l'aptitude moyenne observée à la génération t $t$ . La probabilité de perturbation p {\displaystyle p} $p$ est la probabilité que le croisement ou la mutation détruise le schéma H {\displaystyle H} $H$ . Elle peut être exprimée sous la forme :

p = δ ( H ) l - 1 p c + o ( H ) p m {\displaystyle p={\delta (H) \over l-1}p_{c}+o(H)p_{m}} $p={\delta (H) \over l-1}p_{c}+o(H)p_{m}$

où o ( H ) $o(H)$ est l'ordre du schéma, l est la $l$ longueur du code, p m est la probabilité de mutation et p $p_{m}$ $p_{c}$ c est la probabilité de croisement. Ainsi, un schéma dont la longueur de définition est plus courte δ ( H )/style d'affichage \delta (H) $\delta (H)$ } est moins susceptible d'être perturbé.
Un point souvent mal compris est la raison pour laquelle le théorème du schéma est une inégalité plutôt qu'une égalité. La réponse est en fait simple : le théorème néglige la faible, mais non nulle, probabilité qu'une chaîne appartenant au schéma H soit créée "de toutes pièces" par mutation d'une seule chaîne (ou recombinaison de deux chaînes) qui n'appartenait pas au schéma $H$ $H$ H dans la génération précédente.

Limitation

Le théorème du schéma tient sous l'hypothèse d'un algorithme génétique qui maintient une population infiniment grande, mais ne se reporte pas toujours à la pratique (finie) : en raison d'une erreur d'échantillonnage dans la population initiale, les algorithmes génétiques peuvent converger sur des schémas qui n'ont pas d'avantage sélectif. Cela se produit notamment dans l'optimisation multimodale, où une fonction peut avoir plusieurs pics : la population peut dériver pour préférer l'un des pics, en ignorant les autres.

La raison pour laquelle le Schéma Théorème ne peut pas expliquer la puissance des algorithmes génétiques est qu'il s'applique à tous les cas de problèmes et ne peut pas faire la distinction entre les problèmes pour lesquels les algorithmes génétiques sont peu performants et ceux pour lesquels ils sont performants.

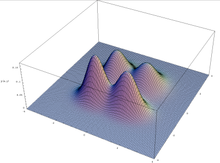
Tracé d'une fonction multimodale en deux variables.

Questions et réponses

Q : Qu'est-ce que le théorème du schéma de Holland ?

R : Le théorème du schéma de Holland est un théorème relatif aux algorithmes génétiques qui stipule que les individus dont l'aptitude est supérieure à la moyenne ont plus de chances de l'emporter.

Q : Qui a proposé le théorème du schéma de Holland et quand ?

R : John Holland a proposé le théorème du schéma de Holland dans les années 1970.

Q : Qu'est-ce qu'un schéma dans le contexte des algorithmes génétiques ?

R : Dans le contexte des algorithmes génétiques, un schéma est un modèle qui identifie un sous-ensemble de chaînes présentant des similitudes à certaines positions.

Q : Quelle est l'interprétation du théorème de Holland sur les schémas, qui a servi de base aux explications sur la puissance des algorithmes génétiques ?

R : L'interprétation du théorème du schéma de Holland, qui a servi de base aux explications de la puissance des algorithmes génétiques, est que les individus dont l'aptitude est supérieure à la moyenne ont plus de chances de l'emporter.

Q : Qu'est-ce que les critiques du théorème du schéma de Holland ont montré qu'il était ?

R : La critique du théorème des schémas de Holland a montré qu'il s'agissait d'un cas particulier de l'équation de prix avec la fonction d'indicateur de schéma comme mesure macroscopique.

Q : Qu'est-ce qu'un cas particulier de jeux de cylindres ?

R : Les schémas sont un cas particulier d'ensembles cylindriques.

Q : Quel type d'espace les schémas forment-ils ?

R : Les schémas forment un espace topologique.