Fonction de Heaviside
La fonction Heaviside, H est une fonction non continue dont la valeur est de zéro pour une entrée négative et de un pour une entrée positive.
Cette fonction est utilisée dans les mathématiques de la théorie du contrôle pour représenter un signal qui s'allume à un moment précis et reste allumé indéfiniment. Elle a été nommée d'après l'Anglais Oliver Heaviside.
La fonction Heaviside est l'intégrale de la fonction delta de Dirac : H′ = δ. Cela s'écrit parfois comme
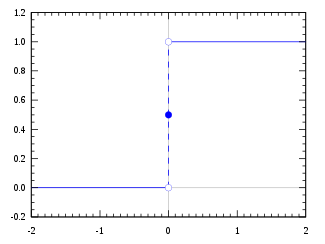
La fonction d'échelonnement Heaviside, utilisant la convention de demi-maximum
Forme discrète
Nous pouvons également définir une forme alternative de la fonction de Heaviside step en fonction d'une variable discrète n :
H [ n ] = { 0 , n < 0 1 , n ≥ 0 {\displaystyle H[n]={\begin{cases}0,&n<0\\1,&n\geq 0\end{cases}}}
où n est un nombre entier.
Ou
H ( x ) = lim z → x - ( ( | z | / z + 1 ) / 2 ) {\displaystyle H(x)=\lim _{z\rightarrow x^{-}}((|z|/z+1)/2)}
L'impulsion unitaire en temps discret est la première différence du pas de temps discret
δ [ n ] = H [ n ] - H [ n - 1 ] . {\displaystyle \delta \left[n\right]=H[n]-H[n-1] . }
Cette fonction est la somme cumulative du delta de Kronecker :
H [ n ] = ∑ k = - ∞ n δ [ k ] {\displaystyle H[n]=\sum _{k=-\infty }^{n}\delta [k]\,}
où
δ [ k ] = δ k , 0 {\displaystyle \delta [k]=\delta _{k,0}\,}
est la fonction d'impulsion de l'unité discrète.
Représentations
Souvent, une représentation intégrale de la fonction de l'escalier Heaviside est utile :
H ( x ) = lim ϵ → 0 + - 1 2 π i ∫ - ∞ ∞ 1 τ + i ϵ e - i x τ d τ = lim ϵ → 0 + 1 2 π i ∫ - ∞ ∞ 1 τ - i ϵ e i x τ d τ . {\displaystyle H(x)=\lim _{\epsilon \to 0^{+}}-{1 \over 2\pi \mathrm {i} }\int _{-\infty }^{\infty }{1 \over \tau +\mathrm {i} \epsilon }\mathrm {e} ^{-\mathrm {i} x\tau }\mathrm {d} \tau =\lim _{\epsilon \to 0^{+}}{1 \over 2\pi \mathrm {i} }\int _{-\infty }^{\infty }{1 \over \tau -\mathrm {i} \epsilon }\mathrm {e} ^{\mathrm {i} x\tau }\mathrm {d} \tau . }
H(0)
La valeur de la fonction à 0 peut être définie comme H(0) = 0, H(0) = ½ ou H(0) = 1.
H ( x ) = 1 + sgn ( x ) 2 = { 0 , x < 0 1 2 , x = 0 1 , x > 0. {\displaystyle H(x)={\frac {1+\operatorname {sgn}(x)}{2}}={\begin{cases}0,&x<0\\{\frac {1}{2}},&x=0\\\1,&x>0.\end{cases}}
Pages connexes
- Transformation de Laplace
Questions et réponses
Q : Qu'est-ce que la fonction de Heaviside ?
R : La fonction de Heaviside est une fonction non continue dont la valeur est de zéro pour une entrée négative et de un pour une entrée positive.
Q : Pourquoi la fonction de Heaviside est-elle utilisée en théorie du contrôle ?
R : La fonction de Heaviside est utilisée dans la théorie du contrôle pour représenter un signal qui s'allume à un moment donné et reste allumé indéfiniment.
Q : Qui est la personne qui a donné son nom à la fonction de Heaviside ?
R : La fonction de Heaviside a été nommée en l'honneur de l'Anglais Oliver Heaviside.
Q : Quelle est la relation entre la fonction de Heaviside et la fonction delta de Dirac ?
R : La fonction de Heaviside est l'intégrale de la fonction delta de Dirac : H′(x)= δ(x).
Q : Quelle est la sortie de la fonction de Heaviside pour des entrées positives ?
R : La fonction de Heaviside produit un pour les entrées positives.
Q : Que produit la fonction de Heaviside pour des entrées négatives ?
R : La fonction de Heaviside produit un zéro pour les entrées négatives.
Q : Quel type de fonction est la fonction de Heaviside ?
R : La fonction de Heaviside est une fonction non continue.
Rechercher dans l'encyclopédie
![{\displaystyle H[n]={\begin{cases}0,&n<0\\1,&n\geq 0\end{cases}}}](https://www.alegsaonline.com/image/efb65c686bdec46712eae1997c363f7ef8709b79.svg)

![{\displaystyle \delta \left[n\right]=H[n]-H[n-1].}](https://www.alegsaonline.com/image/e6c417f161a7987a4db18818743eeb23494b0feb.svg)
![{\displaystyle H[n]=\sum _{k=-\infty }^{n}\delta [k]\,}](https://www.alegsaonline.com/image/5db28db3163e2940aaf93d0fc180edb19d865d32.svg)
![{\displaystyle \delta [k]=\delta _{k,0}\,}](https://www.alegsaonline.com/image/97a99ab7d257c74f38fbb2d42c8e42e1cb16d0e9.svg)

