Loi de Gumbel
La distribution de Gumbel est une distribution de probabilité des valeurs extrêmes.
En théorie des probabilités et en statistique, la distribution de Gumbel est utilisée pour modéliser la distribution du maximum (ou du minimum) d'un certain nombre d'échantillons de différentes distributions.
Une telle distribution pourrait être utilisée pour représenter la distribution du niveau maximum d'une rivière pour une année donnée s'il existait une liste de valeurs maximales pour les dix dernières années. Elle est également utile pour prédire la probabilité qu'un tremblement de terre extrême, une inondation ou une autre catastrophe naturelle se produise.
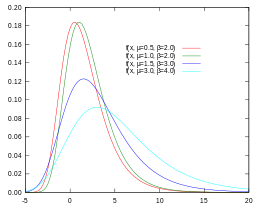
Fonction de distribution de probabilité de Gumbel (PDF)
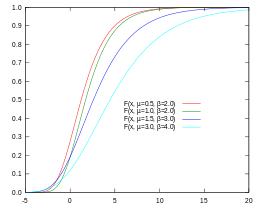
Fonction de distribution cumulative de Gumbel (CDF)
Propriétés
La distribution de Gumbel est une distribution de probabilité continue. Les distributions de Gumbel sont une famille de distributions de même forme générale. Ces distributions diffèrent par leur emplacement et leurs paramètres d'échelle : la moyenne ("average") de la distribution définit son emplacement, et l'écart-type ("variability") définit l'échelle.
On reconnaît la fonction de densité de probabilité de Gumbel (PDF) et la fonction de distribution cumulative de Gumbel (CDF).
Dans la PDF, la probabilité P qu'une valeur V se produise entre les limites A et B, brièvement écrite comme P(A<V<B), est trouvée par l'aire sous la courbe PDF entre A et B.
| Exemple de probabilité dans le PDF |
| Dans la figure de la fonction de densité de probabilité normale, les valeurs sur l'axe horizontal doivent se lire respectivement : μ-3σ, μ-2σ, μ-1σ, μ+1σ, μ+2σ et μ+3σ. μ = moyenne, σ = écart-type. |
Contrairement à la distribution normale, le PDF de Gumbel est a-symétrique et incliné vers la droite.
CDF
Dans la CDF, la probabilité qu'une valeur V soit inférieure à A se retrouve directement comme la valeur de la CDF à A :
P ( V ≤ A ) = C D F ( A ) {\displaystyle P(V\leq A)=CDF(A)}
| Exemple de probabilité dans la CDF |
| Dans la figure CDF de Gumbel, la courbe rouge indique que la probabilité que V soit inférieur à 5 est de 0,9 (ou 90%), alors que pour la ligne bleu foncé cette probabilité est de 0,7 ou 70%. |

La fonction de densité de probabilité normale (PDF) est symétrique.
Mathématiques
Le CDF
L'expression mathématique de la CDF est :
C D F ( A ) = e - e - ( A - μ ) / β , {\displaystyle CDF(A)=e^{-e^{-(A-\mu )/\beta }},}
où μ est le mode (la valeur où la fonction de densité de probabilité atteint son maximum), e est une constante mathématique, environ 2,718, et β est une valeur liée à l'écart type (σ) :
β = σ 6 / π , {\displaystyle \beta =\sigma {\sqrt {6}}/\pi ,}
où π est le symbole grec de Pi dont la valeur est proche de 22/7 ou de 3,142, et le symbole [displaystyle]
Mode et médiane
Le mode μ peut être trouvé à partir de la médiane M, qui est la valeur de A où CDF(A)=0,5, et β :
μ = M + β ln ( ln 2 ) , {\displaystyle \mu = M+\beta \ln \left(\ln 2\right),}
où ln est le logarithme naturel.
Moyenne
La moyenne, E(x), donnée par :
E ( x ) = μ + c β , {\displaystyle \operatorname {E} (x)=\mu +c\beta ,}
où c

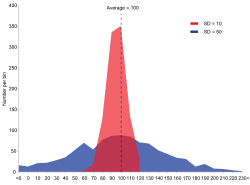
Il existe deux séries de données : le rouge et le bleu. Toutes deux ont la même moyenne (moyenne) : 100, mais le groupe bleu a un écart-type plus important (SD=σ=50) que le groupe rouge (SD=σ=10).
Estimation
Dans une série de données, le mode paramètres (μ) et β peut être estimé à partir de la moyenne, de la médiane et de l'écart-type. Le calcul des trois dernières quantités est expliqué dans les pages Wiki respectives. Ensuite, à l'aide des formules données dans la section précédente, les facteurs μ et β peuvent être calculés. De cette façon, la CDF de la distribution de Gumbel appartenant aux données peut être déterminée et la probabilité de valeurs intéressantes des données peut être trouvée.

A adapté la distribution cumulative de Gumbel aux précipitations maximales d'un jour en octobre en utilisant CumFreq
Candidature
En hydrologie, la distribution de Gumbel est utilisée pour analyser des variables telles que les valeurs maximales mensuelles et annuelles des précipitations quotidiennes et des volumes de débit des rivières, et aussi pour décrire les sécheresses.
L'image bleue illustre un exemple d'ajustement de la distribution de Gumbel à des précipitations maximales d'un jour en octobre classées, montrant également la ceinture de confiance de 90 % basée sur la distribution binomiale.
Questions et réponses
Q : Qu'est-ce que la distribution de Gumbel ?
R : La distribution de Gumbel est une distribution de probabilité de valeurs extrêmes.
Q : À quoi sert la distribution de Gumbel ?
R : La distribution de Gumbel est utilisée pour modéliser la distribution du maximum (ou du minimum) d'un certain nombre d'échantillons de diverses distributions.
Q : Comment la distribution de Gumbel peut-elle être utilisée pour prévoir les catastrophes naturelles ?
R : La distribution de Gumbel est utile pour prédire la probabilité qu'un tremblement de terre extrême, une inondation ou une autre catastrophe naturelle se produise.
Q : Quel est un exemple d'utilisation de la distribution de Gumbel pour représenter un événement passé ?
R : La distribution de Gumbel pourrait être utilisée pour représenter la distribution du niveau maximal d'une rivière au cours d'une année donnée si l'on disposait d'une liste des valeurs maximales pour les dix dernières années.
Q : La distribution de Gumbel n'est-elle utile que pour prévoir les catastrophes naturelles ?
R : Non, la distribution de Gumbel peut être utilisée pour modéliser la distribution des valeurs extrêmes dans n'importe quelle situation.
Q : La distribution de Gumbel peut-elle être utilisée pour modéliser la valeur minimale d'un ensemble d'échantillons ?
R : Oui, la distribution de Gumbel peut être utilisée pour modéliser la distribution du maximum ou du minimum d'un ensemble d'échantillons.
Q : La distribution de Gumbel est-elle une distribution couramment utilisée en théorie des probabilités et en statistique ?
R : Oui, la distribution de Gumbel est une distribution couramment utilisée en théorie des probabilités et en statistique, notamment pour modéliser les valeurs extrêmes.
Rechercher dans l'encyclopédie



