Coloration de graphe
La coloration des graphiques est le nom d'un certain nombre de problèmes issus de la théorie des graphiques. Ces problèmes concernent la coloration (ou l'étiquetage) des sommets d'un graphique, sous certaines conditions. Un problème simple dans ce contexte pourrait chercher le nombre minimal de couleurs nécessaires pour colorer les sommets, lorsque deux sommets connectés ne peuvent pas avoir la même couleur. Dans le graphique présenté, les cercles sont appelés sommets et les lignes qui les relient sont appelées arêtes. Le nombre minimum de couleurs nécessaires pour colorier un graphique est appelé son nombre chromatique.
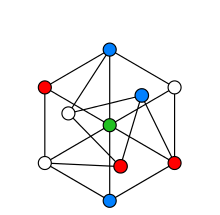
Une solution valable de coloration d'un graphique, lorsque deux sommets connectés ne doivent pas avoir la même couleur.
Questions et réponses
Q : Qu'est-ce que la coloration des graphes ?
R : La coloration des graphes est un problème de la théorie des graphes qui consiste à colorer ou étiqueter les sommets d'un graphe selon certaines conditions.
Q : Qu'est-ce qu'un problème simple dans le contexte de la coloration des graphes ?
R : Un problème simple peut consister à trouver le nombre minimum de couleurs nécessaires pour colorer les sommets d'un graphe, tout en s'assurant que deux sommets connectés n'ont pas la même couleur.
Q : Comment s'appellent les cercles d'un graphe ?
R : Les cercles d'un graphique s'appellent les sommets.
Q : Comment appelle-t-on les lignes qui relient les cercles d'un graphique ?
R : Les lignes reliant les cercles d'un graphique sont appelées des arêtes.
Q : Comment appelle-t-on le nombre minimum de couleurs nécessaires pour colorer un graphique ?
R : Le nombre minimum de couleurs nécessaires pour colorer un graphique est appelé nombre chromatique.
Q : Quel est le but de la coloration des graphes ?
R : Le but de la coloration des graphes est de trouver des solutions aux problèmes de la théorie des graphes qui impliquent de colorer ou d'étiqueter les sommets d'un graphe selon certaines conditions.
Q : Pourquoi la coloration des graphes est-elle importante ?
R : La coloration des graphes est importante dans divers domaines, notamment l'informatique, la physique et les sciences sociales, et peut être utilisée pour modéliser des problèmes réels tels que l'ordonnancement, l'allocation des ressources et l'optimisation des réseaux.
Rechercher dans l'encyclopédie