Nombre d'or
Avec un chiffre a et un autre chiffre plus petit b, on trouve le rapport des deux chiffres en les divisant. Leur rapport est a/b. Un autre rapport est obtenu en additionnant les deux nombres a+b et en divisant ce résultat par le plus grand nombre a. Le nouveau rapport est (a+b)/a. Si ces deux rapports sont égaux au même nombre, alors ce nombre est appelé le nombre d'or. La lettre grecque φ {\displaystyle \varphi }
(phi) est généralement utilisé comme le nom du nombre d'or.
Par exemple, si b = 1 et a/b = φ {\displaystyle \varphi } , puis a = φ {\displaystyle \varphi } . Le deuxième rapport (a+b)/a est alors ( φ + 1 ) / φ {\displaystyle (\varphi +1)/\varphi }
. Comme ces deux ratios sont égaux, c'est vrai :
φ = φ + 1 φ {\displaystyle \varphi ={\frac {\varphi +1}{\varphi }}}
Une façon d'écrire ce numéro est
φ = 1 + 5 2 {\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}}
5 {\displaystyle {\sqrt {5}}}
est comme un nombre quelconque qui, multiplié par lui-même, donne 5 (ou quel nombre est multiplié) : 5 × 5 = 5 {\displaystyle {\sqrt {5}}\times {\sqrt {5}}=5}
.
Le nombre d'or est un nombre irrationnel. Si une personne essaie de l'écrire, il ne s'arrêtera jamais et ne fera jamais un motif, mais il commencera de cette façon : 1,6180339887... Ce qui est important avec ce nombre, c'est qu'une personne peut en soustraire 1 ou le diviser par 1. Dans les deux cas, le nombre continuera à avancer et ne s'arrêtera jamais.
Rectangle d'or
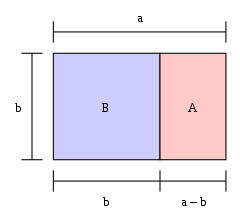
Si la longueur d'un rectangle divisée par sa largeur est égale au nombre d'or, alors le rectangle est un "rectangle d'or". Si un carré est coupé à une extrémité d'un rectangle doré, alors l'autre extrémité est un nouveau rectangle doré. Sur l'image, le grand rectangle (bleu et rose ensemble) est un rectangle d'or parce que a / b = φ {\displaystyle a/b=\varphi }
. La partie bleue (B) est un carré. La partie rose en elle-même (A) est un autre rectangle doré car b / ( a - b ) = φ {\displaystyle b/(a-b)=\varphi }
. Le grand rectangle et le rectangle rose ont la même forme, mais le rectangle rose est plus petit et est tourné.
Le grand rectangle BA est un rectangle doré ; c'est-à-dire que la proportion b:a est de 1 : φ {\displaystyle \varphi } . Pour un tel rectangle, et seulement pour les rectangles de cette proportion spécifique, si nous enlevons le carré B, ce qui reste, A, est un autre rectangle doré, c'est-à-dire avec les mêmes proportions que le rectangle original.
Les chiffres de Fibonacci
Les numéros de Fibonacci sont une liste de numéros. Une personne peut trouver le numéro suivant dans la liste en additionnant les deux derniers numéros. Si une personne divise un nombre de la liste par le nombre qui l'a précédé, ce rapport se rapproche de plus en plus du nombre d'or.
| Numéro de Fibonacci | divisé par celui d'avant | ratio |
| 1 | ||
| 1 | 1/1 | = 1.0000 |
| 2 | 2/1 | = 2.0000 |
| 3 | 3/2 | = 1.5000 |
| 5 | 5/3 | = 1.6667 |
| 8 | 8/5 | = 1.6000 |
| 13 | 13/8 | = 1.6250 |
| 21 | 21/13 | = 1.6154... |
| 34 | 34/21 | = 1.6190... |
| 55 | 55/34 | = 1.6177... |
| 89 | 89/55 | = 1.6182... |
| ... | ... | ... |
| φ {\displaystyle \varphi } | = 1.6180... |
Le nombre d'or dans la nature
Dans la nature, le nombre d'or est souvent utilisé pour l'arrangement des feuilles ou des fleurs. Celles-ci utilisent l'angle d'or d'environ 137,5 degrés. Les feuilles ou les fleurs disposées selon cet angle utilisent au mieux la lumière du soleil.
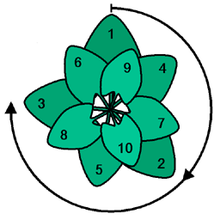
L'utilisation de l'angle d'or permettra d'utiliser de manière optimale la lumière du soleil. Voici une vue d'en haut.
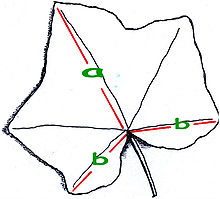
Une feuille de lierre commun, montrant la proportion dorée
Questions et réponses
Q : Quel est le rapport de deux nombres ?
R : On trouve le rapport de deux nombres en les divisant, le rapport serait donc a/b.
Q : Comment peut-on trouver un autre rapport ?
R : On peut trouver un autre rapport en additionnant les deux nombres, puis en divisant cette somme par le plus grand nombre, a. Ce nouveau rapport serait (a+b)/a.
Q : Comment appelle-t-on le moment où ces deux rapports sont égaux l'un à l'autre ?
R : Lorsque ces deux rapports sont égaux l'un à l'autre, on l'appelle le nombre d'or. Il est généralement représenté par la lettre grecque צ ou phi.
Q : Si b = 1 et a/b = צ , qu'est-ce que cela signifie pour a ?
R : Si b = 1 et a/b = צ , cela signifie que a = צ également.
Q : Comment peut-on écrire ce nombre d'une certaine façon ?
R : Une façon d'écrire ce nombre est צ = 1 + 5 / 2 = 1,618...
Q : Que signifie le fait de soustraire 1 de ce nombre ou de le diviser par 1 ?
R : Si vous soustrayez 1 de ce nombre ou divisez 1 par ce nombre, vous retrouverez le même nombre - en d'autres termes, ils seront tous deux égaux au nombre d'or.
Q : Le nombre d'or est-il un nombre irrationnel ?
R : Oui, le nombre d'or est un nombre irrationnel, ce qui signifie que si quelqu'un essaie de l'écrire, il n'y aura jamais de fin ni de modèle - il faut commencer par quelque chose comme "1,6180339887...".
