Fonction (mathématiques)
En mathématiques, une fonction est un objet mathématique qui produit une sortie, lorsqu'on lui donne une entrée - il peut s'agir d'un nombre, d'un vecteur ou de tout ce qui peut exister à l'intérieur d'un ensemble de choses.
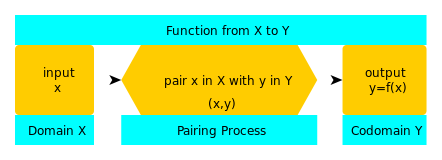
Une fonction est donc comme une machine, qui prend des valeurs de x et renvoie une sortie y. L'ensemble de toutes les valeurs que x peut avoir est appelé le domaine. L'ensemble qui contient toutes les valeurs que y peut avoir est appelé le codomaine.
Si cela se produit, on dit que y est une fonction de x, et on écrit y =f(x). f est le nom de la fonction et on écrit f : X → Y {\displaystyle f:X\to Y}
(fonction de X à Y) pour représenter les trois parties de la fonction : le domaine (x), le codomaine (y) et le processus d'appariement (la flèche).
Un exemple de fonction est f(x)=x+1 On donne un nombre naturel x {\style d'affichage x}
(0,1,2,3...) comme entrée et on obtient un nombre naturel y {\style d'affichage y}
L'idée d'une fonction a été mise en place pour couvrir toutes sortes de possibilités. La fonction n'a pas besoin d'être une équation. L'idée principale est que les entrées et les sorties sont appariées d'une manière ou d'une autre, même si le processus est très compliqué.
Questions et réponses
Q : Qu'est-ce qu'une fonction en mathématiques ?
R : Une fonction en mathématiques est un objet qui produit une sortie lorsqu'on lui donne une entrée, qui peut être un nombre, un vecteur ou tout ce qui peut exister dans un ensemble de choses.
Q : Quels sont les deux ensembles associés aux fonctions ?
R : L'ensemble de toutes les valeurs que x peut avoir est appelé le domaine et l'ensemble qui contient toutes les valeurs que y peut avoir est appelé le codomaine.
Q : Comment les fonctions sont-elles souvent désignées ?
R : Les fonctions sont souvent dénotées par des lettres italiques telles que f, g, h.
Q : Comment représentons-nous une fonction ?
R : Nous représentons une fonction en écrivant y = f(x), où f est le nom de la fonction et on écrit f : X → Y (fonction de X à Y) pour représenter les trois parties de la fonction - domaine (X), codomaine (Y) et processus d'appariement (la flèche).
Q : Pouvez-vous donner un exemple d'une fonction ?
R : Un exemple de fonction est f(x) = x + 1. On donne un nombre naturel x en entrée et on obtient un nombre naturel y qui est x + 1. Par exemple, en donnant 3 en entrée à f, on obtient 4 en sortie.
Q : Chaque fonction doit-elle être une équation ?
R : Non, toutes les fonctions n'ont pas besoin d'être une équation. L'idée principale des fonctions est que les entrées et les sorties sont associées d'une manière ou d'une autre, même si cela peut être très compliqué.
