Distribution statistique
En statistique, une distribution de fréquence est une liste des valeurs qu'une variable prend dans un échantillon. Il s'agit généralement d'une liste, classée par quantité. Elle indique le nombre de fois que chaque valeur apparaît. Par exemple, si 100 personnes évaluent sur une échelle de Likert à cinq points leur accord avec une déclaration sur une échelle où 1 indique un fort accord et 5 un fort désaccord, la distribution de fréquence de leurs réponses pourrait ressembler à ceci :
Ce tableau simple présente deux inconvénients. Lorsqu'une variable peut prendre des valeurs continues au lieu de valeurs discrètes ou lorsque le nombre de valeurs possibles est trop important, la construction du tableau est difficile, voire impossible. Un schéma légèrement différent basé sur la plage de valeurs est utilisé dans de tels cas. Par exemple, si l'on considère la taille des élèves d'une classe, le tableau des fréquences pourrait ressembler à celui ci-dessous.
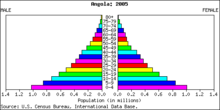
Exemple d'une distribution de fréquences (absolue). Voici la pyramide de la population de l'Angola, pour l'année 2005.

Il s'agit de la pyramide des âges de la Chine pour l'année 2005.
Demandes
La gestion et l'exploitation des données tabulées par fréquence est beaucoup plus simple que l'exploitation des données brutes. Il existe des algorithmes simples pour calculer la médiane, la moyenne (statistiques), l'écart-type, etc. à partir de ces tableaux.
La vérification des hypothèses statistiques est basée sur l'évaluation des différences et des similitudes entre les distributions de fréquences. Cette évaluation comprend des mesures de la tendance centrale ou des moyennes, comme la moyenne et la médiane, et des mesures de la variabilité ou de la dispersion statistique, comme l'écart type ou la variance.
On dit qu'une distribution de fréquences est faussée lorsque sa moyenne et sa médiane sont différentes. L'aplatissement d'une distribution de fréquences est la concentration des scores à la moyenne, ou la façon dont la distribution apparaît en pointe si elle est représentée graphiquement, par exemple dans un histogramme. Si la distribution est plus pointue que la distribution normale, on dit qu'elle est leptokurtique ; si elle est moins pointue, on dit qu'elle est platykurtique.
Les distributions de fréquences sont également utilisées dans l'analyse des fréquences pour craquer les codes et se référer à la fréquence relative des lettres dans les différentes langues.
Questions et réponses
Q : Qu'est-ce qu'une distribution de fréquences ?
R : Une distribution de fréquences est une liste des valeurs que prend une variable dans un échantillon, classées par quantité. Elle montre combien de fois chaque valeur apparaît.
Q : À quoi peut ressembler la distribution de fréquence des réponses à une échelle de Likert à cinq points ?
R : La distribution de fréquence des réponses à une échelle de Likert à cinq points pourrait ressembler à un simple tableau montrant le nombre de personnes ayant évalué chaque point de l'échelle.
Q : Quels sont les deux inconvénients de l'utilisation de ce type de tableau ?
R : Deux inconvénients à l'utilisation de ce type de tableau sont qu'il peut être difficile, voire impossible, de traiter des valeurs continues ou lorsqu'il y a trop de valeurs possibles.
Q : En quoi ce schéma est-il différent lorsqu'on traite des valeurs continues ou un grand nombre de valeurs possibles ?
R : Lorsqu'il s'agit de valeurs continues ou d'un grand nombre de valeurs possibles, un schéma légèrement différent basé sur la plage de valeurs peut être utilisé à la place.
Q : À quoi peut ressembler le tableau de fréquence des tailles des élèves ?
R : Le tableau de fréquence pour les hauteurs des élèves peut montrer des plages et le nombre d'élèves qui se trouvent dans chaque plage.
Q : Quelles informations la distribution de fréquences fournit-elle ?
R : La distribution de fréquence fournit des informations sur la fréquence d'apparition de certaines variables dans les échantillons et sur leur répartition dans ces échantillons.
Rechercher dans l'encyclopédie