Fractale
Une fractale est un motif qui, lorsqu'il est vu comme une image, produit une image qui, lorsqu'elle est zoomée, produit toujours la même image. Elle peut être découpée en parties qui ressemblent à une version plus petite de l'image de départ. Le mot fractal a été créé par Benoît Mandelbrot en 1975 à partir du mot latin fractus, qui signifie "cassé" ou "fracturé". Un exemple simple est un arbre qui se ramifie en petites branches, et ces branches en petites branches et ainsi de suite. Les fractales ne sont pas seulement belles, mais elles ont aussi de nombreuses applications pratiques.
Un triangle de Sierpinski, après 7 itérations.
L'ensemble de Mandelbrot est un exemple célèbre de fractale.
Exemples
Il existe de nombreux types de fractales, fabriquées de manières très diverses. Un exemple est le triangle de Sierpinski, où il y a un nombre infini de petits triangles à l'intérieur du grand triangle. Un autre exemple est l'ensemble de Mandelbrot, nommé d'après Benoît Mandelbrot. Le triangle de Sierpinksi est construit à l'aide de motifs, mais l'ensemble de Mandelbrot est basé sur une équation.
Il existe également de nombreux exemples naturels de fractales dans la nature, notamment les arbres, les flocons de neige, certains légumes et les côtes.
La courbe de Koch
La courbe de Koch est un exemple simple de fractale. Commencez d'abord par une partie d'une ligne droite - appelée segment de ligne droite. Coupez la ligne en trois morceaux de même taille. Débarrassez-vous du milieu de ces morceaux et placez la partie supérieure d'un triangle dont les côtés sont de la même longueur que le morceau à découper. Nous avons maintenant 4 segments de ligne qui se touchent aux extrémités. Nous pouvons maintenant faire ce que nous venons de faire au premier segment pour chacun des 4 morceaux. Nous pouvons maintenant faire la même chose, encore et encore, à tous les bits qui se trouvent aux extrémités. Nous pouvons maintenant le faire pour toujours et regarder ce que nous obtenons.
La longueur de la courbe de Koch est infinie, et la surface de la courbe de Koch est nulle. C'est assez étrange. Un segment de ligne (de dimension 1) pourrait avoir une longueur de 1, mais son aire est de 0. Un carré de longueur 1 et de largeur 1 (de dimension 2) aura une aire 1 et une longueur infinie.
La dimension de la similitude
Ainsi, la courbe de Koch semble être plus grande que quelque chose de dimension 1, et plus petite que quelque chose de dimension 2. L'idée de la dimension de similitude est de donner une dimension qui donne une meilleure idée de la longueur ou de la surface des fractales. Ainsi, pour une courbe de Koch, nous voulons une dimension comprise entre 1 et 2.
La courbe de Koch peut être découpée en quatre morceaux, chacun d'entre eux ayant
une taille égale à celle de l'original. Nous appelons le nombre de morceaux qu'une fractale peut être coupée en N,
et nous appelons la différence de taille B
. Nous les mettons dans l'équation :
log N - log B {\displaystyle {\frac {\log N}{-\log B}}}
Où log est
le logarithme d'un nombre. Ce nombre est la dimension de Hausdorff de la fractale. Dans la courbe de Koch, il s'agit du log 4 - log 1 3 = 1,2619... {\displaystyle {\frac 4}{-\log {\frac {1}{3}}}}=1.2619... }
comme nous le voulions.
La courbe de Koch est l'une des formes fractales les plus simples, et sa dimension est donc facile à calculer. Sa dimension de similitude et sa dimension de Hausdorff sont toutes deux identiques. Cela n'est pas vrai pour les fractales plus complexes.
Le flocon de neige de Koch
Le flocon de neige de Koch (ou étoile de Koch) est identique à la courbe de Koch, sauf qu'il commence par un triangle équilatéral au lieu d'un segment de droite.
Comment faire la courbe de Koch
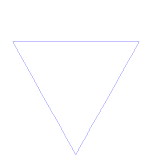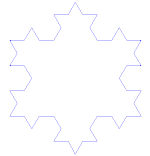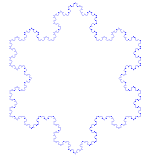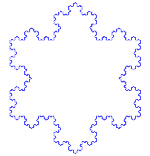
Utilise
Les fractales ont de nombreuses applications, par exemple en biologie (poumons, reins, variabilité du rythme cardiaque, etc.), en cas de tremblement de terre, en finance où elles sont liées aux distributions de la queue dite lourde et en physique. Cela indique qu'il faut étudier les fractales pour comprendre pourquoi elles sont si fréquentes dans la nature.
Certaines fractales n'existent que pour des raisons artistiques, mais d'autres sont très utiles. Les fractales sont des formes très efficaces pour les antennes radio et sont utilisées dans les puces informatiques pour relier efficacement tous les composants. On peut également considérer les côtes comme des fractales.
Questions et réponses
Q : Qu'est-ce qu'une fractale ?
R : Une fractale est un motif qui, vu comme une image, produit une image qui reste la même lorsqu'on l'agrandit.
Q : Qui a inventé le terme "fractale" ?
R : C'est Benoît Mandelbrot qui a inventé le terme "fractale" en 1975.
Q : Quelle est l'étymologie du mot "fractale" ?
R : Le mot "fractale" est dérivé du mot latin "fractus" qui signifie "cassé" ou "fracturé".
Q : Les fractales peuvent-elles être découpées en parties ?
R : Oui, les fractales peuvent être découpées en parties qui ressemblent à une version plus petite de l'image de départ.
Q : Pouvez-vous donner un exemple de fractale ?
R : Un exemple simple de fractale est un arbre qui se ramifie en branches plus petites, et celles-ci en branches plus petites, et ainsi de suite.
Q : Quelles sont les applications pratiques des fractales ?
R : Les fractales ont de nombreuses applications pratiques, notamment dans les domaines de l'infographie, de la médecine, de la physique et de la finance.
Q : Pourquoi les fractales sont-elles importantes ?
R : Les fractales sont importantes parce qu'elles peuvent nous aider à comprendre des phénomènes naturels complexes et à créer des modèles et des simulations plus précis.
