Transformation de Fourier
La transformée de Fourier est une fonction mathématique qui peut être utilisée pour trouver les fréquences de base qui composent un signal ou une onde. Par exemple, si un accord est joué, l'onde sonore de l'accord peut être introduite dans une transformée de Fourier pour trouver les notes qui composent l'accord. La sortie d'une transformée de Fourier est parfois appelée spectre de fréquences ou distribution parce qu'elle affiche un spectre des fréquences de l'entrée. Cette fonction a de nombreuses utilisations en cryptographie, océanographie, apprentissage machine, radiologie, physique quantique ainsi qu'en conception sonore et visualisation.
La transformée de Fourier d'une fonction f(x)
est donnée par
F ( α ) = ∫ - ∞ + ∞ f ( x ) e - 2 π i α x d x {\displaystyle F(\alpha )=\int _{-\infty }^{+\infty }f(x)e^{-2\pi i\alpha x}dx}
α {\displaystyle \alpha }
est une fréquence
F ( α ) {\displaystyle F(\alpha )}
est la fonction de transformée de Fourier et renvoie une valeur représentant la fréquence prévalente α {\displaystyle \alpha } dans le signal original.
e - 2 π i α x {\displaystyle e^{-2\pi i\alpha x}}
Représente l'enroulement de la fonction d'entrée f ( x ) {\displaystyle f(x)} autour de l'origine dans le plan complexe à une certaine fréquence α {\displaystyle \alpha }
La transformée de Fourier inverse est donnée par
f ( x ) = ∫ - ∞ + ∞ F ( α ) e + 2 π i x α d α {\displaystyle f(x)=\int _{-\infty }^{+\infty }F(\alpha )e^{+2\pi ix\alpha }d\alpha }
Une transformée de Fourier montre quelles sont les fréquences dans un signal. Par exemple, considérons une onde sonore qui contient trois notes de musique différentes : A, B, et C. En faisant un graphique de la transformée de Fourier de cette onde sonore (avec la fréquence sur l'axe des x et l'intensité sur l'axe des y), on obtiendra un pic à chaque fréquence qui correspond à l'une des notes de musique.
De nombreux signaux peuvent être créés en additionnant des cosinus et des sinus d'amplitudes et de fréquences variables. La transformée de Fourier trace les amplitudes et les phases de ces cosinus et sinus par rapport à leurs fréquences respectives.
Les transformées de Fourier sont importantes car de nombreux signaux ont plus de sens lorsque leurs fréquences sont séparées. Dans l'exemple audio ci-dessus, si l'on considère le signal par rapport au temps, il n'est pas évident que les notes A, B et C soient dans le signal. De nombreux systèmes font des choses différentes à des fréquences différentes, donc ces types de systèmes peuvent être décrits par ce qu'ils font à chaque fréquence. Un exemple de cela est un filtre qui bloque les hautes fréquences.
Pour calculer une transformée de Fourier, il faut comprendre l'intégration et les nombres imaginaires. Les ordinateurs sont généralement utilisés pour calculer les transformées de Fourier de tout, sauf des signaux les plus simples. La transformée de Fourier rapide est une méthode que les ordinateurs utilisent pour calculer rapidement une transformée de Fourier.
· 
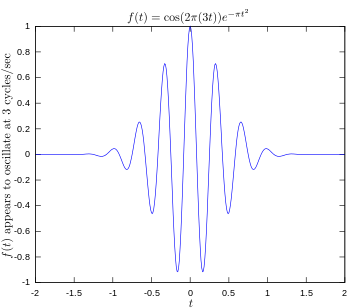
Fonction originale montrant un signal oscillant à 3 hertz.
· 
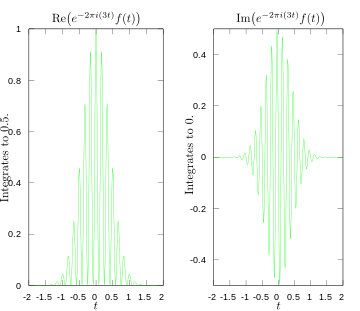
Parties réelles et imaginaires de l'intégrande pour la transformée de Fourier à 3 hertz
· 
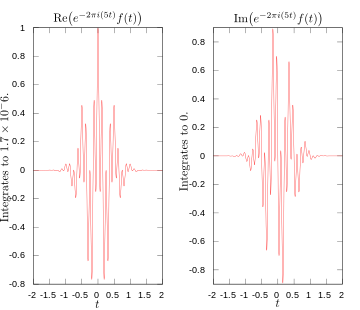
Parties réelles et imaginaires de l'intégrande pour la transformée de Fourier à 5 hertz
· 
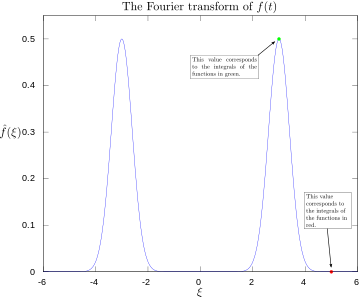
Transformation de Fourier avec 3 et 5 hertz étiquetés.
Questions et réponses
Q : Qu'est-ce que la transformée de Fourier ?
R : La transformée de Fourier est une fonction mathématique qui peut être utilisée pour trouver les fréquences de base dont est composée une onde. Elle prend une onde complexe et trouve les fréquences qui la composent, ce qui lui permet d'identifier les notes qui composent un accord.
Q : Quelles sont les utilisations de la transformée de Fourier ?
R : La transformée de Fourier a de nombreuses utilisations en cryptographie, en océanographie, en apprentissage automatique, en radiologie, en physique quantique ainsi qu'en conception et en visualisation du son.
Q : Comment calcule-t-on la transformée de Fourier ?
R : La transformée de Fourier d'une fonction f(x) est donnée par F(ב) = ∫-∞+∞f(x)e-2נiבxdx où ב est une fréquence. Cela renvoie une valeur représentant la prévalence de la fréquence ב dans le signal original. La transformée de Fourier inverse est donnée par f(x) = ∫-∞+∞F(ב)e+2נixבdב.
Q : A quoi ressemble la sortie d'une transformée de Fourier ?
R : La sortie d'une transformée de Fourier peut être appelée spectre ou distribution de fréquences car elle affiche une distribution des fréquences possibles de l'entrée.
Q : Comment les ordinateurs calculent-ils les transformées de Fourier rapides ?
R : Les ordinateurs utilisent un algorithme appelé transformée de Fourier rapide (FFT) pour calculer rapidement toutes les transformées des signaux, sauf les plus simples.
Q : Que ne nous montre pas l'observation des signaux par rapport au temps ?
R : Regarder des signaux par rapport au temps ne permet pas de savoir quelles notes sont présentes dans ces signaux. De nombreux signaux ont plus de sens lorsque leurs fréquences sont séparées et analysées individuellement à la place.
