Théorème des quatre couleurs

Formulation exacte du problème

Intuitivement, le théorème des quatre couleurs peut être énoncé comme suit : "étant donné toute séparation d'un plan en régions contiguës, appelée carte, les régions peuvent être colorées en utilisant au maximum quatre couleurs de sorte qu'aucune région adjacente n'ait la même couleur". Pour pouvoir résoudre correctement le problème, il est nécessaire de clarifier certains aspects : Premièrement, tous les points qui appartiennent à trois pays ou plus doivent être ignorés. Deuxièmement, les cartes bizarres avec des régions de superficie finie et de périmètre infini peuvent nécessiter plus de quatre couleurs.

Pour les besoins du théorème, chaque "pays" doit être une région simplement connectée, ou contiguë. Dans le monde réel, ce n'est pas vrai : L'Alaska, qui fait partie des États-Unis, le Nakhitchevan, qui fait partie de l'Azerbaïdjan, et Kaliningrad, qui fait partie de la Russie, ne sont pas contigus. Comme le territoire d'un pays donné doit être de la même couleur, quatre couleurs peuvent ne pas suffire. Considérez par exemple une carte simplifiée, telle que celle présentée à gauche : Sur cette carte, les deux régions marquées A appartiennent au même pays et doivent être de la même couleur. Cette carte nécessite alors cinq couleurs, puisque les deux régions A ensemble sont contiguës à quatre autres régions, dont chacune est contiguë à toutes les autres. Si A n'avait que trois régions, six couleurs ou plus pourraient être nécessaires. De cette façon, il est possible de faire des cartes qui nécessitent un nombre arbitrairement élevé de couleurs. Une construction similaire s'applique également si une seule couleur est utilisée pour toutes les masses d'eau, comme c'est habituellement le cas sur les cartes réelles.

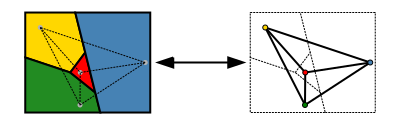
Une version plus facile à énoncer du théorème utilise la théorie des graphes. L'ensemble des régions d'une carte peut être représenté de manière plus abstraite sous la forme d'un graphe non orienté qui possède un sommet pour chaque région et un bord pour chaque paire de régions qui partagent un segment de frontière. Ce graphe est plan : il peut être dessiné dans le plan sans croisement en plaçant chaque sommet à un endroit arbitrairement choisi dans la région à laquelle il correspond, et en dessinant les bords comme des courbes qui mènent sans croisement dans chaque région de l'endroit du sommet à chaque point limite partagé de la région. Inversement, tout graphique planaire peut être formé de cette manière à partir d'une carte. Dans la terminologie de la théorie des graphes, le théorème des quatre couleurs stipule que les sommets de chaque graphe planaire peuvent être colorés avec au maximum quatre couleurs de sorte qu'aucun sommet adjacent n'ait la même couleur, ou en bref, "chaque graphe planaire est quadrichromique" (Thomas 1998, p. 849 ; Wilson 2002).

Exemple de carte de l'Azerbaïdjan avec des régions non contiguës


Cette carte ne peut pas être colorée avec quatre couleurs

Histoire

La première personne à nommer le problème a été Francis Guthrie, en 1852. Il était alors étudiant en droit en Angleterre. Il a découvert qu'il avait besoin d'au moins quatre couleurs pour colorier une carte des comtés d'Angleterre. Augustus de Morgan a abordé le problème pour la première fois dans une lettre qu'il a écrite à Rowan Hamliton en août 1852. Dans cette lettre, de Morgan demande si quatre couleurs sont vraiment suffisantes pour colorier une carte, de sorte que les pays qui sont à côté les uns des autres obtiennent des couleurs différentes.

Le mathématicien anglais Arthur Cayley a présenté le problème à la société mathématique de Londres, en 1878. En un an, Alfred Kempe a trouvé ce qui semblait être une preuve du problème. Onze ans plus tard, en 1890, Percy Heawood a montré que la preuve d'Alfred était fausse. Peter Guthrie Tait a présenté une autre tentative de preuve en 1880. Il a fallu onze ans pour montrer que la preuve de Tait ne fonctionnait pas non plus. En 1891, Julius Petersen a pu le démontrer. Lorsqu'il a falsifié la preuve de Cayley, Kempe a également montré une preuve pour un problème qu'il a appelé le théorème des cinq couleurs. Le théorème dit que toute carte de ce type ne peut être colorée avec plus de cinq couleurs. Il y a deux restrictions : Premièrement, tout pays est contigu, il n'y a pas d'exclaves. La seconde restriction est que les pays doivent avoir une frontière commune ; s'ils ne se touchent qu'en un point, ils peuvent être coloriés avec la même couleur. Même si la preuve de Kempe était fausse, il a utilisé certaines des idées qui permettraient plus tard une preuve correcte.

Dans les années 1960 et 1970, Heinrich Heesch a développé une première ébauche de preuve par ordinateur. Kenneth Appel et Wolfgang Haken ont amélioré cette esquisse en 1976 (Robertson et al. 1996). Ils ont réussi à réduire le nombre de cas à tester à 1936 ; une version ultérieure a été réalisée en ne testant que 1476 cas. Chaque cas devait être testé par un ordinateur (Appel & Haken 1977).

En 1996, Neil Robertson, Daniel Sanders, Paul Seymour et Robin Thomas ont amélioré la méthode et réduit le nombre de cas à tester à 663. Là encore, chaque cas devait être testé par ordinateur.

En 2005, Georges Gonthier et Benjamin Werner ont élaboré une preuve formelle. Il s'agissait d'une amélioration, car elle permettait d'utiliser pour la première fois un logiciel de démonstration de théorèmes. Le logiciel utilisé s'appelle Coq.

Le théorème des quatre couleurs est le premier grand problème mathématique qui a été prouvé à l'aide d'un ordinateur. Comme la preuve ne peut pas être faite par un humain, certains mathématiciens ne l'ont pas reconnue comme correcte. Pour vérifier la preuve, il est nécessaire de s'appuyer sur un logiciel et un matériel qui fonctionnent correctement pour valider la preuve. Comme la preuve a été faite par ordinateur, elle n'est pas non plus très élégante.

Des tentatives qui se sont révélées fausses

Le théorème des quatre couleurs est connu pour avoir attiré un grand nombre de fausses preuves et de réfutations au cours de sa longue histoire. Au début, le New York Times a refusé de faire un reportage sur la preuve d'Appel-Haken. Le journal l'a fait par principe ; il craignait que la preuve soit présentée comme fausse, comme celles qui l'avaient précédée (Wilson 2002, p. 209). Certaines preuves ont pris beaucoup de temps avant d'être falsifiées : Pour les preuves de Kempe et Tait, il a fallu plus d'une décennie pour les falsifier.

Les contre-exemples les plus simples tentent généralement de créer une région qui touche toutes les autres. Cela oblige à colorer les régions restantes avec seulement trois couleurs. Comme le théorème des quatre couleurs est vrai, cela est toujours possible ; cependant, comme la personne qui dessine la carte est concentrée sur la seule grande région, elle ne remarque pas que les régions restantes peuvent en fait être colorées avec trois couleurs.

Cette astuce peut être généralisée : Si les couleurs de certaines régions d'une carte sont choisies à l'avance, il devient impossible de colorer les régions restantes de telle sorte qu'au total, seules quatre couleurs sont utilisées. Une personne qui vérifie le contre-exemple peut penser qu'il n'est pas nécessaire de changer la couleur de ces régions. Le contre-exemple paraîtra alors valable, même s'il ne l'est pas.

Un des effets sous-jacents de cette idée fausse est peut-être le fait que la restriction des couleurs n'est pas transitive : une région doit seulement être colorée différemment des régions qu'elle touche directement, et non les régions qui touchent les régions qu'elle touche. Si c'était le cas, les graphiques planaires nécessiteraient un nombre arbitrairement élevé de couleurs.

D'autres fausses preuves violent les hypothèses du théorème de manière inattendue, comme l'utilisation d'une région qui a de multiples parties déconnectées, ou le fait de ne pas permettre à des régions de même couleur de se toucher en un point.

Coloriage des cartes politiques

Dans la vie réelle, de nombreux pays ont des exclaves ou des colonies. Comme ils appartiennent au pays, ils doivent être colorés de la même couleur que le pays d'origine. Cela signifie qu'en général, plus de quatre couleurs sont nécessaires pour colorier une telle carte. Lorsque les mathématiciens parlent du graphique associé au problème, ils disent qu'il n'est pas plan. Même s'il est facile de vérifier si un graphique est plan, il est très difficile de trouver le plus petit nombre de couleurs nécessaires pour le colorier. Il est NP-complet, ce qui est l'un des problèmes les plus difficiles qui existent. Le plus petit nombre de couleurs nécessaires pour colorier un graphique est connu sous le nom de nombre chromatique. Beaucoup de problèmes qui se posent lorsqu'on essaie de résoudre le théorème des quatre couleurs sont liés aux mathématiques discrètes. Pour cette raison, des méthodes de topologie algébrique sont souvent utilisées.

Extension aux cartes "non planes

Le théorème des quatre couleurs exige que la "carte" se trouve sur une surface plane, ce que les mathématiciens appellent un plan. En 1890, Percy John Heawood a créé ce que l'on appelle aujourd'hui la conjecture de Heawood : Elle pose la même question que le théorème des quatre couleurs, mais pour tout objet topologique. Par exemple, un tore peut être coloré avec sept couleurs au maximum. La conjecture de Heawood donne une formule qui fonctionne pour tous ces objets, à l'exception de la bouteille de Klein.