Fonction exponentielle
En mathématiques, une fonction exponentielle est une fonction qui croît rapidement. Plus précisément, il s'agit de la fonction exp ( x ) = e x {\displaystyle \exp(x)=e^{x}}
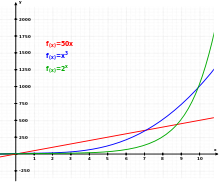
Trois fonctions différentes : Linéaire (rouge), Cubique (bleu) et Exponentiel (vert).
Propriétés
Comme les fonctions exponentielles utilisent l'exponentiation, elles suivent les mêmes règles. Ainsi, les fonctions exponentielles
exp ( x + y ) = exp ( x ) exp ( y ) = e x + y {\displaystyle \exp(x+y)=\exp(x)\exp(y)=e^{x+y}}

Le logarithme naturel est l'opération inverse d'une fonction exponentielle.
ln ( x ) = log e ( x ) = log ( x ) log ( e ) {\displaystyle \ln(x)=\log _{e}(x)={\frac {\log(x)}{\log(e)}}}
La fonction exponentielle satisfait une propriété intéressante et importante dans le calcul différentiel,
d d x e x = e x }{\mathrm {d} x}}}e^{x}=e^{x}}
Cela signifie que la pente de la fonction exponentielle est la fonction exponentielle elle-même, ce qui signifie qu'elle a une pente de 1 à x = 0 {\style d'affichage x=0}
Demandes
La fonction exponentielle est l'une des plus utiles des fonctions mathématiques. Elle est utilisée pour représenter la croissance exponentielle, qui a des utilisations dans pratiquement toutes les matières scientifiques et elle est également importante en finance. La décroissance exponentielle se produit également, par exemple la décroissance radioactive et l'absorption de la lumière.
Un exemple de fonction exponentielle dans la vie réelle serait l'intérêt pour une banque. Si une personne dépose 100 £ sur un compte qui rapporte 3 % d'intérêts par mois, le solde mensuel sera (en supposant que l'argent n'est pas touché) :
| Mois | Balance | Mois | Balance |
| Janvier | £100.00 | Juillet | £119.41 |
| Février | £103.00 | Août | £122.99 |
| Mars | £106.09 | Septembre | £126.68 |
| Avril | £109.27 | Octobre | £130.48 |
| Mai | £112.55 | Novembre | £134.39 |
| Juin | £115.93 | Décembre | £138.42 |
Remarquez comment l'argent supplémentaire provenant des intérêts augmente chaque mois. Plus le solde initial est élevé, plus la personne recevra d'intérêts.
Deux exemples mathématiques de fonctions exponentielles sont présentés ci-dessous.
| a=2
| a=3
|
Relation avec la constante mathématique e
Même si la base (a)
Le nombre e est important pour toute fonction exponentielle. Par exemple, une banque paie des intérêts de 0,01 % chaque jour. Une personne prend l'argent de ses intérêts et le met dans une boîte. Après 10 000 jours (environ 30 ans), il a deux fois plus d'argent qu'au départ. Une autre personne prend l'argent de ses intérêts et le remet à la banque. Comme la banque lui verse désormais des intérêts sur ses intérêts, la somme d'argent est une fonction exponentielle. Après 10 000 jours, il n'a pas deux fois plus d'argent qu'au départ, mais il en a 2,718145 fois plus qu'au départ. Ce chiffre est très proche du chiffre e. Si la banque paie des intérêts plus souvent, donc que le montant payé à chaque fois est inférieur, alors le chiffre sera plus proche du chiffre e.
Une personne peut également regarder l'image pour voir pourquoi le nombre e est important pour les fonctions exponentielles. L'image présente trois courbes différentes. La courbe avec les points noirs est une fonction exponentielle avec une base un peu plus petite que e. La courbe avec les lignes noires courtes est une fonction exponentielle avec une base un peu plus grande que e. La courbe bleue est une fonction exponentielle avec une base exactement égale à e. La ligne rouge est une tangente à la courbe bleue. Elle touche la courbe bleue en un point sans la croiser. Une personne peut voir que la courbe rouge croise l'axe des x, la ligne qui va de gauche à droite, à -1. Cela n'est vrai que pour la courbe bleue. C'est la raison pour laquelle la fonction exponentielle avec la base e est spéciale.
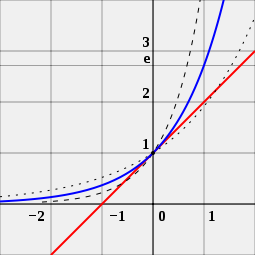
e est le nombre unique a, tel que la valeur de la dérivée de la fonction exponentielle f (x) = ax (courbe bleue) au point x = 0 est exactement 1. À titre de comparaison, les fonctions 2x (courbe en pointillés) et 4x (courbe en tirets) sont présentées ; elles ne sont pas tangentes à la ligne de la pente 1 (rouge).
Questions et réponses
Q : Qu'est-ce que la fonction exponentielle ?
R : La fonction exponentielle est une fonction mathématique qui croît de plus en plus vite.
Q : Comment la fonction exponentielle est-elle exprimée mathématiquement ?
R : La fonction exponentielle s'exprime mathématiquement par exp(x) = e^x, où e est la constante d'Euler.
Q : Que représente la constante d'Euler ?
R : La constante d'Euler représente un nombre irrationnel qui vaut approximativement 2,71828.
Q : La fonction exponentielle est-elle toujours croissante ?
R : Oui, la fonction exponentielle augmente toujours en valeur lorsque x augmente.
Q : Existe-t-il une limite à la vitesse de croissance de la fonction exponentielle ?
R : Non, il n'y a pas de limite à la vitesse à laquelle la fonction exponentielle peut croître puisqu'elle continue à augmenter avec des valeurs plus grandes de x.
Q : Comment pouvons-nous calculer la constante d'Euler ?
R : Nous pouvons calculer la constante d'Euler en utilisant des méthodes numériques telles que les séries de Taylor ou les fractions continues.
Q : Quelles sont les autres applications de la fonction exponentielle en dehors des mathématiques ?
R : La fonction exponentielle a de nombreuses applications en dehors des mathématiques, notamment en physique, chimie, biologie, économie et ingénierie.
Rechercher dans l'encyclopédie

