Formule d'Euler
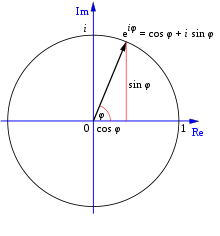
La formule d'Euler, que l'on appelle parfois la relation d'Euler, est une équation d'analyse. Elle établit une relation entre des fonctions trigonométriques et des fonctions exponentielles de nombres complexes. Elle porte le nom de Leonhard Euler, qui l'a publiée en 1748. Lorsqu'il l'a publiée, Euler a dit que l'angle doit être un nombre réel. Plus tard, il s'est avéré que la formule fonctionne également si l'angle n'est pas un nombre réel, mais un nombre complexe.
Questions et réponses
Q : Qu'est-ce que la formule d'Euler ?
R : La formule d'Euler est une équation impliquant des nombres complexes et des fonctions trigonométriques qui relie les fonctions exponentielles des nombres complexes aux fonctions trigonométriques.
Q : Qui a publié la formule d'Euler ?
R : Leonhard Euler a publié la formule d'Euler en 1748.
Q : La formule fonctionne-t-elle lorsque l'angle n'est pas un nombre réel ?
R : Oui, il s'avère que la formule fonctionne également si l'angle est un nombre complexe.
Q : Que se passe-t-il lorsque l'angle est égal à pi ?
R : Lorsque l'angle est pi, la formule d'Euler devient e^iנ = -1.
Q : Que se passe-t-il lorsque l'angle est égal à 2pi ?
R : Lorsque l'angle est 2pi, la formule d'Euler devient e^i2נ = 1.
Q : Que représente "e" dans cette équation ?
R : Dans cette équation, "e" représente le nombre d'Euler.
Q : Que représente "i" dans cette équation ?
R : Dans cette équation, "i" représente l'unité imaginaire.
