Théorie des poutres
La théorie des poutres d'Euler-Bernoulli (également appelée théorie des poutres d'ingénieur ou théorie classique des poutres) est une méthode simple pour calculer la flexion des poutres lorsqu'une charge est appliquée. Elle s'applique aux petites déflexions (la distance à laquelle quelque chose se déplace) d'une poutre sans tenir compte des effets des déformations en cisaillement. Par conséquent, elle peut être considérée comme un cas particulier de la théorie des poutres de Timoshenko. Elle a été introduite pour la première fois vers 1750. Elle a gagné en popularité lors du développement de la tour Eiffel et de la grande roue à la fin du 19e siècle. Par la suite, elle a été utilisée dans de nombreux domaines de l'ingénierie, notamment le génie mécanique et le génie civil. Bien que d'autres méthodes avancées aient été développées, la théorie du faisceau d'Euler-Bernoulli est encore largement utilisée en raison de sa simplicité.
Une poutre de verre vibrante montrant la flexion des poutres qui peut être estimée à l'aide de la théorie des poutres d'Euler-Bernoulli.
Histoire
Leonhard Euler et Daniel Bernoulli ont été les premiers à élaborer cette théorie en 1750. À l'époque, la science et l'ingénierie étaient perçues différemment de celles d'aujourd'hui. Les théories mathématiques telles que la théorie du faisceau Euler-Bernoulli n'étaient pas fiables pour une utilisation pratique en ingénierie. Les ponts et les bâtiments ont continué à être conçus selon les mêmes méthodes jusqu'à la fin du XIXe siècle. C'est alors que la tour Eiffel et la grande roue ont montré la validité de la théorie à une plus grande échelle.
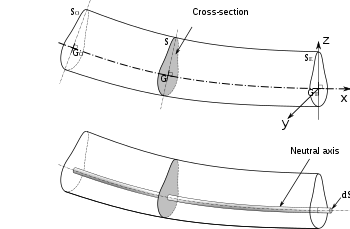
Dessin d'une section transversale d'une poutre courbée montrant l'axe neutre
Équation du faisceau statique
L'équation d'Euler-Bernoulli décrit la relation entre la déflexion de la poutre et la charge appliquée, comme indiqué ci-dessous :
d 2 d x 2 ( E I d 2 w d x 2 ) = q {\displaystyle {\frac {\mathrm {d} ^{2}}{\mathrm {d} x^{2}}}\left(EI{\frac {mathrm {d} ^{2}w}{\mathrm {d} x^{2}}}\right)=q\,}
Où w ( x ) {\displaystyle w(x)}
décrit la déflexion du faisceau dans la
direction z {\displaystyle z} à une certaine position x {\displaystyle x}
. q {\displaystyle q}
est une charge répartie, en d'autres termes une force par unité de longueur (analogue à la pression qui est une force par surface) ; elle peut être une fonction de x {\displaystyle x} , w {\displaystyle w}
ou d'autres variables.
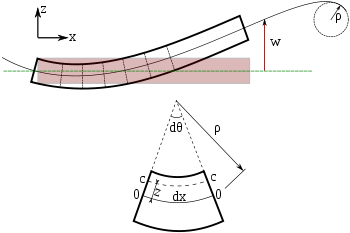
Flexion d'une poutre d'Euler-Bernoulli. Chaque section transversale du faisceau est à 90 degrés par rapport à l'axe neutre.
Questions et réponses
Q : Qu'est-ce que la théorie des poutres d'Euler-Bernoulli ?
R : La théorie des poutres d'Euler-Bernoulli est une méthode simple utilisée pour calculer la flexion des poutres lorsqu'une charge est appliquée, sans tenir compte des effets des déformations de cisaillement.
Q : Quand la théorie des poutres d'Euler-Bernoulli a-t-elle été introduite pour la première fois ?
R : La théorie des poutres d'Euler-Bernoulli a été introduite pour la première fois vers 1750.
Q : La théorie des poutres d'Euler-Bernoulli a-t-elle été utilisée pour la construction de la tour Eiffel et de la grande roue ?
R : Oui, la théorie des poutres d'Euler-Bernoulli a gagné en popularité lors du développement de la tour Eiffel et de la grande roue à la fin du 19e siècle.
Q : Quels sont les domaines de l'ingénierie dans lesquels la théorie des poutres d'Euler-Bernoulli a été utilisée ?
R : La théorie des poutres d'Euler-Bernoulli a été utilisée dans de nombreux domaines de l'ingénierie, notamment le génie mécanique et le génie civil.
Q : La théorie des poutres d'Euler-Bernoulli est-elle encore largement utilisée aujourd'hui ?
R : Oui, la théorie des poutres d'Euler-Bernoulli est encore largement utilisée aujourd'hui en raison de sa simplicité, même si d'autres méthodes avancées ont été développées.
Q : À quels types de déviations d'une poutre la théorie des poutres d'Euler-Bernoulli s'applique-t-elle ?
R : La théorie des poutres d'Euler-Bernoulli s'applique aux petites déviations d'une poutre.
Q : La théorie des poutres d'Euler-Bernoulli prend-elle en compte les effets des déformations de cisaillement ?
R : Non, la théorie des poutres d'Euler-Bernoulli ne prend pas en compte les effets des déformations de cisaillement.
