Ellipse (mathématiques)
Une ellipse est une forme qui ressemble à un ovale ou à un cercle aplati.
En géométrie, une ellipse est une courbe plane qui résulte de l'intersection d'un cône par un plan de manière à produire une courbe fermée.
Les cercles sont des cas particuliers d'ellipses, obtenus lorsque le plan de coupe est perpendiculaire à l'axe du cône. Une ellipse est également le lieu de tous les points du plan dont les distances à deux points fixes s'ajoutent à la même constante.
Un cercle a un centre, appelé foyer, mais une ellipse a deux foyers.
Une ellipse est simplement l'ensemble des points d'un graphique dont la somme des distances de 2 points est la même. Par exemple, on peut faire une ellipse en plaçant deux épingles dans du carton et un cercle de ficelle autour de ces deux épingles, puis en mettant un crayon dans la boucle et en tirant le plus loin possible sans casser la ficelle dans toutes les directions. Les orbites des planètes sont des ellipses, avec le soleil à un foyer et rien à l'autre.
L'équation d'une ellipse est : ( x - h ) 2 a 2 + ( y - k ) 2 b 2 = 1 {\frac {(x-h)^{2}}{a^{2}}}+{\frac {(y-k)^{2}}{b^{2}}}=1}
où le centre de l'ellipse est (h,k). 2A est la longueur à partir de chaque extrémité du côté le plus long et le plus mince. 2b est la longueur des deux extrémités du côté court. A²-B²=C² pour c est la longueur entre les foyers et le centre.

Une ellipse obtenue par l'intersection d'un cône et d'un plan.
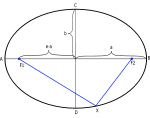
Une ellipse et ses propriétés.
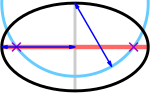
Les foyers (croix violettes) se trouvent aux intersections du grand axe (rouge) et d'un cercle (cyan) de rayon égal au demi-grand axe (bleu), centré sur une extrémité du petit axe (gris)
Questions et réponses
Q : Qu'est-ce qu'une ellipse ?
R : Une ellipse est une forme qui ressemble à un ovale ou à un cercle aplati. En géométrie, c'est une courbe plane qui résulte de l'intersection d'un cône par un plan de manière à produire une courbe fermée.
Q : Comment crée-t-on une ellipse ?
R : On peut créer une ellipse en mettant deux épingles dans du carton, puis en faisant une boucle de ficelle autour de ces deux épingles et en mettant un crayon dans la boucle et en tirant aussi loin que possible sans casser la ficelle dans toutes les directions.
Q : Quels sont les cas particuliers des cercles ?
R : Les cercles sont des cas particuliers d'ellipses, créés lorsque le plan de coupe est perpendiculaire à l'axe du cône.
Q : Combien de foyers une ellipse possède-t-elle ?
R : Une ellipse a deux foyers.
Q : Quelle équation décrit une ellipse ?
R : L'équation d'une ellipse est (x - h)²/a² + (y - k)²/b² = 1 où h et k représentent le centre de l'ellipse et 2a représente la longueur entre chaque extrémité du côté le plus long et le plus court, tandis que 2b représente la longueur entre chaque extrémité de son côté le plus court. C représente la longueur entre son foyer et son centre, de sorte que A²-B²=C².
Q : Où voyons-nous des exemples d'orbites elliptiques ?
R : Les orbites elliptiques peuvent être observées dans les planètes, avec leur soleil à un point focal.
Rechercher dans l'encyclopédie
