Produit scalaire

Définition

Le produit scalaire de deux vecteurs a = [a1, a2, ..., an] et b = [b1, b2, ..., bn] est défini comme suit :

a ⋅ b = ∑ i = 1 n a i b i = a 1 b 1 + a 2 b 2 + ⋯ + a n b n {\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum _{i=1}^{n}a_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+\cdots +a_{n}b_{n}}}

où Σ désigne la notation de sommation ( la somme de tous les termes) et n est la dimension de l'espace vectoriel.

Dans la dimension 2, le produit des points des vecteurs [a,b] et [c,d] est ac + bd. De même, dans une dimension 3, le produit scalaire des vecteurs [a,b,c] et [d,e,f] est ad + be + cf. par exemple, le produit scalaire de deux vecteurs tridimensionnels [1, 3, -5] et [4, -2, -1] est

[ 1 , 3 , − 5 ] ⋅ [ 4 , − 2 , − 1 ] = ( 1 × 4 ) + ( 3 × ( − 2 ) ) + ( ( - 5 ) × ( - 1 ) ) = ( 4 ) - ( 6 ) + ( 5 ) = 3 [style d'affichage [1,3,-5]\cdot [4,-2,-1]=(1\fois 4)+(3\fois (-2))+((-5)\fois (-1))=(4)-(6)+(5)=3.}

Interprétation géométrique

En géométrie euclidienne, le produit des points, la longueur et l'angle sont liés. Pour un vecteur a, le produit scalaire a - a est le carré de la longueur de a, ou

a ⋅ a = ‖ a ‖ 2 {\displaystyle {\mathbf {a} \cdot \mathbf {a} }=\left\|\mathbf {a} \right\|^{2}}

où ||a|| désigne la longueur (magnitude) de a. Plus généralement, si b est un autre vecteur

a ⋅ b = ‖ a ‖ ‖ b ‖ cos θ {\displaystyle \mathbf {a} \cdot \mathbf {b} =\left\|\mathbf {a} \right\|\,\left\|\mathbf {b} \right\|\cos \theta \,}

où ||a|| et ||b|| dénotent la longueur de a et b et θ est l'angle entre eux.

Cette formule peut être réarrangée pour déterminer la taille de l'angle entre deux vecteurs non nuls :

θ = arccos ( a ⋅ b ‖ a ‖ ‖ b ‖ ) {\displaystyle \theta =\arccos \left({\frac {{\mathbf {a}}\cdot {\mathbf {b}}}{\left\|{\mathbf {a}}\right\|\left\|{\mathbf {b}}\right\|}}}\right)}

On peut également commencer par convertir les vecteurs en vecteurs unitaires en les divisant par leur magnitude :

a ^ = a ‖ a ‖ {\displaystyle {\boldsymbol {\hat {a}}}={\frac {\mathbf {a}}{\left\|{\mathbf {a}}\right\|}}}

alors l'angle θ est donné par

θ = arccos ( a ^ ⋅ b ^ ) {\displaystyle \theta =\arccos({\boldsymbol {\hat {a}}}\cdot {\boldsymbol {\hat {b}}})}

Comme le cosinus de 90° est égal à zéro, le produit de deux vecteurs orthogonaux (perpendiculaires) est toujours égal à zéro. En outre, deux vecteurs peuvent être considérés comme orthogonaux si et seulement si leur produit scalaire est nul et s'ils ont tous deux une longueur non nulle. Cette propriété fournit une méthode simple pour tester la condition d'orthogonalité.

Parfois, ces propriétés sont également utilisées pour définir le produit du point, notamment en 2 et 3 dimensions ; cette définition est équivalente à celle ci-dessus. Pour les dimensions supérieures, la formule peut être utilisée pour définir le concept d'angle.

Les propriétés géométriques reposent sur le fait que la base est orthonormée, c'est-à-dire composée de vecteurs perpendiculaires par paires d'unités de longueur.

Projection scalaire

Si a et b ont tous deux la longueur un (c'est-à-dire qu'ils sont des vecteurs unitaires), leur produit scalaire donne simplement le cosinus de l'angle entre eux.

Si seul b est un vecteur unitaire, alors le produit du point a - b donne |a| cos(θ), c'est-à-dire l'amplitude de la projection de a dans la direction de b, avec un signe moins si la direction est opposée. C'est ce qu'on appelle la projection scalaire de a sur b, ou la composante scalaire de a dans la direction de b (voir figure). Cette propriété du produit scalaire a plusieurs applications utiles (par exemple, voir la section suivante).

Si ni a ni b n'est un vecteur unitaire, alors la magnitude de la projection de a dans la direction de b, par exemple, serait a - (b / |b|) car le vecteur unitaire dans la direction de b est b / |b|.

Rotation

Une rotation de la base orthonormée en fonction de laquelle le vecteur a est représenté est obtenue par une multiplication de a par une matrice de rotation R. Cette multiplication matricielle n'est qu'une représentation compacte d'une séquence de produits ponctuels.

Par exemple, laissez

• _B1 = {x, y, z} et B2 = {u, v, w} sont deux bases orthonormales différentes du même espace ^R3, _B2 étant obtenu par simple rotation de _B1,
• a1 = (_ax, _ay, _az) représente le vecteur a en termes de _B1,
• a2 = (_au, _av, _aw) représentent le même vecteur en termes de base de rotation B2,
• u1, v1, w1 sont les vecteurs de base tournante u, v, w représentés en termes de _B1.

Ensuite, la rotation de _B1 à _{B2 s'}effectue comme suit :

a 2 = R a 1 = [ u x u y u z v x v y v z w x w y w z ] [ a x a y a z ] = [ u 1 ⋅ a 1 v 1 ⋅ a 1 w 1 ⋅ a 1 ] = [ a u a v a w ] . {\displaystyle {\mathbf {a}}_{2}={\mathbf {Ra}}_{1}={\begin{bmatrix}u_{x}&u_{y}&u_{z}\\v_{x}&v_{y}&v_{z}\\w_{x}&w_{y}&w_{z}\end{bmatrix}}{\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {v}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}\\a_{v}\\a_{w}\end{bmatrix}}}. }

Notez que la matrice de rotation R est assemblée en utilisant les vecteurs de base tournés u1, v1, w1 comme ses lignes, et ces vecteurs sont des vecteurs unitaires. Par définition, Ra1 est constitué d'une séquence de produits ponctuels entre chacune des trois lignes de R et le vecteur a1. Chacun de ces produits de points détermine une composante scalaire de a dans la direction d'un vecteur de base pivoté (voir la section précédente).

Si a1 est un vecteur ligne, plutôt qu'un vecteur colonne, alors R doit contenir les vecteurs de base tournés dans ses colonnes, et doit post-multiplier a1 :

a 2 = a 1 R = [ a x a y a z ] [ u x v x w x u y v y w y u z v z w z ] = [ u 1 ⋅ a 1 v 1 ⋅ a 1 w 1 ⋅ a 1 ] = [ a u a v a w ] . {\displaystyle {\mathbf {a}}_{2}={\mathbf {a}}_{1}{\mathbf {R}}={\begin{bmatrix}a_{x}&a_{y}&a_{z}\end{bmatrix}}{\begin{bmatrix}u_{x}&v_{x}&w_{x}\\u_{y}&v_{y}&w_{y}\\u_{z}&v_{z}&w_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {v}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}&a_{v}&a_{w}\end{bmatrix}}. }

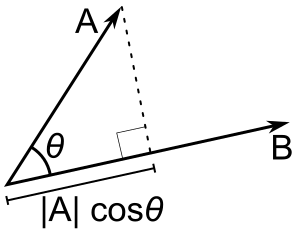
A - B = |A| |B| cos(θ). |A| cos(θ) est la projection scalaire de A sur B.

Physique

En physique, la grandeur est un scalaire au sens physique du terme, c'est-à-dire une quantité physique indépendante du système de coordonnées, exprimée comme le produit d'une valeur numérique et d'une unité physique, et non pas seulement comme un nombre. Le produit du point est également un scalaire dans ce sens, donné par la formule, indépendant du système de coordonnées. Exemple :

• Le travail mécanique est le produit ponctuel de vecteurs de force et de déplacement.
• Le flux magnétique est le produit ponctuel du champ magnétique et des vecteurs de surface.
• Le débit volumétrique est le produit ponctuel de la vitesse du fluide et des vecteurs de surface.

Propriétés

Les propriétés suivantes sont valables si a, b et c sont des vecteurs réels et si r est un scalaire.

Le produit en points est commutatif :

a ⋅ b = b ⋅ a . {\displaystyle \mathbf {a} \cdot \mathbf {b} =\mathbf {b} \cdot \mathbf {a} . }

Le produit des points est distributif par addition vectorielle :

a ⋅ ( b + c ) = a ⋅ b + a ⋅ c . {\displaystyle \mathbf {a} \cdot (\mathbf {b} +\mathbf {c} )=\mathbf {a} \cdot \mathbf {b} +\mathbf {a} \cdot \mathbf {c} . }

Le produit en points est bilinéaire :

a ⋅ ( r b + c ) = r ( a ⋅ b ) + ( a ⋅ c ) . {\displaystyle \mathbf {a} \cdot (r\mathbf {b} +\mathbf {c} )=r(\mathbf {a} \cdot \mathbf {b} )+(\mathbf {a} \cdot \mathbf {c} ). }

Lorsqu'il est multiplié par une valeur scalaire, le produit des points satisfait :

( c 1 a ) ⋅ ( c 2 b ) = ( c 1 c 2 ) ( a ⋅ b ) {\displaystyle (c_{1}\mathbf {a} )\cdot (c_{2}\mathbf {b} )=(c_{1}c_{2})(\mathbf {a} \cdot \mathbf {b} )}

(ces deux dernières propriétés découlent des deux premières).

Deux vecteurs a et b non nuls sont perpendiculaires si et seulement si a - b = 0.

Contrairement à la multiplication des nombres ordinaires, où si ab = ac, alors b est toujours égal à c sauf si a est zéro, le produit des points n'obéit pas à la loi d'annulation :

Si a - b = a - c et a ≠ 0, alors nous pouvons écrire : a - (b - c) = 0 par la loi de répartition ; le résultat ci-dessus indique que cela signifie simplement que a est perpendiculaire à (b - c), ce qui permet toujours (b - c) ≠ 0, et donc b ≠ c.

À condition que la base soit orthonormée, le produit scalaire est invariant sous l'effet des changements isométriques de la base : rotations, réflexions et combinaisons, en gardant l'origine fixe. L'interprétation géométrique mentionnée ci-dessus repose sur cette propriété. En d'autres termes, pour un espace orthonormé ayant un nombre quelconque de dimensions, le produit scalaire est invariant sous une transformation de coordonnées basée sur une matrice orthogonale. Cela correspond aux deux conditions suivantes :

• La nouvelle base est à nouveau orthonormée (c'est-à-dire qu'elle est orthonormée exprimée dans l'ancienne).
• Les nouveaux vecteurs de base ont la même longueur que les anciens (c'est-à-dire une longueur unitaire par rapport à l'ancienne base).

Si a et b sont des fonctions, alors la dérivée de a - b est a' - b + a - b'.

Triple expansion des produits

Il s'agit d'une identité très utile (également connue sous le nom de formule de Lagrange) impliquant les points et les produits croisés. Elle s'écrit

a × ( b × c ) = b ( a ⋅ c ) - c ( a ⋅ b ) {\displaystyle \mathbf {a} \times (\mathbf {b} \times \mathbf {c} )=\mathbf {b} (\mathbf {a} \cdot \mathbf {c} )-\mathbf {c} (\mathbf {a} \cdot \mathbf {b} )}

qui est plus facile à retenir comme "BAC moins CAB", en gardant à l'esprit les vecteurs qui sont pointillés ensemble. Cette formule est couramment utilisée pour simplifier les calculs vectoriels en physique.

Preuve de l'interprétation géométrique

Considérons l'élément de Rn

v = v 1 e ^ 1 + v 2 e ^ 2 + ... + v n e ^ n . {\displaystyle \mathbf {v} =v_{1}\mathbf {\hat {e}} _{1}+v_{2}\mathbf {\hat {e}}} _{2}+...+v_{n}\mathbf {\hat {e}} _{n}.\,}

L'application répétée du théorème de Pythagore donne des rendements pour sa longueur |v|

| v | 2 = v 1 2 + v 2 2 + ... + v n 2 . {\displaystyle |\mathbf {v} |^{2}=v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2}.\,}

Mais c'est la même chose que

v ⋅ v = v 1 2 + v 2 2 + ... + v n 2 , {\displaystyle \mathbf {v} \cdot \mathbf {v} =v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2},\,}

Nous en concluons donc que le fait de prendre le produit scalaire d'un vecteur v avec lui-même donne la longueur au carré du vecteur.

Lemma 1

v ⋅ v = | v | 2 . {\displaystyle \mathbf {v} \cdot \mathbf {v} =|\mathbf {v} |^{2}.\,}

Considérons maintenant deux vecteurs a et b s'étendant depuis l'origine, séparés par un angle θ. Un troisième vecteur c peut être défini comme

c = d e f a - b . {\displaystyle \mathbf {c} \\N - \N - \N - \N }{=}}\ \mathbf {a} -\mathbf {b} .\,}

créant un triangle avec les côtés a, b et c. Selon la loi des cosinus, nous avons

| c | 2 = | a | 2 + | b | 2 - 2 | a | | b | cos θ . {\displaystyle |\mathbf {c} |^{2}=|\mathbf {a} |^{2}+|\mathbf {b} |^{2}-2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,}

En substituant les produits de points aux longueurs au carré selon Lemma 1, on obtient

c ⋅ c = a ⋅ a + b ⋅ b - 2 | a | | b | cos θ . {\displaystyle \mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,} (1)

Mais comme c ≡ a - b, nous avons aussi

c ⋅ c = ( a - b ) ⋅ ( a - b ) {\displaystyle \mathbf {c} \cdot \mathbf {c} =(\mathbf {a} -\mathbf {b} )\cdot (\mathbf {a} -\mathbf {b} )\,} ,

qui, selon le droit de la distribution, s'étend à

c ⋅ c = a ⋅ a + b ⋅ b - 2 ( a ⋅ b ) . {\displaystyle \mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} ).\,} (2)

En fusionnant les deux équations c - c, (1) et (2), on obtient

a ⋅ a + b ⋅ b - 2 ( a ⋅ b ) = a ⋅ a + b ⋅ b - 2 | a | | b | cos θ . {\displaystyle \mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} )=\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,}

En soustrayant a - a + b - b des deux côtés et en divisant par -2 feuilles

a ⋅ b = | a | | b | cos θ . {\displaystyle \mathbf {a} \cdot \mathbf {b} =|\mathbf {a} ||\mathbf {b} |\cos \theta .\,}

Q.E.D.

Généralisation

Le produit intérieur généralise le produit ponctuel à des espaces vectoriels abstraits et est généralement désigné par ⟨ a , b ⟩ {\displaystyle \langle \mathbf {a} \,,\mathbf {b} \rangle } . En raison de l'interprétation géométrique du produit scalaire, la norme ||a|| d'un vecteur a dans un tel espace de produit intérieur est définie comme suit

‖ a ‖ = ⟨ a , a ⟩ {\displaystyle \|\mathbf {a} \|={\sqrt {\langle \mathbf {a} \,,\mathbf {a} \rangle }}}

de telle sorte qu'il généralise la longueur, et l'angle θ entre deux vecteurs a et b par

cos θ = ⟨ a , b ⟩ ‖ a ‖ ‖ b ‖ . Displaystyle \cos \theta }={\frac \langle \mathbf {a} \,,\mathbf {b} \rangle }{\|\mathbf {a} \|\,\|\mathbf {b} \|}}. }

En particulier, deux vecteurs sont considérés comme orthogonaux si leur produit intérieur est égal à zéro

⟨ a , b ⟩ = 0. {\displaystyle \langle \mathbf {a} \,,\mathbf {b} \rangle =0.}

Pour les vecteurs à entrées complexes, l'utilisation de la définition donnée du produit scalaire conduirait à des propriétés géométriques très différentes. Par exemple, le produit scalaire d'un vecteur avec lui-même peut être un nombre complexe arbitraire, et peut être nul sans que le vecteur soit le vecteur zéro ; cela aurait à son tour de graves conséquences pour des notions comme la longueur et l'angle. De nombreuses propriétés géométriques peuvent être récupérées, au prix de l'abandon des propriétés symétriques et bilinéaires du produit scalaire, en définissant alternativement

a ⋅ b = ∑ a i b i ¯ {\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum {a_{i}{\overline {b_{i}}}}}

où _{bi est} le conjugué complexe de _bi. Alors le produit scalaire de tout vecteur avec lui-même est un nombre réel non négatif, et il est non nul sauf pour le vecteur zéro. Cependant, ce produit scalaire n'est pas linéaire en b (mais plutôt linéaire conjugué), et le produit scalaire n'est pas non plus symétrique, puisque

a ⋅ b = b ⋅ a ¯ {\displaystyle \mathbf {a} \cdot \mathbf {b} ={\overline \mathbf {b} \cdot \mathbf {a} }}} .

Ce type de produit scalaire est néanmoins très utile, et conduit aux notions de forme hermitienne et d'espaces intérieurs généraux du produit.

Le produit intérieur de Frobenius généralise le produit ponctuel aux matrices. Il est défini comme la somme des produits des composants correspondants de deux matrices ayant la même taille.

Généralisation aux tenseurs

Le produit du point entre un tenseur d'ordre n et un tenseur d'ordre m est un tenseur d'ordre n+m-2. Le produit scalaire est calculé en multipliant et en additionnant un seul indice dans les deux tenseurs. Si A {\displaystyle \mathbf {A} } et B {\displaystyle \mathbf {B} } sont deux tenseurs avec représentation des éléments A i j ... k ℓ ... {\displaystyle A_{ij\dots }^{k\ell \dots }} et B m n ... p ... i {\displaystyle B_{mn\dots }^{p{\dots }i}} les éléments du produit point A ⋅ B {\displaystyle \mathbf {A} \cdot \mathbf {B} } sont donnés par

A i j ... k ℓ ... B m n ... p ... i = ∑ i = 1 n A i j ... k ℓ ... B m n ... p ... i {\displaystyle A_{ij\dots B_{mn{dots }^{k\ell \dots }^{p{\dots }i}=\somme _{i=1}^{n}A_{ij\dots }^{k\ell \dots }B_{mn{\dots }^{p{\dots }i}}}

Cette définition se réduit naturellement au produit vectoriel standard des points lorsqu'elle est appliquée aux vecteurs, et à la multiplication des matrices lorsqu'elle est appliquée aux matrices.

Parfois, un produit à double point est utilisé pour représenter la multiplication et la somme de deux indices. Le produit double point entre deux tenseurs d'ordre 2 est un scalaire.

Pages connexes

• L'inégalité Cauchy-Schwarz
• Produit croisé
• Multiplication matricielle
• Physique