Dimension
Les dimensions sont la façon dont nous voyons, mesurons et vivons notre monde. En utilisant le haut et le bas, de droite à gauche, de l'arrière à l'avant, le chaud et le froid, le poids et la longueur ainsi que des concepts plus avancés des mathématiques et de la physique. Une façon de définir une dimension est d'examiner les degrés de liberté ou la façon dont un objet peut se déplacer dans un espace spécifique. Il existe différents concepts ou différentes façons d'utiliser le terme "dimension" et il existe également différentes définitions. Il n'existe pas de définition qui puisse satisfaire tous les concepts.
Dans un espace vectoriel, (un vecteur est une ligne ouverte à son extrémité), une dimension est égale à la cardinalité ou au nombre de directions des vecteurs ou des lignes. Elle est également égale au nombre du plus grand groupe de directions de lignes droites de cet espace. Les objets "normaux" de la vie quotidienne sont spécifiés par trois dimensions, qui sont généralement appelées longueur, largeur et profondeur. Les mathématiciens appellent ce concept "espace euclidien".
Les dimensions peuvent également être utilisées pour mesurer la position. La distance à une position par rapport à un point de départ peut être mesurée dans les directions de la longueur, de la largeur et de la hauteur. Ces distances sont une mesure de la position.
Parfois, une quatrième dimension (4D), le temps, est utilisée pour montrer la position d'un événement dans le temps et l'espace.
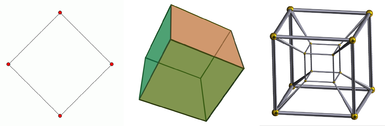
De gauche à droite, le carré, le cube et le tesson. Le carré est un objet à deux dimensions, le cube est un objet à trois dimensions et le tesson est un objet à quatre dimensions. Un objet à une dimension n'est qu'une ligne. Une projection du cube est donnée puisqu'il est visualisé sur un écran bidimensionnel. Il en va de même pour le tesseract, qui ne peut en outre être représenté que sous forme de projection, même dans un espace tridimensionnel.

Un diagramme des quatre premières dimensions spatiales.
Autres dimensions
Dans la science moderne, les gens utilisent d'autres dimensions. Des dimensions comme la température et le poids peuvent être utilisées pour montrer la position de quelque chose dans des espaces moins simples. Les scientifiques étudient ces dimensions grâce à l'analyse dimensionnelle.
Les mathématiciens utilisent également les dimensions. En mathématiques, les dimensions sont plus générales. En mathématiques, les dimensions ne mesurent pas forcément les choses du monde. Les règles pour faire de l'arithmétique avec des dimensions en mathématiques peuvent être différentes des règles arithmétiques habituelles.
Dimensions et vecteurs
Les vecteurs sont utilisés pour indiquer les distances et les directions. Les vecteurs sont souvent utilisés en ingénierie et en sciences, et parfois en mathématiques.
Un vecteur est une liste de nombres. Il y a un nombre pour chaque dimension. Il existe des règles arithmétiques pour les vecteurs.
Par exemple, si Jane veut connaître la position de Sally, Sally peut donner à Jane un vecteur pour montrer la position. Si Jane et Sally sont dans le monde, il y a trois dimensions. Par conséquent, Sally donne à Jane une liste de trois chiffres pour montrer sa position. Les trois nombres du vecteur que Sally donne à Jane pourraient être :
- La distance de Sally au nord de Jane
- La distance de Sally à l'est de Jane
- La hauteur de Sally au-dessus de Jane
Questions et réponses
Q : Qu'est-ce qu'une dimension ?
R : Une dimension est une façon de mesurer, de voir et d'expérimenter le monde en utilisant des concepts tels que le haut et le bas, la droite et la gauche, l'arrière et l'avant, le chaud et le froid, le poids et la longueur. Elle peut également être définie comme les degrés de liberté ou la façon dont un objet peut se déplacer dans un espace spécifique.
Q : Comment les mathématiciens définissent-ils l'espace euclidien ?
R : Les mathématiciens définissent l'espace euclidien comme étant spécifié par trois dimensions qui sont généralement appelées longueur, largeur et profondeur.
Q : Quel est le nombre de vecteurs dans un espace vectoriel ?
R : Le nombre de vecteurs dans un espace vectoriel est égal à la cardinalité (ou nombre de vecteurs) de son ensemble de base.
Q : Combien de dimensions sont utilisées pour mesurer la position ?
R : Trois dimensions (longueur, largeur et hauteur) sont utilisées pour mesurer la position. Dans certaines occasions, une quatrième dimension (4D) - le temps - peut être utilisée pour montrer la position d'un événement dans le temps et l'espace.
Q : Que signifie dim(V) ?
R : Dim(V) fait référence à la dimension de V qui est égale à la cardinalité (ou nombre de vecteurs) de son ensemble de base ou égale au nombre de directions de lignes droites qu'il possède.
Q : Existe-t-il une définition unique qui satisfait tous les concepts liés aux dimensions ?
R : Non, il n'existe pas de définition unique qui puisse satisfaire tous les concepts liés aux dimensions.
Rechercher dans l'encyclopédie