Calcul différentiel

Le calcul différentiel, une branche du calcul, est le processus qui consiste à déterminer le taux de variation d'une variable par rapport à une autre variable, en utilisant des fonctions. C'est un moyen de découvrir comment une forme change d'un point à l'autre, sans avoir besoin de diviser la forme en un nombre infini de morceaux. Le calcul différentiel est l'opposé du calcul intégral. Il a été développé dans les années 1670 et 1680 par Sir Isaac Newton et Gottfried Leibniz.

Contexte

Contrairement à un nombre tel que 5 ou 200, une variable peut changer de valeur. Par exemple, la distance et le temps sont des variables. Lors d'une course à pied olympique, la distance entre la personne et la ligne de départ augmente au fur et à mesure qu'elle court. Pendant ce temps, un chronomètre ou une horloge mesure le temps au fur et à mesure qu'il augmente. Nous pouvons mesurer la vitesse moyenne du coureur si nous divisons la distance qu'il a parcourue par le temps qu'il a mis. Mais cela ne dit pas à quelle vitesse la personne courait exactement 1,5 seconde après le début de la course. Si nous avions la distance à 1 seconde et la distance à 2 secondes, nous n'aurions toujours qu'une moyenne, même si elle serait probablement plus correcte que la moyenne de l'ensemble de la course.

Jusqu'à l'invention du calcul, la seule façon de résoudre ce problème était de réduire le temps en morceaux de plus en plus petits, de sorte que la vitesse moyenne sur le temps le plus court se rapproche de plus en plus de la vitesse réelle à exactement 1,5 seconde. C'était un processus très long et difficile, qui devait être effectué chaque fois que les gens voulaient trouver une solution. Imaginez un conducteur essayant de calculer la vitesse d'une voiture en utilisant uniquement son compteur kilométrique et son horloge, sans compteur de vitesse !

Un problème très similaire consiste à trouver la pente (sa valeur) en tout point d'une courbe. La pente d'une ligne droite est facile à calculer : il suffit de diviser la pente ascendante (y ou verticale) par la pente transversale (x ou horizontale). Si une ligne est parallèle à l'axe des x, sa pente est alors nulle. Si une ligne droite passe par (x,y) = (2,10) et (4,18), la ligne monte de 8 et passe par 2, donc sa pente est de 8 divisé par 2, qui est 4.

Sur une "courbe", cependant, la pente est une variable (elle a des valeurs différentes en différents points) parce que la ligne se courbe. Mais si la courbe devait être coupée en très, très petits morceaux, la courbe au niveau du point ressemblerait presque à une ligne droite très courte. Pour calculer sa pente, on peut donc tracer une ligne droite passant par le point ayant la même pente que la courbe en ce point. Si l'opération est effectuée correctement, la ligne droite aura la même pente que la courbe et sera appelée tangente. Mais il n'y a aucun moyen de savoir (sans calcul) si la tangente est exactement exacte, et nos yeux ne sont pas assez précis pour savoir si elle est exacte ou simplement très proche.

Ce que Newton et Leibniz ont trouvé, c'est un moyen de calculer la pente (ou la vitesse dans l'exemple de la distance) avec précision en utilisant des règles simples et logiques. Ils ont divisé la courbe en un nombre infini de très petits morceaux. Ils ont ensuite choisi des points de chaque côté du point qui les intéressait et ont calculé les tangentes à chacun d'eux. Au fur et à mesure que les points se rapprochaient du point qui les intéressait, la pente s'approchait d'une valeur particulière tandis que les tangentes se rapprochaient de la pente réelle de la courbe. Ils ont dit que cette valeur particulière qu'ils approchaient était la pente réelle.

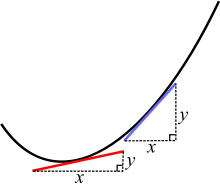
Sur une courbe, deux points différents ont des pentes différentes. Les lignes rouge et bleue sont tangentes à la courbe.

Comment cela fonctionne-t-il ?

Disons que nous avons une fonction y = f(x). f est l'abréviation de function, donc cette équation signifie "y est une fonction de x". Cela nous dit que la hauteur de y sur l'axe vertical dépend de ce que x (l'axe horizontal) est à ce moment. Par exemple, avec l'équation y = x², nous savons que si x est égal à 1, alors y sera égal à 1 ; si x est égal à 3, alors y sera égal à 9 ; si x est égal à 20, alors y sera égal à 400.

Choisissez un point A sur la courbe, et appelez sa position horizontale x. Choisissez ensuite un autre point B sur la courbe qui est un peu plus éloigné de A, et appelez sa position horizontale x + h. Peu importe la valeur de h, c'est un très petit nombre.

Ainsi, lorsque nous allons du point A au point B, la position verticale est passée de f(x) à f(x + h), et la position horizontale est passée de x à x + h. Maintenant, souvenez-vous que la pente est le quotient de sa montée par sa traversée. La pente sera donc :

f ( x + h ) - f ( x ) h {\frac {f(x+h)-f(x)}{h}}} ${\frac {f(x+h)-f(x)}{h}}$

Si vous rapprochez B de plus en plus de A - ce qui signifie que h se rapproche de plus en plus de 0 - alors nous nous rapprochons de la connaissance de la pente au point A.

lim h → 0 f ( x + h ) - f ( x ) h {\displaystyle \lim _{h\rightarrow 0}{\frac {f(x+h)-f(x)}{h}}} $\lim _{h\rightarrow 0}{\frac {f(x+h)-f(x)}{h}}$

Revenons maintenant à y = x². On peut déterminer la pente comme suit :

= lim h → 0 f ( x + h ) - f ( x ) h = lim h → 0 ( x + h ) 2 - ( x ) 2 h {\displaystyle {\begin{aligned}&=\lim _{h\fourchette droite 0}{\frac {f(x+h)-f(x)}{h}}\\&=\lim _{h\fourchette droite 0}{\frac {(x+h)^{2}-(x)^{2}{h}}\end{aligné}}} ${\begin{aligned}&=\lim _{h\rightarrow 0}{\frac {f(x+h)-f(x)}{h}}\\&=\lim _{h\rightarrow 0}{\frac {(x+h)^{2}-(x)^{2}}{h}}\end{aligned}}$

En appliquant le théorème du binôme qui dit ( x + y ) 2 = x 2 + 2 x y + y 2 {\displaystyle (x+y)^{2}=x^{2}+2xy+y^{2}} $(x+y)^{2}=x^{2}+2xy+y^{2}$ nous pouvons réduire à :

= lim h → 0 x 2 + 2 x h + h 2 - x 2 h = lim h → 0 2 x h + h 2 h = lim h → 0 2 x + h = 2 x {\displaystyle}début{\c}&=\lim _{h\fourchette droite 0}{\frac {x^{2}+2xh+h^{2}-x^{2}{h}}\\&=\lim _{h\fourchette droite 0}{\frac {2xh+h^{2}{h}}\\&=\lim _{h\fourchette droite 0}2x+h\\\&={\frac {}{}{}}2x\end{aligned}}} ${\begin{aligned}&=\lim _{h\rightarrow 0}{\frac {x^{2}+2xh+h^{2}-x^{2}}{h}}\\&=\lim _{h\rightarrow 0}{\frac {2xh+h^{2}}{h}}\\&=\lim _{h\rightarrow 0}2x+h\\&={\frac {}{}}2x\end{aligned}}$

Nous savons donc, sans avoir à tracer de lignes tangentes, qu'en tout point de la courbe f(x) = x², la dérivée f'(x) (marquée d'une apostrophe) sera de 2x en tout point. Ce processus d'élaboration d'une pente à l'aide de limites est appelé différenciation, ou recherche de la dérivée.

Leibniz est arrivé au même résultat, mais a appelé h "dx", qui signifie "une quantité infime de x". Il a appelé le changement résultant de f(x) "dy", ce qui signifie "une quantité minuscule de y". La notation de Leibniz est utilisée dans de nombreux livres car elle est facile à comprendre lorsque les équations deviennent plus complexes. Dans la notation de Leibniz :

d y d x = f ′ ( x ) {\displaystyle {\frac {dy}{dx}}=f'(x)} ${\frac {dy}{dx}}=f'(x)$

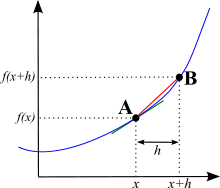
Une image montrant ce que x et x + h signifient sur la courbe.

Règles

En utilisant le système ci-dessus, les mathématiciens ont élaboré des règles qui fonctionnent tout le temps, quelle que soit la fonction examinée. (Note : ici, u {\displaystyle u} $u$ et v {\displaystyle v} $v$ sont tous deux des fonctions de x {\displaystyle x} )

Condition	Fonction	Dérivé	Exemple	Dérivé
Un numéro en soi	y = a {\displaystyle y=a} $y=a$	d y d x = 0 {\frac {dy}{dx}}=0} ${\frac {dy}{dx}}=0$	y = 3 {\displaystyle y=3} $y=3$	0 {\displaystyle 0} $0$
Une ligne droite	y = m x + c {\displaystyle y=mx+c} $y=mx+c$	d y d x = m {\frac {dy}{dx}}=m} ${\frac {dy}{dx}}=m$	y = 3 x + 5 {\style d'affichage y=3x+5} $y=3x+5$	3 {\displaystyle 3} $3$
x à la puissance d'un nombre	x a {\displaystyle x^{a}} $x^{a}$	d y d x = a x a - 1 {\displaystyle {\frac {dy}{dx}}=ax^{a-1}} ${\frac {dy}{dx}}=ax^{a-1}$	x 12 {\displaystyle x^{12}} $x^{12}$	12 x 11 {\displaystyle 12x^{11}} $12x^{11}$
Un nombre multiplié par une fonction	y = c ⋅ u {\displaystyle y=c\cdot u} $y=c\cdot u$	d y d x = c d u d x x {\displaystyle {\frac {dy}{dx}}=c{\frac {du}{dx}}} ${\frac {dy}{dx}}=c{\frac {du}{dx}}$	y = 3 ( x 2 + x ) {\displaystyle y=3(x^{2}+x)} $y=3(x^{2}+x)$	3 ( 2 x + 1 ) {\displaystyle 3(2x+1)} $3(2x+1)$
Une fonction plus une autre fonction	y = u + v {\displaystyle y=u+v} $y=u+v$	d y d x = d u d x + d v d x {\displaystyle {\frac {dy}{dx}}={\frac {du}{dx}}+{\frac {dv}{dx}}}} ${\frac {dy}{dx}}={\frac {du}{dx}}+{\frac {dv}{dx}}$	y = 3 x 2 + x {\displaystyle y=3x^{2}+{\sqrt {x}}} $y=3x^{2}+{\sqrt {x}}$	6 x + 1 x {\displaystyle 6x+{\frac {1}{\sqrt {x}}}} $6x+{\frac {1}{\sqrt {x}}}$
Une fonction moins une autre fonction	y = u - v {\displaystyle y=u-v} $y=u-v$	d y d x = d u d x - d v d x {\displaystyle {\frac {dy}{dx}}={\frac {du}{dx}}-{\frac {dv}{dx}}} ${\frac {dy}{dx}}={\frac {du}{dx}}-{\frac {dv}{dx}}$	y = 3 x 2 - x {\displaystyle y=3x^{2}-{\sqrt {x}}} $y=3x^{2}-{\sqrt {x}}$	6 x - 1 x {\displaystyle 6x-{\frac {1}{\sqrt {x}}}} $6x-{\frac {1}{\sqrt {x}}}$
Product RuleUne fonction multipliée par une autre fonction	y = u ⋅ v {\displaystyle y=u\cdot v} $y=u\cdot v$	d y d x = d u d x v + u d v d x {\displaystyle {\frac {dy}{dx}}={\frac {du}{dx}}v+u{\frac {dv}{dx}}} ${\frac {dy}{dx}}={\frac {du}{dx}}v+u{\frac {dv}{dx}}$	y = ( x 2 + x + 2 ) ( 3 x - 1 ) {\displaystyle y=(x^{2}+x+2)(3x-1)} $y=(x^{2}+x+2)(3x-1)$	( 3 x - 1 ) ( 2 x + 1 ) + 3 ( x 2 + x + 2 ) {\displaystyle (3x-1)(2x+1)+3(x^{2}+x+2)} $(3x-1)(2x+1)+3(x^{2}+x+2)$
Règle du quotientUne fonction divisée par une autre fonction	y = u v {\displaystyle y={\frac {u}{v}}} $y={\frac {u}{v}}$	d y d x = d u d x v - u d v d x v 2 {\displaystyle {\frac {dy}{dx}}={\frac {{\frac {du}{dx}}}v-u{\frac {dv}{dx}}} {v^{2}}}} ${\frac {dy}{dx}}={\frac {{\frac {du}{dx}}v-u{\frac {dv}{dx}}}{v^{2}}}$	y = x 2 + 2 x - 1 {\displaystyle y={\frac {x^{2}+2}{x-1}}} $y={\frac {x^{2}+2}{x-1}}$	2 x ( x - 1 ) - ( x 2 + 2 ) ( x - 1 ) 2 {\displaystyle {\frac {2x(x-1)-(x^{2}+2)}{(x-1)^{2}}}} ${\frac {2x(x-1)-(x^{2}+2)}{(x-1)^{2}}}$
Règle de la chaîne Utilisé pour les fonctions composites	y = u ∘ v {\displaystyle y=u\circ v} $y=u\circ v$	d y d x = d y d u ⋅ d u d x {\displaystyle {\frac {dy}{dx}}={\frac {dy}{du}}\cdot {\frac {du}{dx}}} ${\frac {dy}{dx}}={\frac {dy}{du}}\cdot {\frac {du}{dx}}$	y = 2 x - 1 {\displaystyle y={\sqrt {2x-1}}} $y={\sqrt {2x-1}}$	2 2 2 x - 1 = 1 2 x - 1 {\frac {2}{2{\sqrt {2x-1}}}}={\frac {1}{\sqrt {2x-1}}}} ${\frac {2}{2{\sqrt {2x-1}}}}={\frac {1}{\sqrt {2x-1}}}$
Une fonction exponentielle	y = e x {\displaystyle {\frac {}{}}}y=e^{x}} ${\frac {}{}}y=e^{x}$	d y d x = e x {\displaystyle {\frac {dy}{dx}}=e^{x}} ${\frac {dy}{dx}}=e^{x}$	y = e x {\displaystyle {\frac {}{}}}y=e^{x}} ${\frac {}{}}y=e^{x}$	e x {\displaystyle {\frac {}{}}}e^{x}} ${\frac {}{}}e^{x}$

Questions et réponses

Q : Qu'est-ce que le calcul différentiel ?

R : Le calcul différentiel est une branche du calcul qui étudie le taux de variation d'une variable par rapport à une autre variable, en utilisant des fonctions.

Q : Comment cela fonctionne-t-il ?

R : Le calcul différentiel nous permet de découvrir comment une forme change d'un point à un autre sans avoir besoin de diviser la forme en un nombre infini de morceaux.

Q : Qui a développé le calcul différentiel ?

R : Le calcul différentiel a été développé dans les années 1670 et 1680 par Sir Isaac Newton et Gottfried Leibniz.

Q : Qu'est-ce que le calcul intégral ?

R : Le calcul intégral est l'opposé du calcul différentiel. Il est utilisé pour trouver les aires sous les courbes et les volumes des solides avec des surfaces courbes.

Q : Quand le calcul différentiel a-t-il été développé ?