Problème de décision
Dans la théorie de la calculabilité et la théorie de la complexité informatique, un problème de décision est une question dans un système formel avec une réponse par oui ou par non. La réponse dépend des valeurs des paramètres d'entrée. Les problèmes de décision apparaissent généralement dans les questions mathématiques de décidabilité, c'est-à-dire la question de l'existence d'une méthode efficace pour déterminer l'existence d'un objet ou son appartenance à un ensemble. Certains des problèmes les plus importants en mathématiques sont indécidables.
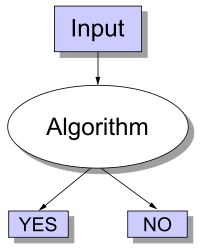
Un problème de décision n'a que deux sorties possibles, oui ou non (ou alternativement 1 ou 0) sur une entrée.
Questions et réponses
Q : Qu'est-ce qu'un problème de décision ?
R : Un problème de décision est une question dans un système formel avec une réponse oui ou non, dépendant des valeurs des paramètres d'entrée.
Q : Dans quels domaines d'étude les problèmes de décision apparaissent-ils ?
R : Les problèmes de décision apparaissent généralement dans les questions mathématiques de décidabilité.
Q : Que signifie le terme "décidabilité" ?
R : La décidabilité fait référence à la question de l'existence d'une méthode efficace pour déterminer l'existence d'un objet ou son appartenance à un ensemble.
Q : Tous les problèmes mathématiques sont-ils décidables ?
R : Non, certains des problèmes les plus importants en mathématiques sont indécidables.
Q : Qu'est-ce qu'un problème indécidable ?
R : Un problème indécidable est un problème pour lequel il n'existe pas d'algorithme qui puisse toujours fournir une réponse par oui ou par non en un temps fini.
Q : La réponse à un problème de décision est-elle toujours oui ou non ?
R : Oui, la réponse à un problème de décision est toujours oui ou non.
Q : De quoi dépend la réponse à un problème de décision ?
R : La réponse à un problème de décision dépend des valeurs des paramètres d'entrée.
Rechercher dans l'encyclopédie