Algorithme

Comparaison des algorithmes

Il y a généralement plus d'une façon de résoudre un problème. Il peut y avoir de nombreuses recettes différentes pour réaliser un certain plat qui a une apparence différente mais qui finit par avoir le même goût au bout du compte. Il en va de même pour les algorithmes. Toutefois, certaines de ces méthodes seront meilleures que d'autres. Si une recette nécessite beaucoup d'ingrédients compliqués que vous n'avez pas, elle n'est pas aussi bonne qu'une recette simple. Lorsque nous considérons les algorithmes comme un moyen de résoudre des problèmes, nous voulons souvent savoir combien de temps il faudrait à un ordinateur pour résoudre le problème en utilisant un algorithme particulier. Lorsque nous écrivons des algorithmes, nous aimons que notre algorithme prenne le moins de temps possible pour que nous puissions résoudre notre problème le plus vite possible.

En cuisine, certaines recettes sont plus difficiles à réaliser que d'autres, car elles prennent plus de temps à réaliser ou ont plus de choses à suivre. Il en va de même pour les algorithmes, et les algorithmes sont meilleurs lorsqu'ils sont plus faciles à réaliser par l'ordinateur. La chose qui mesure la difficulté d'un algorithme s'appelle la complexité. Lorsque nous demandons à quel point un algorithme est complexe, nous voulons souvent savoir combien de temps il faudra à un ordinateur pour résoudre le problème que nous voulons qu'il résolve.

Triage

Il s'agit d'un exemple d'algorithme permettant de trier les cartes avec des couleurs en piles de la même couleur :

1. Ramassez toutes les cartes.
2. Choisissez une carte dans votre main et regardez la couleur de la carte.
3. S'il y a déjà une pile de cartes de cette couleur, mettez cette carte sur cette pile.
4. S'il n'y a pas de pile de cartes de cette couleur, faites une nouvelle pile de cartes de cette couleur uniquement.
5. S'il vous reste une carte en main, revenez à la deuxième étape.
6. S'il n'y a pas encore de carte en main, les cartes sont triées. Vous avez terminé.

Tri par numéros

Ce sont des exemples d'algorithmes permettant de trier une pile de cartes avec de nombreux numéros différents, de manière à ce que les numéros soient en ordre.

Les joueurs commencent avec une pile de cartes qui n'ont pas été triées.

Premier algorithme

Cet algorithme passe par la pile de cartes, une carte à la fois. Cette carte est comparée à la carte suivante de la pile. Veuillez noter que cette position ne change qu'à l'étape 6. Cet algorithme est appelé "tri à bulles". Il est lent.

1. Si la pile de cartes est vide, ou si elle ne contient qu'une seule carte, elle est triée ; vous avez terminé.
2. Prenez la pile de cartes. Regardez la première carte (le haut) de la pile.
3. La carte que vous regardez est la carte A. La position où se trouve actuellement la carte A, est dans la pile P.
4. S'il n'y a plus de cartes dans la pile après la carte A, passez à l'étape 8.
5. La carte suivante dans la pile est la carte B.
6. Si la carte B a un numéro inférieur à celui de la carte A, échangez les positions des cartes A et B. N'oubliez pas que c'est vous qui avez fait cela. Lorsque vous échangez des cartes, ne changez pas la position de la carte P.
7. S'il y a une autre carte dans la pile après la position P, regardez-la ; retournez à l'étape 3.
8. Si vous n'avez pas échangé la position des cartes lors du dernier tour, vous avez terminé ; la pile de cartes est triée.
9. Sinon, retournez à l'étape 2.

Un exemple pas à pas

Prenons une pile de cartes avec les nombres "5 1 4 2 8", et trions la carte du plus petit au plus grand nombre en utilisant cet algorithme. À chaque étape, l'algorithme compare les éléments écrits en gras. Le haut de la pile de cartes se trouve sur le côté gauche.

Premier passage :
( 5 1 4 2 8 ) → {\displaystyle \to } ( 1 5 4 2 8 ) Ici, l'algorithme compare les deux premiers éléments et les échange.
( 1 5 4 2 8 ) → {\displaystyle \to } ( 1 4 5 2 8 )(
 1 4 5 2 8 ) → {\displaystyle \to } ( 1 4 2 5 8 )(
 1 4 2 5 8 ) → {\displaystyle \to } ( 1 4 2 5 8 ) Ces éléments sont déjà en ordre, donc l'algorithme ne les échange pas.
Deuxième passage :
( 1 4 2 5 8 ) → {\displaystyle \to } ( 1 4 2 5 8 )(
 1 4 2 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )(
 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )(
 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
Maintenant, la pile de cartes est déjà triée, mais notre algorithme ne le sait pas. L'algorithme a besoin d'un passage complet sans échange pour savoir qu'il est trié.
Troisième passage :
( 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )(
 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )(
 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )(
 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
Enfin, le tableau est trié, et l'algorithme peut s'arrêter.

Histoire

Il s'agit d'un algorithme de tri facile à comprendre. Les informaticiens l'ont appelé tri à bulles, car les éléments les plus petits montent au sommet, changeant leur position à chaque passage. Malheureusement, l'algorithme n'est pas très bon, car il faut beaucoup de temps (beaucoup passent dans la pile de cartes) pour le trier.

Deuxième algorithme

Cet algorithme utilise une autre idée. Il est parfois difficile de résoudre un problème, mais le problème peut être modifié de manière à ce qu'il soit composé de problèmes plus simples et plus faciles à résoudre. C'est ce qu'on appelle la récursion. Il est plus difficile à comprendre que le premier exemple, mais il donnera un meilleur algorithme.

Idée de base

1. Si la pile ne contient pas de cartes ou n'en contient qu'une seule, elle est triée et vous avez terminé.
2. Séparez la pile de cartes en deux moitiés de même taille environ. S'il y a un nombre impair de cartes, une des deux piles aura une carte de plus que l'autre.
3. Triez chacune des deux piles à l'aide de cet algorithme (Pour chaque pile, commencez au point 1 de cette liste).
4. Fusionnez les deux piles triées ensemble, comme décrit ci-dessous.
5. Le résultat est une pile de cartes triées. Vous avez terminé.

Fusionner deux piles ensemble

Cela fonctionne avec deux piles de cartes. L'une d'elles s'appelle A, l'autre B. Il y a une troisième pile qui est vide au début, appelée C. À la fin, elle contiendra le résultat.

1. Si la pile A ou la pile B est vide, placez toutes les cartes de la pile qui n'est pas vide sur la pile C ; vous avez terminé, la pile C est le résultat de la fusion. (Note : prenez toute la pile, et mettez-la sur la pile C ; le faire carte par carte changera l'ordre et ne fonctionnera pas comme il se doit).
2. Regardez les cartes du haut de la pile A et de la pile B. Placez celle qui porte le numéro le plus bas sur la pile C. Si la pile C ne contenait aucune carte, elle n'en aura plus qu'une.
3. Si la pile A ou la pile B a encore des cartes, retournez à l'étape 1 pour les trier.

Histoire

John von Neumann a développé cet algorithme en 1945. Il ne l'a pas appelé Tri par numéros, mais Mergesort. C'est un très bon algorithme de tri, comparé à d'autres.

Troisième algorithme

Le premier algorithme prend beaucoup plus de temps que le second pour trier les cartes, mais il peut être amélioré (rendu meilleur). En examinant le tri par bulles, on peut remarquer que les cartes avec des nombres élevés se déplacent du haut de la pile assez rapidement, mais que les cartes avec des nombres faibles en bas de la pile mettent beaucoup de temps à monter (se déplacer vers le haut). Pour améliorer le premier algorithme, voici l'idée :

Plutôt que de comparer deux cartes côte à côte, on choisit au départ une carte "spéciale". Toutes les autres cartes sont ensuite comparées à cette carte.

1. Nous commençons par une pile A. Il y aura deux autres piles B et C, qui seront créées plus tard.
2. Si la pile A n'a pas de cartes, ou n'en a qu'une seule, le tri est terminé.
3. Une carte est prélevée sur la pile A, si possible au hasard. C'est ce qu'on appelle un pivot.
4. Toutes les cartes restantes de la pile A sont comparées à ce pivot. Les cartes avec un nombre inférieur vont dans la pile B, celles avec un nombre égal ou supérieur vont dans la pile C.
5. S'il y a des cartes dans les piles B ou C, ces piles doivent être triées avec le même algorithme (Commencez à la pos. 1 de cette liste pour les piles B et C à tour de rôle).
6. C'est fait. La pile de cartes triée comporte d'abord la pile triée B, puis le pivot, et enfin la pile triée C.

Histoire

Cet algorithme a été développé par C. A. R. Hoare en 1960. C'est aujourd'hui l'un des algorithmes de tri les plus utilisés. Il est appelé Quicksort.

Animation qui montre comment fonctionne un tri à bulles


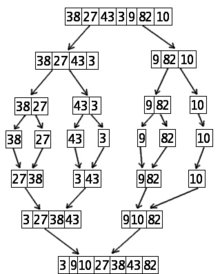
Tri de 7 numéros à l'aide du deuxième algorithme de tri par numéros (Mergesort)


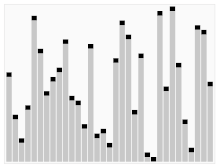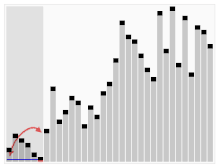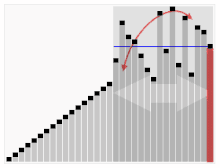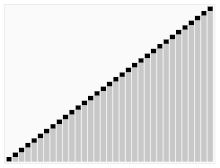
Le troisième algorithme de tri des cartes. L'élément avec la barre rouge est choisi comme pivot. Au début, c'est l'élément tout à droite. Cet algorithme est appelé Quicksort.

Mise au point d'algorithmes

Si les joueurs ont des cartes avec des couleurs et des numéros, ils peuvent les trier par couleur et par numéro s'ils font l'algorithme de "tri par couleurs", puis faire l'algorithme de "tri par numéros" pour chaque pile de couleur, puis assembler les piles.

Les algorithmes de tri par numéros sont plus difficiles à réaliser que l'algorithme de tri par couleurs, car ils peuvent devoir refaire les étapes plusieurs fois. On pourrait dire que le tri par numéros est plus complexe.

Pages connexes

• L'algorithme euclidien a été découvert il y a plus de 2000 ans. Il est capable de trouver le plus grand diviseur commun de deux nombres.