Algèbre

Histoire

Les premières formes d'algèbre ont été développées par les Babyloniens et les géomètres grecs comme Héro d'Alexandrie. Cependant, le mot "algèbre" est une forme latine du mot arabe Al-Jabr ("casting") et vient d'un livre de mathématiques Al-Maqala fi Hisab-al Jabr wa-al-Muqabilah, ("Essai sur le calcul du casting et de l'équation") écrit au 9e siècle par un mathématicien persan, Muhammad ibn Mūsā al-Khwārizmī, qui était un musulman né à Khwarizm en Ouzbékistan. Il a prospéré sous Al-Ma'moun à Bagdad, en Irak, jusqu'en 813-833 après J.-C., et est mort vers 840 après J.-C. Il a été introduit en Europe et traduit en latin au XIIe siècle. Le livre a alors reçu le nom d'"Algèbre". (La terminaison du nom du mathématicien, al-Khwarizmi, a été changée en un mot plus facile à dire en latin, et est devenue le mot anglais algorithm).

Exemples

Voici un exemple simple d'un problème d'algèbre :

Sue a 12 bonbons, et Ann en a 24. Elles décident de partager pour avoir le même nombre de bonbons. Combien de bonbons chacun aura-t-il ?

Voici les étapes que vous pouvez suivre pour résoudre le problème :

1. Pour avoir le même nombre de bonbons, Ann doit en donner à Sue. Soit x représente le nombre de bonbons qu'Ann donne à Sue.
2. Les bonbons de Sue, plus x, doivent être identiques aux bonbons d'Ann moins x. Ceci s'écrit comme : 12 + x = 24 - x
3. Soustrayez 12 des deux côtés de l'équation. Cela donne : x = 12 - x. (Ce qui se passe d'un côté du signe des égaux doit se produire de l'autre côté également, pour que l'équation soit toujours vraie. Donc, dans ce cas, lorsque 12 a été soustrait des deux côtés, il y a eu une étape intermédiaire de 12 + x - 12 = 24 - x - 12. Lorsqu'une personne est à l'aise avec cela, l'étape du milieu n'est pas écrite).
4. Ajoutez x aux deux côtés de l'équation. Cela donne : 2x = 12
5. Divisez les deux côtés de l'équation par 2, ce qui donne x = 6. La réponse est six. Si Ann donne à Sue 6 bonbons, elles auront le même nombre de bonbons.
6. Pour vérifier cela, replacez 6 dans l'équation originale où x était : 12 + 6 = 24 - 6
7. Cela donne 18=18, ce qui est vrai. Ils ont maintenant chacun 18 bonbons.

Avec la pratique, l'algèbre peut être utilisée lorsque l'on est confronté à un problème trop difficile à résoudre autrement. Des problèmes tels que la construction d'une autoroute, la conception d'un téléphone portable ou la recherche d'un remède pour une maladie nécessitent tous de l'algèbre.

Ecrire l'algèbre

Comme dans la plupart des mathématiques, l'addition de z à y (ou y plus z) s'écrit y + z. La soustraction de z à y (ou y moins z) s'écrit y - z. La division de y par z (ou y sur z : y z) s'écrit y ÷ z ou y/z. y/z est le plus souvent utilisé.

En algèbre, la multiplication de y par z (ou y fois z) peut s'écrire de 4 façons : y × z, y * z, y-z, ou simplement yz. Le symbole de multiplication "×" n'est généralement pas utilisé, car il ressemble trop à la lettre x, qui est souvent utilisée comme variable. De plus, lors de la multiplication d'une expression plus grande, on peut utiliser des parenthèses : y (z+1).

Lorsque nous multiplions un nombre et une lettre en algèbre, nous écrivons le nombre devant la lettre : 5 × y = 5y. Lorsque le nombre est 1, alors le 1 n'est pas écrit car 1 fois n'importe quel nombre est ce nombre (1 × y = y) et il n'est donc pas nécessaire.

En marge, vous ne devez pas utiliser les lettres x ou y en algèbre. Les variables ne sont que des symboles qui signifient un nombre ou une valeur inconnus, vous pouvez donc utiliser n'importe quelle variable. x et y sont cependant les plus courants.

Fonctions et graphiques

Une partie importante de l'algèbre est l'étude des fonctions, puisque les fonctions apparaissent souvent dans des équations que nous essayons de résoudre. Une fonction est comme une machine dans laquelle on peut mettre un nombre (ou des nombres) et en faire sortir un certain nombre (ou des nombres). Lorsqu'on utilise des fonctions, les graphiques peuvent être des outils puissants pour nous aider à étudier les solutions des équations.

Un graphique est une image qui montre toutes les valeurs des variables qui rendent l'équation ou l'inégalité vraie. Généralement, cela est facile à faire lorsqu'il n'y a qu'une ou deux variables. Le graphique est souvent une ligne, et si la ligne ne se plie pas ou ne va pas directement de haut en bas, elle peut être décrite par la formule de base y = mx + b. La variable b est l'ordonnée à l'origine du graphique (où la ligne croise l'axe vertical) et m est la pente ou l'inclinaison de la ligne. Cette formule s'applique aux coordonnées d'un graphique, où chaque point de la ligne est écrit (x, y).

Dans certains problèmes mathématiques comme l'équation d'une droite, il peut y avoir plus d'une variable (x et y dans ce cas). Pour trouver des points sur la droite, on change une variable. La variable qui est modifiée est appelée variable "indépendante". Ensuite, le calcul est effectué pour obtenir un nombre. Le nombre obtenu est appelé la variable "dépendante". La plupart du temps, la variable indépendante s'écrit x et la variable dépendante s'écrit y, par exemple, en y = 3x + 1. Cette variable est souvent placée sur un graphique, en utilisant un axe x (allant à gauche et à droite) et un axe y (allant de haut en bas). Elle peut également être écrite sous la forme d'une fonction : f(x) = 3x + 1. Ainsi, dans cet exemple, nous pourrions mettre 5 pour x et obtenir y = 16. Si on met 2 pour x, on obtient y=7. Et 0 pour x donnerait y=1. Il y aurait donc une ligne passant par les points (5,16), (2,7) et (0,1), comme le montre le graphique de droite.

Si x a une puissance de 1, c'est une ligne droite. S'il est carré ou a une autre puissance, il sera courbé. S'il utilise une inégalité (< ou >), alors une partie du graphique est généralement ombrée, soit au-dessus, soit en dessous de la ligne.

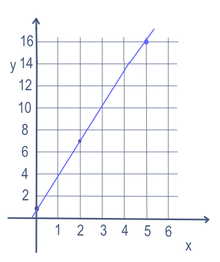
Équation linéaire pour y=3x+1

Règles d'algèbre

En algèbre, il existe quelques règles qui peuvent être utilisées pour mieux comprendre les équations. Ces règles sont appelées les règles de l'algèbre. Bien que ces règles puissent sembler insensées ou évidentes, il est sage de comprendre que ces propriétés ne se retrouvent pas dans toutes les branches des mathématiques. Par conséquent, il sera utile de savoir comment ces règles axiomatiques sont déclarées, avant de les considérer comme allant de soi. Avant de passer aux règles, réfléchissez à deux définitions qui vous seront données.

1. En face, le contraire d'un style d'affichage a est un style d'affichage a.
2. Réciproque - la réciproque d'un style d'affichage a est 1 a un style d'affichage frac {1}{a}} .

Règles

Propriété commutative de l'addition

Commutatif" signifie qu'une fonction a le même résultat si les chiffres sont inversés. En d'autres termes, l'ordre des termes dans une équation n'a pas d'importance. Lorsque l'opérateur de deux termes est une addition, la "propriété commutative de l'addition" est applicable. En termes algébriques, cela donne a + b = b + a.

Notez que cela ne s'applique pas à la soustraction ! (i.e. a - b ≠ b - a a [style d'affichage a-b\neq b-a] )

Propriété commutative de la multiplication

Lorsque l'opérateur de deux termes est une multiplication, la "propriété commutative de la multiplication" est applicable. En termes algébriques, cela donne a ⋅ b = b ⋅ a {\displaystyle a\cdot b=b\cdot a} .

Notez que cela ne s'applique pas à la division ! (i.e. a b ≠ b a a {\displaystyle {\frac {a}{b}}\neq {\frac {b}{a}}} quand a ≠ b {\displaystyle a\neq b} )

Propriété associative de l'addition

Le terme "associatif" fait référence au regroupement des chiffres. La propriété associative de l'addition implique que, lorsque l'on ajoute trois termes ou plus, la manière dont ces termes sont groupés n'a pas d'importance. Algébriquement, cela donne a + ( b + c ) = ( a + b ) + c . Notez que cela n'est pas valable pour la soustraction, par exemple 1 = 0 - ( 0 - 1 ) ≠ ( 0 - 0 ) - 1 = - 1 {\style d'affichage 1=0-(0-1)\neq (0-0)-1=-1} (voir la propriété distributive).

Propriété associative de la multiplication

La propriété associative de la multiplication implique que, lorsque l'on multiplie trois termes ou plus, la façon dont ces termes sont regroupés n'a pas d'importance. Algébriquement, cela donne a ⋅ ( b ⋅ c ) = ( a ⋅ b ) ⋅ c {\displaystyle a\cdot (b\cdot c)=(a\cdot b)\cdot c} . Notez que cela ne vaut pas pour la division, par exemple 2 = 1 / ( 1 / 2 ) ≠ ( 1 / 1 ) / 2 = 1 / 2 {\displaystyle 2=1/(1/2)\neq (1/1)/2=1/2} .

Biens de distribution

La propriété distributive indique que la multiplication d'un nombre par un autre terme peut être distribuée. Par exemple : a ⋅ ( b + c ) = a b + a c {\displaystyle a\cdot (b+c)=ab+ac} . (Ne confondez pas cela avec les propriétés associatives ! Par exemple, a ⋅ ( b + c ) ≠ ( a ⋅ b ) + c {\displaystyle a\cdot (b+c)\neq (a\cdot b)+c} .

Propriété d'identité additive

L'"identité" désigne la propriété d'un nombre qui est égal à lui-même. En d'autres termes, il existe une opération de deux nombres pour qu'il soit égal à la variable de la somme. La propriété additive de l'identité indique que la somme de n'importe quel nombre et de 0 est ce nombre : a + 0 = a {\displaystyle a+0=a} . Cela vaut également pour la soustraction : a - 0 = a {style d'affichage a-0=a} .

Propriété d'identité multiplicative

La propriété d'identité multiplicative indique que le produit d'un nombre quelconque et de 1 est ce nombre : a ⋅ 1 = a {\displaystyle a\cdot 1=a} . Cela vaut également pour la division : a 1 = a {\displaystyle {\frac {a}{1}}=a} .

Propriété additive inverse

La propriété additive inverse est un peu comme l'opposé de la propriété additive d'identité. Lorsqu'une opération est la somme d'un nombre et de son opposé, et qu'elle est égale à 0, cette opération est une opération algébrique valide. Algébriquement, elle indique ce qui suit : a - a = 0 {\displaystyle a-a=0} . L'inverse additif de 1 est (-1).

Propriété inverse multiplicative

La propriété multiplicative inverse implique que lorsqu'une opération est le produit d'un nombre et de sa réciproque, et qu'elle est égale à 1, cette opération est une opération algébrique valide. Algébriquement, elle se présente comme suit : a a = 1 . L'inverse multiplicatif de 2 est 1/2.

Algèbre avancée

En plus de l'"algèbre élémentaire", ou algèbre de base, il existe des formes avancées d'algèbre, enseignées dans les collèges et les universités, telles que l'algèbre abstraite, l'algèbre linéaire et l'algèbre universelle. Il s'agit notamment de savoir comment utiliser une matrice pour résoudre plusieurs équations linéaires à la fois. L'algèbre abstraite est l'étude des choses que l'on trouve dans les équations, allant au-delà des nombres pour aller vers les plus abstraits avec des groupes de nombres.

De nombreux problèmes de mathématiques concernent la physique et l'ingénierie. Dans beaucoup de ces problèmes de physique, le temps est une variable. Le temps utilise la lettre t. L'utilisation des idées de base en algèbre peut aider à réduire un problème mathématique à sa forme la plus simple, ce qui facilite la résolution de problèmes difficiles. L'énergie est e, la force est f, la masse est m, l'accélération est a et la vitesse de la lumière est parfois c. Ceci est utilisé dans certaines équations célèbres, comme f = ma et e=mc^2 (bien que des mathématiques plus complexes au-delà de l'algèbre aient été nécessaires pour arriver à cette dernière équation).

Pages connexes

• Liste des thèmes mathématiques
• Ordre des opérations
• Parabole
• Système d'algèbre informatique