AlegsaOnline.com

Cylindre (géométrie)

Forme géométrique obtenue en extrudant une courbe le long d'une droite : définitions, variantes (circulaire, elliptique, oblique), formules d'aire et de volume, propriétés différentielles, histoire et usages.

Auteur: Leandro Alegsa Date de création: 9 mai 2021 Dernière mise à jour: 20 avril 2026

simple.wikipedia.org · CC BY-SA 3.0

Définition générale

Un cylindre est une surface ou un solide obtenu en déplaçant une courbe plane le long d'une droite parallèle à elle-même. On distingue le cylindre comme surface réglée (généralement infini) formé par une famille de droites parallèles et le cylindre comme solide limité par deux plans parallèles coupant cette surface — on parle alors de cylindre fini ou prisme circulaire lorsque la courbe génératrice est un cercle.

Formules usuelles pour le cylindre droit circulaire

Pour un cylindre droit de base circulaire de rayon r et de hauteur h (axes perpendiculaires aux bases) :

Volume : V = π r² h.
Aire latérale : A_lat = 2 π r h (on peut la voir comme le rectangle de côtés 2πr et h obtenu en déroulant la surface latérale).
Aire totale : A_tot = 2 π r (r + h) (inclut les deux bases).

Pour un cylindre annulaire (coque ou tuyau) de rayons intérieur r et extérieur R et hauteur h, on a V = π (R² − r²) h et A_lat = 2 π (R + r) h seulement si l'on considère les surfaces intérieures et extérieures; souvent on retient A_lat_ext = 2 π R h pour la surface extérieure.

Cas oblique et principe de Cavalieri

Un cylindre oblique conserve la même aire de base que le cylindre droit ayant la même section; son volume est égal à l'aire de la base multipliée par la distance entre les plans qui délimitent les bases (hauteur perpendiculaire aux bases). Cette invariance découle du principe de Cavalieri : deux solides ont le même volume si, pour toute coupe parallèle aux bases, les sections ont la même aire.

Paramétrisation et équations

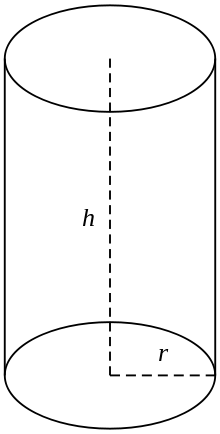
Un cylindre circulaire droit centré sur l'axe z s'exprime par l'équation x² + y² = r², indépendante de z. Une paramétrisation usuelle est (x,y,z) = (r cos θ, r sin θ, z) avec θ ∈ [0,2π) et z variable. Plus généralement, un cylindre est l'ensemble des points r(t) + s v, où r(t) parcourt une courbe plane et v est un vecteur fixe non nul; la direction v donne l'axe des génératrices.

Variantes et nomenclature

Cylindre circulaire droit : base circulaire et génératrices perpendiculaires aux bases.
Cylindre oblique : bases parallèles mais génératrices inclinées par rapport aux bases.
Cylindre elliptique : base elliptique (équation x²/a² + y²/b² = 1).
Cylindres paraboliques ou hyperboliques : lorsque la courbe génératrice est respectivement une parabole ou une hyperbole; ces surfaces conservent la propriété d'être engendrées par des droites parallèles.
Cylindre infini : surface non bornée utilisée en géométrie différentielle ou en physique (modèles de symétrie).

Propriétés différentielles et métriques

La surface latérale d'un cylindre droit est développable, c'est‑à‑dire qu'on peut la dérouler sur un plan sans distorsion; sa courbure gaussienne est nulle. En revanche, la courbure moyenne n'est généralement pas nulle. Le cylindre est un exemple simple de surface réglée et sert d'exemple pédagogique en géométrie différentielle et en topologie.

Moments d'inertie et propriétés physiques

En mécanique, le cylindre solide et la coque cylindrique sont des géométries courantes. Pour un cylindre solide homogène de masse m et de rayon r tournant autour de son axe central, le moment d'inertie est I = (1/2) m r². Pour une fine couche cylindrique (coque mince) de masse m on obtient I = m r². Ces formules sont largement utilisées en génie mécanique et en dynamique des rotations.

Histoire et développement mathématique

La connaissance des volumes et des aires des cylindres remonte à l'Antiquité, où les praticiens et savants utilisaient ces solides pour la construction, le stockage et le calcul de capacités. Les mathématiciens grecs, notamment ceux de l'école d'Archimède, ont étudié les rapports de volumes et mis au point des méthodes de quadrature et de comparaisons qui préfigurent l'intégration moderne.

Applications et exemples concrets

Les cylindres sont omniprésents : tuyaux et conduites, réservoirs et bouteilles, axes de machines, pistons et tubes, tambours, boîtes de conserve. Leur symétrie facilite la résolution de problèmes physiques (écoulement, conduction thermique, vibrations) et les rend favorables pour les calculs d'ingénierie et la fabrication industrielle.

Calculs pratiques

Pour vérifier la quantité de matière à remplir un réservoir cylindrique : V = π r² h.
Pour dimensionner une paroi cylindrique mince, on utilise l'aire latérale A_lat = 2 π r h pour évaluer la surface à couvrir et la résistance aux contraintes de membrane.
En fabrication, le déroulé d'une feuille métallique pour former un cylindre utilise la longueur 2πr et la hauteur h.

Utilisation commune

Dans l'usage courant, un cylindre est considéré comme une section finie d'un cylindre circulaire droit, c'est-à-dire le cylindre dont les génératrices sont perpendiculaires aux bases, avec ses extrémités fermées pour former deux surfaces circulaires, comme dans la figure (à droite). Si le cylindre a un rayon $r$ et une longueur (hauteur) h, alors son volume est donné par :

$V$ $= πr2h$

et sa surface est :

la zone du haut $(πr2) +$
la zone du fond $(πr2) +$
la zone du côté $($ 2πrh).

Par conséquent, sans le haut ou le bas (zone latérale), la surface est :

$A$ $=$ 2πrh.

Avec le haut et le bas, la surface est :

$A$ $= 2πr2 + 2πrh = 2πr(r + h)$ .

Pour un volume donné, le cylindre ayant la plus petite surface a $h = 2r$ . Pour une surface donnée, le cylindre ayant le plus grand volume a $h = 2r, c'est-à-dire que$ le cylindre tient dans un cube (hauteur = diamètre).

Volume

Avoir un cylindre circulaire droit avec une hauteur $h$ unités et une base de rayon $r$ unités avec les axes de coordonnées choisis de sorte que l'origine soit au centre d'une base et que la hauteur soit mesurée le long de l'axe x positif. Une section plane à une distance de $x unités de l$ 'origine a une surface de $A (x) unités$ carrées où

A ( x ) = π r 2 {\displaystyle A(x)=\pi r^{2}} $A(x)=\pi r^{2}$

A ( y ) = π r 2 {\displaystyle A(y)=\pi r^{2}} $A(y)=\pi r^{2}$

Un élément de volume, est un cylindre droit de surface de base $Awi$ unités carrées et une épaisseur de $Δix$ unités. Ainsi, si V unités cubiques est le volume du cylindre circulaire droit, par Riemann fait la somme,

V o l u m e d e c y l i n d e r = lim | | Δ → 0 | | ∑ i = 1 n A ( w i ) Δ i x {\displaystyle \mathrm {Volume\;of\;cylinder} =\lim _{||\Delta \to 0||}\sum _{i=1}^{n}A(w_{i})\Delta _{i}x} $\mathrm {Volume\;of\;cylinder} =\lim _{||\Delta \to 0||}\sum _{i=1}^{n}A(w_{i})\Delta _{i}x$

= ∫ 0 h A ( y ) 2 d y {\displaystyle =\int _{0}^{h}A(y)^{2}\,dy} $=\int _{0}^{h}A(y)^{2}\,dy$

= ∫ 0 h π r 2 d y {\displaystyle =\int _{0}^{h}\pi r^{2}\,dy} $=\int _{0}^{h}\pi r^{2}\,dy$

= π r 2 h {\displaystyle =\pi \,r^{2}\,h\,} $=\pi \,r^{2}\,h\,$

En utilisant des coordonnées cylindriques, le volume peut être calculé par intégration sur

= ∫ 0 h ∫ 0 2 π ∫ 0 r s d s d ϕ d z {\displaystyle =\int _{0}^{h}\int _{0}^{2\pi }\int _{0}^{r}s\,\,ds\,d\phi \,dz} $=\int _{0}^{h}\int _{0}^{2\pi }\int _{0}^{r}s\,\,ds\,d\phi \,dz$

= π r 2 h {\displaystyle =\pi \,r^{2}\,h\,} $=\pi \,r^{2}\,h\,$

Section cylindrique

Les sections cylindriques sont les intersections des cylindres avec les plans. Pour un cylindre circulaire droit, il existe quatre possibilités. Un plan tangent au cylindre, rencontre le cylindre en une seule ligne droite. Déplacé parallèlement à lui-même, le plan soit ne coupe pas le cylindre, soit le coupe en deux lignes parallèles. Tous les autres plans coupent le cylindre en une ellipse ou, lorsqu'ils sont perpendiculaires à l'axe du cylindre, en un cercle.

Autres types de cylindres

Un cylindre elliptique, ou cylindroïde, est une surface quadrique, dont l'équation suivante est en coordonnées cartésiennes :

( x a ) 2 + ( y b ) 2 = 1. $\left({\frac {x}{a}}\right)^{2}+\left({\frac {y}{b}}\right)^{2}=1.$

Cette équation concerne un cylindre elliptique, une généralisation du cylindre circulaire ordinaire ( $a = b$ ). Le cylindre généralisé est encore plus général : la section transversale peut être n'importe quelle courbe.

Le cylindre est un quadrique dégénéré car au moins une des coordonnées (dans ce cas $z$ ) n'apparaît pas dans l'équation.

Un cylindre oblique a les surfaces supérieure et inférieure décalées l'une par rapport à l'autre.

Il existe d'autres types de cylindres plus inhabituels. Ce sont les cylindres elliptiques imaginaires :

( x a ) 2 + ( y b ) 2 = - 1 {\displaystyle \left({\frac {x}{a}}\right)^{2}+\left({\frac {y}{b}}\right)^{2}=-1} $\left({\frac {x}{a}}\right)^{2}+\left({\frac {y}{b}}\right)^{2}=-1$

le cylindre hyperbolique :

( x a ) 2 - ( y b ) 2 = 1 {\displaystyle \left({\frac {x}{a}}\right)^{2}-\left({\frac {y}{b}}\right)^{2}=1} $\left({\frac {x}{a}}\right)^{2}-\left({\frac {y}{b}}\right)^{2}=1$

et le cylindre parabolique :

x 2 + 2 a y = 0. $x^{2}+2ay=0.\,$

Géométrie projective

En géométrie projective, un cylindre est simplement un cône dont le sommet est à l'infini.

Ceci est utile pour la définition des coniques dégénérées, qui nécessitent de considérer les coniques cylindriques.

Questions et réponses

Q : Qu'est-ce qu'un cylindre ?

R : Un cylindre est une forme géométrique tridimensionnelle dont la surface est formée par des points situés à une distance fixe d'un segment de ligne donné, appelé l'axe du cylindre. On peut le considérer comme un prisme circulaire et on peut appeler cylindre aussi bien la surface que la forme solide créée à l'intérieur.

Q : Depuis combien de temps les gens connaissent-ils la surface et le volume des cylindres ?

R : L'aire de surface et le volume des cylindres sont connus depuis l'Antiquité.

Q : Que sont les cylindres elliptiques, paraboliques et hyperboliques ?

R : Les cylindres elliptiques, paraboliques et hyperboliques sont des cylindres dont la section transversale est respectivement une ellipse, une parabole ou une hyperbole.

Q : Comment un cylindre est-il défini en géométrie différentielle ?

R : En géométrie différentielle, un cylindre est défini plus largement comme une surface réglée qui est couverte par une famille de lignes parallèles à un paramètre.

Q : Qu'est-ce que cela signifie pour quelque chose d'être "régi" ?

R : "Réglé" signifie que des lignes droites y sont tracées d'une manière ou d'une autre.

Q : N'y a-t-il qu'un seul type de cylindre ?

R : Non, il existe de nombreux types de cylindres différents tels que les cylindres elliptiques, paraboliques et hyperboliques qui ont tous des sections transversales différentes.

Auteur

AlegsaOnline.com - Cylindre - Leandro Alegsa

Date de création: 9 mai 2021
Dernière mise à jour: 20 avril 2026

URL: https://fr.alegsaonline.com/art/24894