Corrélation (statistiques)
En statistique et en théorie des probabilités, la corrélation signifie le degré d'interdépendance entre deux ensembles de données.
La corrélation ne signifie pas toujours que l'un provoque l'autre. Il est très possible qu'un troisième facteur soit en cause.
La corrélation a généralement deux directions. Elles sont positives ou négatives. Si elle est positive, alors les deux ensembles montent ensemble. Si elle est négative, alors l'une monte tandis que l'autre descend.
De nombreuses mesures de corrélation différentes sont utilisées pour différentes situations. Par exemple, sur un diagramme de dispersion, les gens tracent une ligne de meilleure concordance pour montrer la direction de la corrélation.
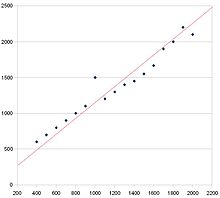
Ce diagramme de dispersion a une corrélation positive. Vous pouvez le dire parce que la tendance est à la hausse et à droite. La ligne rouge est une ligne de meilleur ajustement.
Explication de la corrélation
Fort et faible sont les mots utilisés pour décrire la corrélation. S'il y a une forte corrélation, alors les points sont tous proches les uns des autres. S'il y a une faible corrélation, alors les points sont tous éloignés les uns des autres. Il existe des moyens de faire en sorte que les chiffres montrent la force de la corrélation. Ces mesures sont appelées coefficients de corrélation. Le plus connu est le coefficient de corrélation produit-moment de Pearson. Vous introduisez des données dans une formule et cela vous donne un nombre. Si le nombre est 1 ou -1, alors il y a une forte corrélation. Si la réponse est 0, alors il n'y a pas de corrélation. Un autre type de coefficient de corrélation est le coefficient de corrélation de rang de Spearman.
Corrélation et causalité
La corrélation ne signifie pas toujours qu'une chose provoque l'autre (causalité), car une autre chose aurait pu provoquer les deux. Par exemple, les jours de grande chaleur, les gens achètent des glaces et vont aussi à la plage où certaines sont mangées par les requins. Il existe une corrélation entre la vente de glaces et les attaques de requins (dans ce cas, les deux augmentent avec la hausse de la température). Mais ce n'est pas parce que les ventes de glaces augmentent que les ventes de glaces provoquent (causent) plus d'attaques de requins ou vice versa.
Parce que la corrélation n'implique pas de causalité, les scientifiques, les économistes, etc. vont tester leurs théories en créant des environnements isolés où un seul facteur est modifié (lorsque cela est possible). Cependant, les hommes politiques, les vendeurs, les médias et d'autres personnes suggèrent souvent qu'une corrélation particulière implique une causalité. Cela peut être dû à l'ignorance ou à un désir de persuasion. Ainsi, un reportage peut attirer l'attention en disant que les personnes qui consomment un produit particulier ont plus souvent un problème de santé particulier, ce qui implique un lien de causalité qui pourrait en fait être dû à autre chose.
Pages connexes
- Cohen, J., Cohen P., West, S.G., & Aiken, L.S. (2003). Analyse de régression/corrélation multiple appliquée aux sciences du comportement. (3e éd.) Hillsdale, NJ : Lawrence Erlbaum Associates.
Questions et réponses
Q : Qu'est-ce que la corrélation ?
R : La corrélation est un moyen d'indiquer dans quelle mesure deux ensembles de données sont étroitement liés.
Q : La corrélation signifie-t-elle qu'un ensemble de données est à l'origine de l'autre ?
R : Non, la corrélation ne signifie pas toujours qu'un ensemble de données est à l'origine de l'autre. En fait, un troisième facteur intervient souvent.
Q : Quels sont les deux sens de la corrélation ?
R : Les deux sens de la corrélation sont positif et négatif.
Q : Que signifie une corrélation positive ?
R : Une corrélation positive signifie que les deux ensembles de données augmentent ensemble.
Q : Que signifie une corrélation négative ?
R : Une corrélation négative signifie qu'un ensemble de données augmente tandis que l'autre diminue.
Q : Existe-t-il différentes mesures de la corrélation ?
R : Oui, de nombreuses mesures différentes de la corrélation sont utilisées dans différentes situations.
Q : Comment indique-t-on souvent le sens de la corrélation sur un graphique de dispersion ?
R : On trace souvent une ligne de meilleur ajustement pour montrer le sens de la corrélation sur un graphique de dispersion.
Rechercher dans l'encyclopédie