Vecteur euclidien

Exemples de vecteurs

• John marche vers le nord sur 20 mètres. La direction "nord" ainsi que la distance "20 mètres" sont un vecteur.
• Une pomme tombe à 10 mètres par seconde. La direction "vers le bas" combinée à la vitesse "10 mètres par seconde" est un vecteur. Ce type de vecteur est également appelé vitesse.

Exemples de scalaires

• La distance entre deux endroits est de 10 kilomètres. Cette distance n'est pas un vecteur car elle ne contient pas de direction.
• Le nombre de fruits dans une boîte n'est pas un vecteur.
• Une personne qui pointe n'est pas un vecteur car il n'y a qu'une direction. Il n'y a pas de grandeur (la distance entre le doigt de la personne et un bâtiment, par exemple).
• La longueur d'un objet.
• Une voiture roule à 100 kilomètres à l'heure. Cela ne décrit pas un vecteur, car il n'y a qu'une magnitude, mais pas de direction.

Plus d'exemples de vecteurs

• Le déplacement est un vecteur. Le déplacement est la distance à laquelle une chose se déplace dans une certaine direction. Une mesure de la distance seule est un scalaire.
• La force qui inclut la direction est un vecteur.
• La vitesse est un vecteur, car elle est une vitesse dans une certaine direction.
• L'accélération est le taux de changement de la vitesse. Un objet accélère s'il change de vitesse ou de direction.

Comment ajouter des vecteurs

Ajout de vecteurs sur le papier selon la méthode de la tête à la queue

La méthode Head to Tail d'ajout de vecteurs est utile pour faire une estimation sur papier du résultat de l'ajout de deux vecteurs. Pour cela, il faut

• Chaque vecteur est dessiné comme une flèche avec une certaine longueur derrière elle, où chaque unité de longueur sur le papier représente une certaine grandeur du vecteur.
• Dessinez le vecteur suivant, avec la queue du second vecteur à la tête du premier vecteur.
• Répétez l'opération pour tous les autres vecteurs : Dessinez la queue du vecteur suivant en tête du vecteur précédent.
• Tracez une ligne de la queue du premier vecteur à la tête du dernier vecteur - c'est la résultante (somme) de tous les vecteurs.

On l'appelle la méthode "Head to Tail", car chaque tête du vecteur précédent mène à la queue du suivant.

Utilisation du formulaire des composants

^{[doit être expliqué]}

Utiliser la forme des composantes pour ajouter deux vecteurs signifie littéralement ajouter les composantes des vecteurs pour créer un nouveau vecteur. Par exemple, supposons que a et b soient deux vecteurs bidimensionnels. Ces vecteurs peuvent être écrits en fonction de leurs composantes.

a = ( a x , a y ) {\displaystyle \mathbf {a} =(a_{x},a_{y})}

b = ( b x , b y ) {\displaystyle \mathbf {b} =(b_{x},b_{y})}

Supposons que c soit la somme de ces deux vecteurs, de sorte que c = a + b. Cela signifie que c = ( a x + b x , a y + b y ) .

Voici un exemple d'addition de deux vecteurs, en utilisant leurs formes composantes.

a = ( 3 , - 1 ) {\displaystyle \mathbf {a} =(3,-1)}

b = ( 2 , 2 ) {\displaystyle \mathbf {b} =(2,2)}

c = a + b {\displaystyle \mathbf {c} =\mathbf {a} +\mathbf {b} }

= ( a x + b x , a y + b y )

= ( 3 + 2 , - 1 + 2 ) {\style d'affichage =(3+2,-1+2)}

= ( 5 , 1 ) {\displaystyle =(5,1)}

Cette méthode fonctionne pour tous les vecteurs, et pas seulement pour les vecteurs bidimensionnels.

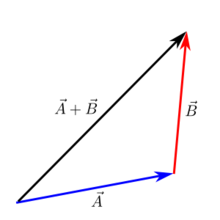
Ajout de la tête à la queue

Comment multiplier les vecteurs

Utilisation du produit point

Le produit scalaire est une méthode permettant de multiplier les vecteurs. Il produit un scalaire. Il utilise la forme des composants :

a = ( 2 , 3 ) b = ( 1 , 4 ) a ⋅ b = ( 2 , 3 ) ⋅ ( 1 , 4 ) = ( 2 ⋅ 1 ) + ( 3 ⋅ 4 ) = 2 + 12 = 14 {\displaystyle {\begin{aligned}\mathbf {a} =(2,3)\\\\mathbf {b} =(1,4)\\\\mathbf {a} \cdot \mathbf {b} =(2,3)\cdot (1,4)\\=(2\cdot 1)+(3\cdot 4)\\=2+12=14\end{aligné}}}}

Utilisation du produit croisé

Le produit croisé est une autre méthode pour multiplier les vecteurs. Il produit un autre vecteur. En utilisant la forme des composantes :

a × b = | a | | b | sin ( θ ) n {\displaystyle \mathbf {a} \times \mathbf {b} =|\mathbf {a} ||\mathbf {b} |\sin(\theta )\mathbf {n} }

Ici | a | {\displaystyle |\mathbf {a} |} signifie la longueur d'un affichage } et n {\displaystyle \mathbf {n} est le vecteur unitaire à angle droit d'un affichage de type \mathbf {a} } et b {\displaystyle \mathbf {b} } .

Multiplication par un scalaire

Pour multiplier un vecteur par un scalaire (un nombre normal), vous multipliez le nombre par chaque composante du vecteur :

c x = ( c x 1 , c x 2 , . . . , c x n ) {\displaystyle c\,\mathbf {x} =(c\,x_{1},c\,x_{2},... ,c\,x_{n})}

En voici un exemple

c = 5 x = ( 3 , 4 ) c x = ( 5 ⋅ 3 , 5 ⋅ 4 ) = ( 15 , 20 ) {\displaystyle {\begin{aligned}c=5\\\\\\mathbf {x} =(3,4)\c\,\mathbf {x} =(5\cdot 3,5\cdot 4)\\\=(15,20)\end{aligned}}}

Pages connexes

• Graphiques vectoriels
• Champ vectoriel