Cercle unité
En mathématiques, un cercle unitaire est un cercle de rayon 1. L'équation du cercle unitaire est x 2 + y 2 = 1 {\displaystyle x^{2}+y^{2}=1}
. Le cercle unitaire est centré à l'Origine, ou coordonnées (0,0). Il est souvent utilisé en Trigonométrie.
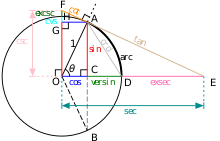
Le Unit Circle peut être utilisé pour modéliser chaque fonction trigonométrique.
Fonctions trigonométriques dans le cercle des unités
Dans un cercle unitaire, où t est l'angle souhaité, x
et y
peuvent être définis comme cos ( t
) = x
et sin ( t ) = y
. En utilisant la fonction du cercle d'unités, x 2 + y 2 = 1 on trouve une autre équation pour le cercle unitaire, cos 2 ( t ) + sin 2 ( t ) = 1 {\displaystyle \cos ^{2}(t)+\sin ^{2}(t)=1}
. Lorsque l'on travaille avec des fonctions trigonométriques, il est surtout utile d'utiliser des angles dont les mesures sont comprises entre 0 et π 2 {\displaystyle \pi \over 2}
radians, ou 0 à 90 degrés. Il est toutefois possible d'avoir des angles plus élevés. En utilisant le cercle unitaire, deux identités peuvent être trouvées : cos ( t ) = cos ( 2 ⋅ π k + t ) {\displaystyle \cos(t)=\cos(2\cdot \pi k+t)}
et s i n ( t ) = sin ( 2 ⋅ π k + t ) {\displaystyle sin(t)=\sin(2\cdot \pi k+t)}
pour tout entier k {\displaystyle k}
.
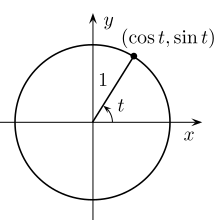
Le cercle unitaire peut substituer des variables aux fonctions trigonométriques.
Questions et réponses
Q : Qu'est-ce qu'un cercle unité ?
R : Un cercle unitaire est un cercle dont le rayon est égal à 1.
Q : Quelle est l'équation du cercle unité ?
R : L'équation du cercle unitaire est x^2 + y^2 = 1.
Q : Où est centré le cercle unitaire ?
R : Le cercle unitaire est centré sur l'Origine, ou sur les coordonnées (0,0).
Q : Quelle est l'utilité du cercle unitaire en mathématiques ?
R : Le cercle unité est souvent utilisé en trigonométrie.
Q : Pourquoi le cercle des unités est-il important ?
R : Le cercle des unités est important car il aide à comprendre les relations entre les angles et les fonctions trigonométriques.
Q : Quel est le rayon du cercle unitaire ?
R : Le rayon du cercle unitaire est égal à 1.
Q : Que signifie le fait que le rayon du cercle unitaire soit égal à 1 ?
R : Le fait que le rayon du cercle unitaire soit égal à 1 simplifie les calculs et permet de relier facilement les angles aux valeurs trigonométriques.
