Principe d'incertitude

Diagrammes

1. Les photons, électrons et autres particules subatomiques se focalisent lorsqu'ils sont tirés à travers un grand trou, mais nous ne savons pas exactement où ils se trouvaient à mi-chemin.


2. En rétrécissant le trou, les trajectoires des particules se courbent autour des bords du trou (diffraction), de sorte que le faisceau résultant devient plus grand et plus doux.


3. Le rétrécissement du trou augmente la certitude de savoir où se trouve le photon au milieu, mais sa direction de là vers l'écran de détection de droite devient alors plus incertaine. La mise au point devient floue. En élargissant le trou, les photons se retrouvent tous au centre de l'écran de détection, mais nous avons alors une moins bonne idée de l'endroit où ils se trouvaient lorsqu'ils ont traversé la barrière centrale.


4. Le montage de ressorts sur une barrière munie d'un petit trou fait que la particule passe à travers le trou, ce qui pousse la barrière, étire les ressorts et mesure ainsi l'élan. Mais comme la barrière montée sur ressort se déplace, nous sommes moins sûrs de l'endroit où se trouvait la particule lorsqu'elle est passée par le trou, et la diffraction affectera également sa position sur l'écran de détection.


5. La suspension de l'espace central par des échelles à ressort permet de mesurer l'élan, mais ce faisant, l'espace est déplacé de manière imprévisible, de sorte que les informations sur l'emplacement de chaque photon au milieu sont perdues.


6. Cette animation montre l'une des conséquences importantes de la nature incertaine de l'univers : le tunnelage quantique des électrons. Regardez bien. Chaque fois qu'un petit bout passe la barrière.

Comment les humains ont-ils appris l'incertitude ?

Très peu de temps après que Werner Heisenberg ait créé la nouvelle physique quantique, quelque chose d'inattendu est sorti tout droit de ses mathématiques, l'expression :

Δ x Δ p ≳ h 4 π {\displaystyle \Delta x\,\Delta p\gtrsim {\frac {h}{4\pi }}\qquad \qquad \qquad }

La plage d'erreur de position (x) multipliée par la plage d'erreur de moment (p) est à peu près égale ou supérieure à la constante de Planck divisée par 4π.

Ces symboles mettent sous forme mathématique ce que vous avez déjà vu dans les images ci-dessus. Les symboles indiquent clairement que vous ne pouvez pas être parfaitement certain de l'endroit où se trouve une chose et de sa destination. Si vous êtes plus clair sur l'endroit où il se trouve à un moment donné, vous avez moins d'idée sur sa destination et sa vitesse. Si vous savez plus clairement où elle va et à quelle vitesse à tout moment, vous avez moins d'idée de l'endroit où elle se trouve en ce moment.

Les scientifiques avaient déjà appris pourquoi certaines substances émettent des couleurs de lumière caractéristiques lorsqu'elles sont chauffées ou excitées. Heisenberg essayait d'expliquer pourquoi ces couleurs ont chacune une luminosité caractéristique. Cela n'aurait pas suffi si lui et les autres scientifiques avaient simplement dit : "Eh bien, c'est comme ça". Ils étaient sûrs qu'il devait y avoir une bonne raison à ces différences, et au fait que les rapports entre les intensités des lignes brillantes étaient toujours les mêmes pour chaque échantillon d'un élément.

Il n'avait aucune idée qu'il allait tomber sur un secret caché de la nature lorsqu'il est parti à la découverte de l'explication des intensités des lignes colorées caractéristiques de chacun des éléments. L'étude de la mécanique quantique avait déjà montré pourquoi l'hydrogène possède quatre raies brillantes dans la partie du spectre que les humains peuvent voir. Il a dû sembler que la prochaine chose à apprendre serait simplement de calculer leur luminosité. L'hydrogène semblait être le point de départ évident puisque l'hydrogène n'a qu'un seul électron à traiter, et seulement quatre raies dans la partie visible du spectre. Il doit sûrement y avoir une bonne raison pour qu'ils ne soient pas aussi brillants. L'explication de la luminosité des lignes de couleur différente du néon et des autres éléments pourrait attendre.

 

Heisenberg a commencé à travailler sur la physique quantique en adaptant les équations classiques pour l'électricité, qui sont très compliquées au départ, de sorte que les mathématiques qui se cachent derrière son article de 1925 étaient très difficiles à suivre.

Il essayait de trouver le bon moyen de calculer l'intensité des raies brillantes dans le spectre des lampes à hydrogène. Il a dû trouver une quantité connexe appelée "amplitude" et multiplier l'amplitude par l'amplitude (ou en d'autres termes, il a dû élever l'amplitude au carré) pour obtenir l'intensité qu'il voulait. Il a dû trouver comment exprimer l'amplitude d'une manière qui tienne compte du fait que les lampes à hydrogène ne rayonnent pas à toutes les fréquences, et ne rayonnent pas sur une gamme continue de fréquences dans la partie du spectre que les gens peuvent voir. Heisenberg a trouvé une nouvelle façon remarquable de calculer l'amplitude.

L'étrange équation que Heisenberg a découverte et utilisée pour multiplier une quantité quantique (par exemple, la position) par une autre (par exemple, le moment) a été publiée dans ce qu'on a appelé "l'article "magique" de Heisenberg de juillet 1925".

C ( n , n - b ) = ∑ a A ( n , n - a ) B ( n - a , n - b )

Le calcul ci-dessus semble très difficile, mais le calcul qui le précède est beaucoup plus difficile et est extrêmement difficile à comprendre. Il est donné ici juste pour montrer à quoi il ressemblait. L'article d'Heisenberg est un point de repère historique. De nombreux physiciens qui ont lu son article ont déclaré qu'ils ne pouvaient pas être en désaccord avec ses conclusions, mais qu'ils ne pouvaient pas suivre son explication sur la façon dont il est arrivé à ces conclusions. Les équations de départ utilisées par Heisenberg impliquaient des séries de Fourier, et faisaient intervenir de nombreux facteurs. Nous reviendrons sur l'équation ci-dessus car elle est une sorte de recette pour écrire et multiplier des matrices.

Les nouvelles équations devaient être si étranges et inhabituelles car Heisenberg décrivait un monde étrange dans lequel certaines choses, comme les orbites des électrons, ne deviennent pas lentement plus grandes ou plus petites. Les nouveaux types de changements impliquent des sauts et de grands écarts entre les sauts. Les électrons ne peuvent sauter qu'entre certaines orbites, et l'énergie gagnée ou perdue en changeant d'orbite est produite lorsqu'un photon de la bonne énergie est absorbé ou qu'un nouveau photon de la bonne énergie est produit. Si les électrons des atomes d'hydrogène sautent (tombent) le plus souvent entre deux orbites particulières, alors plus de photons seront émis à ce niveau d'énergie, et donc la lumière produite à ce niveau sera la plus intense.

Il était difficile de faire correspondre des équations construites pour des spectres continus (ce que vous voyez lorsque vous faites passer la lumière du soleil à travers un prisme) à des spectres qui n'ont que quelques fréquences de crête entre lesquelles il n'y a rien. Presque tout ce qui avait déjà été appris sur la lumière et l'énergie avait été fait avec de grandes choses comme des bougies allumées ou des soleils, et ces grands objets produisent tous des spectres continus. Même si ces objets de taille ordinaire sont faciles à expérimenter, il a fallu beaucoup de temps pour comprendre les lois (physiques) qui les régissent. Aujourd'hui, les physiciens s'occupent de choses trop petites pour être vues, de choses qui ne produisent pas de spectres continus, et essaient de trouver un moyen d'obtenir au moins des indices à partir de ce qu'ils savent déjà, afin de les aider à trouver les lois de ces petites sources de lumière.

Les équations initiales portaient sur une sorte de corps vibrant qui produirait une onde, un peu comme l'anche d'un organe produirait une onde sonore d'une fréquence caractéristique. Il y avait donc un mouvement de va-et-vient (comme la vibration d'une anche) et une onde émise qui pouvait être grapillée comme une onde sinusoïdale. Une grande partie de ce qui avait été découvert auparavant sur la physique au niveau atomique concernait les électrons qui se déplaçaient autour des noyaux. Lorsqu'une masse se déplace sur une orbite, lorsqu'elle tourne autour d'une sorte de moyeu, elle a ce que l'on appelle un "moment angulaire". Le moment angulaire est la façon dont quelque chose comme un manège continue à tourner après que les gens ont cessé de le pousser. Le calcul des phases et du moment angulaire est compliqué. De plus, Heisenberg n'a pas montré tous ses calculs dans son article de 1925, de sorte que même les bons mathématiciens pourraient avoir du mal à remplir ce qu'il n'a pas dit.

Même si de nombreux physiciens ont déclaré qu'ils ne pouvaient pas comprendre les différentes étapes mathématiques dans l'article de Heisenberg, un article récent qui tente d'expliquer comment Heisenberg a obtenu son résultat utilise vingt pages remplies de mathématiques. Même cet article n'est pas facile à comprendre. Les mathématiques ont commencé avec des choses vraiment difficiles et ont finalement produit quelque chose de relativement simple qui est montré en haut de cet article. Obtenir un résultat plus simple n'a pas été facile, et nous n'allons pas essayer de montrer le processus qui a permis de passer d'une image dépassée de l'univers à la nouvelle physique quantique. Nous avons juste besoin de suffisamment de détails pour montrer que, presque dès qu'Heisenberg a fait sa percée, une partie du fonctionnement de l'univers que personne n'avait jamais vue auparavant est apparue.

Heisenberg devait être très excité mais aussi très fatigué lorsque, tard dans la nuit, il a finalement réussi à percer et a commencé à se prouver que cela allait marcher. Presque tout de suite, il a remarqué quelque chose d'étrange, quelque chose qu'il pensait être un petit problème ennuyeux qu'il pouvait faire disparaître d'une manière ou d'une autre. Mais il s'est avéré que cette petite nuisance était une grande découverte.

Heisenberg avait travaillé à la multiplication des amplitudes par des amplitudes, et maintenant Heisenberg avait une bonne façon d'exprimer l'amplitude en utilisant sa nouvelle équation. Naturellement, il pensait à la multiplication, et à la façon dont il multiplierait les choses qui étaient données en termes d'équations compliquées.

Heisenberg s'est rendu compte qu'en plus d'élever l'amplitude au carré, il voudrait éventuellement multiplier la position par l'élan, ou multiplier l'énergie par le temps, et il semblait que cela ferait une différence s'il inversait l'ordre dans ces nouveaux cas. Heisenberg ne pensait pas qu'il fallait se soucier de savoir si une position était multipliée par l'élan ou si une position était multipliée par l'élan. S'il s'était agi de simples chiffres, il n'y aurait pas eu de problème. Mais il s'agissait dans les deux cas d'équations compliquées, et la façon dont vous avez fait entrer les chiffres dans les équations s'est avérée différente selon la façon dont vous avez commencé. Dans la nature, il fallait mesurer la position puis l'élan, ou alors il fallait mesurer l'élan puis la position, et en mathématiques, la même situation générale prévalait. (Voir l'article de Wikipedia en anglais "Heisenberg's entryway to matrix mechanics" si vous voulez apprendre les détails difficiles). Les différences minuscules mais gênantes entre les résultats allaient subsister, peu importe à quel point Heisenberg souhaitait qu'elles disparaissent.

À l'époque, Heisenberg ne pouvait pas se débarrasser de ce petit problème, mais il était épuisé, alors il a remis son travail à son supérieur direct, Max Born, et est parti en vacances.

Max Born était un mathématicien remarquable qui a vite vu que l'équation que lui avait donnée Heisenberg était une sorte de recette pour écrire une matrice. Le Dr. Born était l'une des rares personnes à l'époque à s'intéresser à ce genre de maths bizarres que la plupart des gens trouvaient peu utiles. Il savait que les matrices pouvaient être multipliées, et que tous les calculs nécessaires pour résoudre un problème de physique pouvaient être effectués en multipliant une matrice par une autre. Le simple fait de pouvoir mettre une procédure compliquée sous une forme standard et acceptable rendrait le travail plus facile. Cela pourrait également faciliter l'acceptation par d'autres personnes.

Born était un si bon mathématicien qu'il a presque immédiatement réalisé que le fait de changer l'ordre de multiplication des deux matrices produirait un résultat différent, et que les résultats différeraient d'une petite quantité. Ce montant serait h/2πi. Dans la vie de tous les jours, cette différence serait si faible que nous ne pourrions même pas la voir.

Lorsque certaines molécules sont excitées, elles dégagent une couleur caractéristique.


Spectre de l'hydrogène


Spectre néon


Spectre visuel complet du soleil. Il n'y a pas de lacunes. Ce graphique montre les intensités aux différentes fréquences.


Deux vagues déphasées l'une par rapport à l'autre

Vers une théorie formelle de l'incertitude

Cela a pris quelques années, mais Heisenberg a pu prouver le principe d'incertitude, qui dit que Δx × Δp = h/2, qui est le nombre qui ressort des équations initiales mais qui ne tient pas compte du π et du i qui ont trait aux changements de phase. Heisenberg a expliqué qu'il a dérivé son principe d'incertitude de ce résultat antérieur lorsqu'il a écrit un article en 1927 présentant cette théorie.

La constante écrite h, appelée constante de Planck, est un nombre mystérieux qui se produit souvent, nous devons donc comprendre ce qu'est ce petit nombre. Numériquement, il est généralement donné sous la forme 6,62607×10^-34 J s (joules secondes). Il s'agit donc d'une quantité qui implique de l'énergie et du temps.

Elle a été découverte lorsque Planck a réalisé que l'énergie d'un radiateur parfait (appelé radiateur à corps noir) est émise en unités de taille définie appelées "quanta" (le singulier de ce mot est "quantum"). L'énergie rayonnée est émise sous forme de photons, et la fréquence d'un photon est proportionnelle au "coup de poing" qu'il délivre. Nous expérimentons différentes fréquences de la lumière visible sous forme de différentes couleurs. À l'extrémité violette du spectre, chaque photon a une quantité d'énergie relativement importante ; à l'extrémité rouge du spectre, chaque photon a une quantité d'énergie relativement faible. La façon de calculer la quantité d'énergie d'un photon est donnée par l'équation E = hν (l'énergie est égale à la constante de Planck multipliée par "nu" ou fréquence).

Le principe d'incertitude d'Heisenberg Δx × Δp ≥ h nous dit que lorsque nous essayons de déterminer certaines paires de nombres, nous ne pouvons pas nous en approcher plus que cela, et que si nous essayons de clarifier l'une d'entre elles, c'est-à-dire si nous essayons de rendre Δx plus petit pour avoir une meilleure idée de la position de quelque chose, alors nous devrons obtenir un nombre plus grand pour l'autre nombre de la paire, et que la différence entre les deux est étroitement liée à h.

Une autre paire de grandeurs physiques se base sur la relation d'incertitude : ΔE × Δt ≥ h, et cette paire indique, entre autres, que si nous cherchons dans l'espace interstellaire, un endroit où nous ne nous attendrions pas à trouver quoi que ce soit, et que nous réduisons Δt de plus en plus près de 0, alors pour maintenir l'équilibre indiqué dans l'équation ΔE doit devenir de plus en plus grand - et soudain quelque chose avec un élan peut apparaître juste pour cette brève période de temps.

Comment expliquer cette indétermination (manque de certitude) ? Que se passe-t-il dans l'Univers ? On dit souvent qu'une nouvelle théorie qui réussit peut fournir de nouvelles informations sur les phénomènes étudiés. Heisenberg a créé un modèle mathématique qui a prédit les intensités correctes pour le spectre des raies brillantes de l'hydrogène, mais sans en avoir l'intention, il a découvert que certaines paires de quantités physiques révèlent une incertitude inattendue. Jusqu'à ce moment, personne ne savait que les mesures ne pourraient pas être éternellement plus précises et exactes. Le fait qu'elles ne puissent pas être rendues plus certaines, plus précises, a été une nouvelle découverte étonnante. Beaucoup de gens n'étaient pas prêts à l'accepter.

Bohr et ses collègues ont fait valoir que les photons, les électrons, etc. n'ont ni position ni élan tant qu'ils ne sont pas mesurés. Cette position théorique est née de la découverte de l'incertitude, et n'est pas seulement une préférence personnelle sur ce qu'il faut croire. Bohr a déclaré que nous ne savons rien sur quelque chose comme un photon ou un électron tant que nous ne l'avons pas observé. Pour observer une chose aussi petite, nous devons interagir avec elle d'une manière ou d'une autre. Dans la vie quotidienne, il est possible de faire quelque chose comme marcher à côté d'une voiture tout en notant les moments où elle passe des points sur une grille tracée sur le trottoir. Peut-être le poids de l'automobile lui-même vient-il appuyer sur de petits leviers situés sur le trottoir qui éteignent les horloges fixées à chacun d'eux et enregistrent le poids de l'automobile. En fin de compte, nous aurions un enregistrement clair de l'endroit où se trouvait la voiture à différents moments, et nous pourrions également calculer sa direction de progression et son poids. Nous pourrions alors connaître, à tout moment sur l'horloge, à la fois sa position et son élan (sa vitesse multipliée par sa masse). Nous n'imaginerions même pas que la force nécessaire pour déplacer les petits leviers ait une quelconque influence sur la progression de la voiture. Nous n'imaginerions pas non plus que l'automobile n'ait pas d'emplacement ou de trajectoire entre les points du trottoir où se trouvent les leviers, ou que la voiture existe dans une sorte de flou tridimensionnel à ces moments-là et ne s'immobilise que lorsqu'elle appuie sur un levier. Le monde qui nous est familier ne révèle pas ces étranges types d'interactions.

Pour localiser un navire sur la mer pendant la nuit la plus sombre, nous pourrions utiliser un projecteur, et cette lumière ne perturberait pas la position ou la direction de déplacement du navire, mais pour localiser un électron avec de la lumière, il faudrait le frapper avec un ou plusieurs photons ayant chacun un élan suffisant pour perturber la position et la trajectoire de l'électron. Pour localiser l'électron par d'autres moyens, il faudrait le maintenir dans une sorte de contrainte physique qui mettrait également fin à son mouvement vers l'avant.

Pour localiser un photon, le mieux que l'on puisse faire sans interrompre son mouvement vers l'avant est de lui faire traverser un trou circulaire dans une barrière. Si l'on connaît l'heure à laquelle le photon a été émis (par un laser, par exemple) et l'heure à laquelle le photon arrive à un écran de détection tel qu'un appareil photo numérique, il est alors possible de calculer le temps nécessaire pour parcourir cette distance et l'heure à laquelle le photon a traversé le trou. Cependant, pour permettre au photon de passer à travers, le trou circulaire doit avoir un diamètre supérieur à la taille du photon. Plus le trou circulaire est petit, plus on est proche de connaître la position exacte du photon lorsqu'il le traverse. Cependant, nous ne pouvons jamais savoir si le photon est décentré à ce moment-là. Si le trou est exactement de la même taille que le photon, il ne passera pas à travers. À mesure que le diamètre du trou diminue, l'impulsion ou la direction du photon à sa sortie du trou est de plus en plus modifiée.

Niels Bohr et ses collègues ont fait valoir que nous nous attirons de gros ennuis si nous supposons que ce qui est vrai est trop petit pour être vu, même au microscope, ce dont nous n'avons la preuve qu'à l'échelle de la vie quotidienne. Dans la vie quotidienne, les choses ont une position définie à tout moment. À l'échelle atomique, nous n'avons aucune preuve pour étayer cette conclusion. Dans la vie de tous les jours, les choses ont un moment précis où elles se produisent. À l'échelle atomique, nous n'avons aucune preuve pour étayer cette conclusion. Dans la vie de tous les jours, si l'on observe une usine du quart de nuit du premier jour au quart de jour du deuxième jour et que l'on voit une automobile terminée rouler jusqu'au quai d'expédition, il serait insensé de dire qu'il est impossible de dire si elle a été livrée pendant le quart de nuit ou pendant le quart de jour. Mais à l'échelle atomique, on peut montrer des cas où il faut compter un seul photon comme ayant été produit à deux reprises. (Si cela n'est pas suffisant, nous pouvons également montrer des cas où un seul photon est produit par deux lasers adjacents).

Une partie de la difficulté pour savoir ce qui se passe à l'échelle atomique est que nous voudrions savoir à la fois où se trouve une chose et quelle est sa trajectoire, et connaître les deux choses en même temps, mais nous ne pouvons pas mesurer à la fois la position et la trajectoire. Soit nous mesurons l'impulsion d'un photon ou d'un électron à un moment donné et ensuite, sans plus de retard que nécessaire, nous mesurons sa position, soit nous inversons les choses et nous mesurons d'abord la position et ensuite l'impulsion. Le problème est qu'en donnant au premier une forme assez précise (en le pressant d'une certaine manière), nous augmentons l'incertitude de la mesure suivante. Si nos mesures initiales étaient si grossières que beaucoup d'erreurs étaient introduites dans chacune d'elles, nous pourrions améliorer les choses en utilisant une touche plus légère pour chacune d'elles, mais nous ne pourrions jamais dépasser une certaine limite de précision.

Nous savons par la vie quotidienne qu'en essayant de peser quelque chose sur un pèse-personne placé sur un lave-linge en cycle d'essorage, on obtient des résultats inexacts parce que l'aiguille du pèse-personne bouge beaucoup. Nous pouvons éteindre la machine à laver. Mais pour des mesures très précises, nous constatons que les camions qui passent dans le quartier font bouger l'aiguille, de sorte que nous pouvons placer le pèse-personne sur un objet pour l'isoler des perturbations extérieures. Nous pensons que nous pouvons éliminer suffisamment de vibrations pour obtenir des résultats aussi précis que nous le souhaitons. Nous ne considérons jamais que la chose sur la balance est elle-même vibrante ou qu'elle possède un élan indéfini.

Si l'on se réfère au principe d'incertitude, il semble qu'il n'y ait en fait aucune position définie et aucun élan défini pour toute chose à l'échelle atomique, et que les expérimentateurs ne peuvent forcer les choses à être définies que dans les limites fixées par le principe d'incertitude. Bohr et ses collègues ont seulement fait valoir que nous ne pouvions rien savoir sans effectuer de mesures, et que lorsque des mesures ont été effectuées, nous pouvons pousser les choses dans le sens d'une position plus définie ou d'un élan plus défini, mais que nous ne pouvons pas obtenir la certitude ou la définition absolue que nous souhaiterions. Mais d'autres ont pris cette possibilité au sérieux, et ont fait valoir que si les calculs sont justes, il ne peut y avoir de définition ou de certitude dans le monde de l'ultra petit. La nature de la science est que les mathématiques ne sont qu'un modèle de la réalité, et il n'y a aucune garantie qu'il s'agisse d'un modèle correct.

Les mathématiques et les conséquences pratiques des choses qu'elles prédisent sont si fiables qu'il est très difficile de ne pas être d'accord avec elles, mais ce que les mathématiques disent sur le monde réel a produit plusieurs idées différentes. Parmi les scientifiques qui ont travaillé avec Niels Bohr à Copenhague, le principe d'incertitude a été pris pour signifier qu'à un niveau élémentaire, l'univers physique n'existe pas sous une forme déterministe. Il s'agit plutôt d'un ensemble de probabilités ou de potentiels.

Contrairement à l'histoire tissée autour des mathématiques par le groupe de Copenhague, il y a d'autres histoires comme celle de "l'interprétation des univers multiples" qui dit que chaque fois qu'il y a plusieurs résultats possibles selon la théorie quantique, chaque résultat se produit dans son propre nouvel univers. Einstein a soutenu qu'il n'y a pas de multiples résultats possibles, donc il n'y a qu'un seul univers et il est déterminé, ou, comme il l'a dit, "Dieu ne joue pas aux dés".

Si h était la plus petite quantité d'énergie possible, alors l'équation de base montrant l'énergie contenue dans les photons de différentes fréquences ne serait pas équilibrée. Elle serait fausse.

Objections contre le principe d'incertitude

Albert Einstein a vu que la nouvelle mécanique quantique impliquait un manque de position et d'élan dans le temps précédant la réalisation des mesures, et il s'y est opposé avec force. Il croyait fermement que les choses avaient des positions et des moments précis avant d'être mesurées, et que le fait de mesurer l'une des deux choses et de perturber la possibilité de mesurer l'autre avec précision ne plaide pas en faveur d'un manque de l'une ou l'autre au préalable. Lui et deux de ses collègues ont écrit ce qui est connu sous le nom de "EPR paper". Ce document soutient qu'il doit y avoir des caractéristiques qui déterminent la position et l'élan, et que si nous pouvions les voir, ou si nous pouvions obtenir des informations à leur sujet, alors nous pourrions mathématiquement connaître et prédire la position et l'élan. Pendant longtemps, les gens ont pensé qu'il n'y avait aucun moyen de prouver ou de réfuter ce qui était pour Einstein un article de foi. L'argument a été très productif car il a conduit à tous les développements modernes en matière d'enchevêtrement.

Mathématiquement, il a été prouvé qu'Einstein avait tort. En 1964, John Stewart Bell a développé une méthode mathématique pour distinguer le comportement de deux particules qui ont des états déterminés simplement inconnus des deux individus qui les étudient, et deux particules qui ont des états enchevêtrés qui sont indéterminés ou incertains jusqu'à ce qu'ils soient mesurés. Sa méthode montre que les probabilités d'obtenir certains résultats sont différentes selon les deux hypothèses. Son travail est appelé théorème de Bell ou inégalité de Bell. Les expériences ont montré que la nature se comporte comme Bell le décrit.

Une autre voie vers l'incertitude

Les premières discussions sur le principe d'incertitude de Heisenberg reposaient sur un modèle qui ne tenait pas compte du fait que les particules de matière telles que les électrons, les protons, etc. ont une longueur d'onde. En 1926, Louis de Broglie a montré que toutes les choses, et pas seulement les photons, ont leur propre fréquence. Les choses ont une nature ondulatoire et une nature particulaire, tout comme les photons. Si nous essayons de rendre l'onde d'une chose comme un proton plus étroite et plus haute, cela rendrait sa position plus claire, mais alors l'élan serait moins bien défini. Si nous essayons de rendre plus claire la partie de l'impulsion d'une description d'onde, c'est-à-dire de la faire rester dans une plage de valeurs plus étroite, alors le pic de l'onde s'étale et sa position devient moins définie.

L'onde qui fait partie de la description d'un photon n'est pas, en mécanique quantique, le même genre de chose qu'une onde à la surface de l'océan ou que les régions d'air comprimé et d'air raréfié qui composent les ondes sonores. Au contraire, ces ondes ont des pics ou des régions de grande amplitude qui ont à voir avec la probabilité de trouver quelque chose à ce point dans l'espace et le temps. Plus précisément, c'est le carré de l'amplitude qui donne la probabilité de voir apparaître un phénomène.

L'onde qui s'applique à un photon pourrait être une onde sinusoïdale pure. Dans ce cas, le carré de la valeur de chaque pic donnerait la probabilité d'observer le photon en ce point. Comme les amplitudes des ondes sinusoïdales sont partout les mêmes, la probabilité de trouver le photon à chacun d'eux serait la même. Donc, en pratique, connaître l'onde d'un de ces photons ne donnerait aucune indication sur l'endroit où le chercher. D'autre part, la quantité de mouvement d'un photon est mathématiquement liée à l'amplitude de son onde. Puisque dans ce cas nous avons une onde sinusoïdale pure, l'amplitude de chaque cycle de l'onde est la même et donc il n'y a qu'une seule valeur d'impulsion associée à cette onde. Nous ne saurions pas où le photon frapperait, mais nous saurions exactement avec quelle force il frapperait.

Dans les faisceaux de lumière qui se concentrent sur un point quelconque d'un écran de détection, les ondes associées aux photons ne sont pas de pures ondes sinusoïdales. Il s'agit plutôt d'ondes de forte amplitude en un point et d'amplitudes beaucoup plus faibles de part et d'autre de ce pic le plus élevé. Mathématiquement, il est possible d'analyser une telle onde en un certain nombre d'ondes sinusoïdales de différentes longueurs d'onde. Il est un peu plus facile de visualiser l'inverse de ce processus en regardant une première onde sinusoïdale d'une fréquence à laquelle s'ajoute une deuxième onde sinusoïdale d'une longueur d'onde différente, puis une troisième, puis une quatrième, et ainsi de suite. Le résultat sera une onde complexe présentant un pic élevé et contenant un grand nombre d'ondes de différentes longueurs d'onde et donc de différents moments. Dans ce cas, la probabilité que le photon apparaisse à un certain moment est extrêmement élevée, mais le moment qu'il délivre peut s'avérer être lié à la longueur d'onde de l'une des ondes composantes. En d'autres termes, la valeur de p = ħ/λ n'est plus une valeur unique car toutes les longueurs des "ondes de longueur d'onde différentes" assemblées doivent être prises en compte.

La simulation montre comment modéliser mathématiquement l'affinement de l'emplacement d'une particule : Superposer de nombreuses formes d'ondes différentes sur l'onde sinusoïdale d'origine. Le centre formera un pic de plus en plus élevé, et les autres pics seront plus nombreux mais moins hauts car ils interféreront les uns avec les autres. Au final, il y a donc de nombreuses ondes différentes dans la superposition, chacune avec une longueur d'onde différente et (par p = λ/λ) un élan différent, mais un seul pic très élevé, qui devient de plus en plus haut et étroit et nous donne quelque chose de plus en plus proche d'une position déterminée.

Pour rendre l'élan de plus en plus net, il faudrait enlever de plus en plus d'ondes sinusoïdales superposées jusqu'à ce qu'il ne reste plus qu'une simple onde sinusoïdale. Ce faisant, nous diminuerions progressivement la hauteur du pic central et augmenterions progressivement les hauteurs des endroits concurrents où l'on pourrait trouver la particule.

Ainsi, lorsque nous commençons avec une image d'onde de particules subatomiques, nous traitons toujours des cas avec des pics centraux relativement élevés et des longueurs d'onde de composants relativement nombreuses. Il n'y aura jamais de position exacte ou de moment précis prévu dans ces circonstances. Si le modèle mathématique est une représentation exacte du monde réel, alors aucun photon ou autre particule subatomique n'a de position exacte ou de moment défini. Lorsque nous mesurons une telle particule, nous pouvons choisir une méthode qui comprime davantage le pic et le rend plus étroit, ou nous pouvons choisir une méthode qui abaisse le pic et égalise les longueurs d'onde des composants. En fonction de ce que nous mesurons et de la manière dont nous le mesurons, nous pouvons rendre notre position plus précise ou nous pouvons réduire la gamme de notre impulsion. Nous pouvons prendre soin, lors de la conception de l'expérience, d'éviter les différentes façons de secouer l'appareil, mais nous ne pouvons pas nous débarrasser du fait qu'il n'y avait rien de complètement défini au départ.

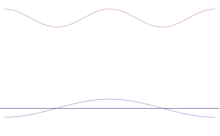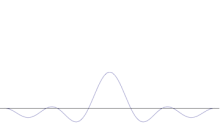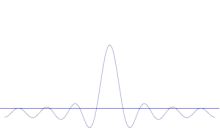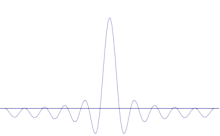
La superposition de plusieurs ondes planes. Le paquet d'ondes devient de plus en plus localisé avec l'ajout de nombreuses ondes. La transformée de Fourier est une opération mathématique qui sépare un paquet d'ondes en ses ondes planes individuelles. Notez que les ondes présentées ici sont réelles à titre d'illustration uniquement, alors qu'en mécanique quantique, la fonction d'onde est généralement complexe.

Les influences culturelles

L'influence la plus importante du principe d'incertitude de Heisenberg s'est exercée sur les arguments relatifs à la liberté du testament. Selon les théories de la physique classique, il est possible d'affirmer que les lois de cause à effet sont inexorables et qu'une fois que l'univers a commencé d'une certaine manière, les interactions de toute la matière et de l'énergie qui se produiront dans le futur pourraient être calculées à partir de cet état initial. Comme tout est absolument le résultat de ce qui l'a précédé, on a fait valoir que chaque décision qu'un être humain prend et chaque situation dans laquelle il entre est prédéterminée depuis le début des temps. Nous n'avons donc pas le choix de ce que nous faisons.

Les personnes qui croient en la liberté de la volonté affirment que les lois de la mécanique quantique ne prédisent pas ce qui va se passer, mais seulement ce qui est plus ou moins susceptible de se produire. Par conséquent, chaque action est le résultat d'une série de "tirages au sort" aléatoires et aucune décision ne peut être attribuée à un ensemble de conditions préalables nécessaires.

Les expressions "saut quantique" et "saut de géant" sont devenues des façons ordinaires de parler des choses. En général, les gens ont l'intention de décrire quelque chose comme impliquant un changement énorme qui se produit sur une courte période de temps. Le terme s'applique en fait à la façon dont un électron se comporte dans un atome, soit lorsqu'il absorbe un photon venant de l'extérieur et saute donc d'une orbite autour du noyau de l'atome à une orbite plus élevée, soit lorsqu'il émet un photon et tombe donc d'une orbite plus élevée à une orbite plus basse. L'idée de Neils Bohr et de ses collègues était que l'électron ne se déplace pas d'une orbite à l'autre mais qu'au contraire il disparaît d'une orbite et apparaît instantanément dans une autre orbite. Ainsi, un saut quantique n'est pas vraiment un changement de la Terre, mais un petit changement soudain d'un domaine à un autre.

Lorsque les humains mesurent un processus à l'échelle subatomique et que le principe d'incertitude se manifeste, on peut dire que l'action humaine a influencé la chose qui était mesurée. Faire une mesure destinée à obtenir une indication précise de la position d'une particule influencera inévitablement son élan et quoi que l'on fasse pour mesurer cet élan le plus tôt possible après avoir mesuré sa position, les probabilités de découvrir l'élan ne peuvent manquer d'être modifiées. Le principe d'incertitude peut donc expliquer certains types d'interférences produites par les chercheurs qui influencent les résultats d'une expérience ou d'une observation. Cependant, tous les effets des observateurs ne sont pas dus à des effets quantiques ou au principe d'incertitude. Les autres sont des "effets d'observation" mais pas des effets d'incertitude quantique.

Les effets d'observation comprennent toutes sortes de choses qui fonctionnent à l'échelle humaine ordinaire des événements. Si un anthropologue tente de se faire une idée précise de la vie dans une société primitive mais que sa présence dérange la communauté qu'il visite, les observations faites peuvent être très trompeuses. Cependant, aucune des interactions pertinentes ne se produit au niveau décrit par la mécanique quantique ou le principe d'incertitude.

Parfois, le mot "quantum" sera utilisé à des fins publicitaires pour indiquer quelque chose de nouveau et de puissant. Par exemple, le fabricant de petits moteurs à essence, Briggs and Stratton, propose une gamme de moteurs quatre cylindres de faible puissance pour tondeuses à essence et outils de jardin similaires qu'il appelle "Quantum".

Plus de lecture

• Introduction à la théorie quantique, p. 115 et p. 158

J.P. McEvoy et Oscar Zarate