Trigonométrie

Vue d'ensemble et définitions

La trigonométrie utilise un grand nombre de mots spécifiques pour décrire les parties d'un triangle. Voici quelques-unes des définitions de la trigonométrie :

• Triangle à angle droit - Un triangle à angle droit est un triangle dont l'angle est égal à 90 degrés. (Un triangle ne peut pas avoir plus d'un angle droit) Les rapports trigonométriques standard ne peuvent être utilisés que pour les triangles à angle droit.
• Hypoténuse - L'hypoténuse d'un triangle est le côté le plus long, et le côté opposé à l'angle droit. Par exemple, pour le triangle de droite, l'hypoténuse est le côté c.
• Opposé d'un angle - Le côté opposé d'un angle est le côté qui ne coupe pas le sommet de l'angle. Par exemple, le côté a est l'opposé de l'angle A dans le triangle à droite.
• Adjacent d'un angle - Le côté adjacent d'un angle est le côté qui coupe le sommet de l'angle mais qui n'est pas l'hypoténuse. Par exemple, le côté b est adjacent à l'angle A dans le triangle de droite.

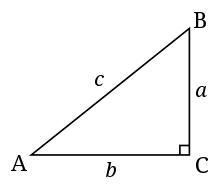
Un triangle droit standard. C est l'angle droit dans cette image

Ratios trigonométriques

Il existe trois principaux rapports trigonométriques pour les triangles droits, et trois réciproques de ces rapports. Il y a 6 ratios totaux. Ils sont :

• Sinus (sinus) - Le sinus d'un angle est égal à l'hypoténuse opposée {{\text{Opposite}} \over {\text{Hypotenuse}}}
• Cosinus (cos) - Le cosinus d'un angle est égal à l'hypoténuse adjacente \over {\text{Hypotenuse}}}
• Tangente (tan) - La tangente d'un angle est égale au style d'affichage de la partie adjacente opposée {{\text{Opposite}} \over {\text{Adjacent}}}

Les réciproques de ces ratios sont :

Cosécante (csc) - La cosécante d'un angle est égale à l'hypoténuse opposée {{\text{Hypoténuse}} \over {\text{Opposite}}}} ou csc θ = 1 sin θ {\displaystyle \csc \theta ={1 \over \sin \theta}}

Sécante (sec) - La sécante d'un angle est égale à l'hypoténuse adjacente {{\text{Hypoténuse}} \over {\text{Adjacent}}}} ou sec θ = 1 cos θ {\displaystyle \sec \theta ={1 \over \cos \theta}}

Cotangente (cot) - La cotangente d'un angle est égale à la cotangente du style d'affichage "Adjacent Opposé" {{\text{Adjacent}} \over {\text{Opposite}}}} or cot θ = 1 tan θ {\displaystyle \cot \theta ={1 \over \tan \theta}}

Les étudiants utilisent souvent un moyen mnémotechnique pour se souvenir de cette relation. Les rapports sinus, cosinus et tangents dans un triangle rectangle peuvent être mémorisés en les représentant sous forme de chaînes de lettres, comme SOH-CAH-TOA :

Sinus = Opposé ÷ Hypoténuse

Cosinus = Adjacent ÷ Hypoténuse

Tangente = Opposé ÷ Adjacent

Utilisation de la trigonométrie

Avec les sinus et les cosinus, on peut répondre à pratiquement toutes les questions sur les triangles. C'est ce qu'on appelle "résoudre" le triangle. On peut calculer les angles et les côtés restants de n'importe quel triangle dès que l'on connaît deux côtés et leur angle inclus ou deux angles et un côté ou trois côtés. Ces lois sont utiles dans toutes les branches de la géométrie, puisque chaque polygone peut être décrit comme une combinaison de triangles.

La trigonométrie est également essentielle dans le domaine de la topographie, de l'analyse vectorielle et de l'étude des fonctions périodiques.

Il existe aussi la trigonométrie sphérique, qui traite de la géométrie sphérique. Elle est utilisée pour les calculs en astronomie, en géodésie et en navigation.

Lois sur la trigonométrie

Loi des sinus

a Sin A = b Sin B = c Sin C {{\text{a}} \over {\text{Sin A}}}={{\text{b}} \over {\text{Sin B}}}={{\text{c}} \over {\text{Sin C}}}}

Loi de Cosines

a 2 = b 2 + c 2 - 2 b c cos ( A ) {\displaystyle a^{2}=b^{2}+c^{2}-2bc\cos(A)}

La loi des tangentes

a - b a + b = tan ( 1 2 ( A - B ) ) tan ( 1 2 ( A + B ) ) {\displaystyle {\frac {a-b}{a+b}}={\frac {\tan({\frac {1}{2}}(A-B))}{\tan({\frac {1}{2}}(A+B))}}}