Fonction trigonométrique
En mathématiques, les fonctions trigonométriques sont un ensemble de fonctions qui relient les angles aux côtés d'un triangle rectangle. Il existe de nombreuses fonctions trigonométriques, les 3 plus courantes étant le sinus, le cosinus, la tangente, suivie de la cotangente, de la sécante et de la cosécante. Les trois dernières sont appelées fonctions trigonométriques réciproques car elles agissent comme les réciproques d'autres fonctions. La sécante et la cosécante sont rarement utilisées.
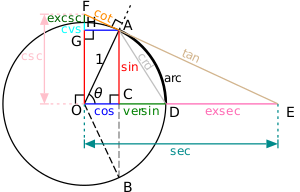
Toutes les fonctions trigonométriques d'un angle quelconque peuvent être construites à l'aide d'un cercle centré sur O et de rayon 1.

Fonctions trigonométriques : Sinus , Cosinus , Tangente , Cosécante, Sécante , Cotangente
Définition
Les fonctions trigonométriques sont parfois aussi appelées fonctions circulaires. Ce sont des fonctions d'un angle ; elles sont importantes pour l'étude des triangles, parmi de nombreuses autres applications. Les fonctions trigonométriques sont communément définies comme les rapports des deux côtés d'un triangle rectangle contenant l'angle, et peuvent être définies de façon équivalente comme les longueurs de divers segments de ligne d'un cercle unitaire (un cercle qui a un rayon de un).
Définitions des triangles droits
Afin de définir les fonctions trigonométriques pour l'angle A, commencez par un triangle rectangle qui contient l'angle A :
Nous utilisons les noms suivants pour les côtés du triangle :
- L'hypoténuse est le côté opposé à l'angle droit, ou défini comme le côté le plus long d'un triangle rectangle, dans ce cas h.
- Le côté opposé est le côté opposé à l'angle qui nous intéresse, dans ce cas a.
- Le côté adjacent est le côté qui est en contact avec l'angle qui nous intéresse et l'angle droit, d'où son nom. Dans ce cas, le côté adjacent est b.
Tous les triangles sont considérés comme existant en géométrie euclidienne, de sorte que les angles intérieurs de chaque triangle s'additionnent à π radians (ou 180°) ; par conséquent, pour un triangle droit, les deux angles non droits sont compris entre zéro et π/2 radians. Le lecteur doit noter que les définitions suivantes, à proprement parler, ne définissent que les fonctions trigonométriques pour les angles situés dans cette plage. Nous les étendons à l'ensemble des arguments réels en utilisant le cercle unitaire, ou en exigeant certaines symétries et qu'il s'agisse de fonctions périodiques.
1) Le sinus d'un angle est le rapport entre la longueur du côté opposé et la longueur de l'hypoténuse. Dans notre cas
sin A = hypoténuse opposée = a h . {\displaystyle \sin A={\frac {opposite}}{\textrm {hypotenuse}}={\frac {a}{h}}. }
Notez que ce rapport ne dépend pas du triangle droit choisi, tant qu'il contient l'angle A, car tous ces triangles sont similaires.
L'ensemble des zéros du sinus (c'est-à-dire les valeurs de x pour lesquelles le sinus x

{ n π | n ∈ Z } . {\displaystyle \left\{n\pi {\big |}n\in \mathbb {Z} \D'accord.} }
2) Le cosinus d'un angle est le rapport entre la longueur du côté adjacent et la longueur de l'hypoténuse. Dans notre cas
cos A = hypoténuse adjacente = b h . {\displaystyle \cos A={\frac{\frac {adjacent}}{\textrm {hypotenuse}}}={\frac{\b}{h}}. }
L'ensemble des zéros du cosinus est
{ π 2 + n π | n ∈ Z } . {\displaystyle \left\{{\frac {\pi }{2}}+n\pi {\bigg |}n\in \mathbb {Z} \D'accord.} }
3) La tangente d'un angle est le rapport entre la longueur du côté opposé et la longueur du côté adjacent. Dans notre cas, la tangente
tan A = opposé adjacent = a b . {\displaystyle \tan A={\frac {opposite}}{\textrm {adjacent}}={\frac {a}{b}}. }
L'ensemble des zéros de la tangente est
{ n π | n ∈ Z } . {\displaystyle \left\{n\pi {\big |}n\in \mathbb {Z} \D'accord.} }
Le même ensemble de la fonction sinusoïdale depuis
tan A = sin A cos A . {\displaystyle \tan A={\frac{\sin A}{\cos A}}. }
Les trois fonctions restantes sont mieux définies en utilisant les trois fonctions ci-dessus.
4) La cosécante csc(A) est l'inverse multiplicatif de sin(A), c'est-à-dire le rapport entre la longueur de l'hypoténuse et la longueur du côté opposé :
csc A = hypoténuse opposée = h a {\displaystyle \csc A={\frac {\textrm {hypoténuse}}{\textrm {opposite}}}={\frac {h}{a}}}
5) Le secant sec(A) est l'inverse multiplicatif de cos(A), c'est-à-dire le rapport de la longueur de l'hypoténuse à la longueur du côté adjacent :
sec A = hypoténuse adjacente = h b {\displaystyle \sec A={\frac {\textrm {hypoténuse}}{\textrm {adjacent}}}={\frac {h}{b}}}
6) Le cotangente cot(A) est l'inverse multiplicatif de tan(A), c'est-à-dire le rapport de la longueur du côté adjacent à la longueur du côté opposé :
cot A = adjacent opposé = b a {\displaystyle \cot A={\frac {\textrm {adjacent}}{\textrm {opposite}}}={\frac {b}{a}}}
Définitions par série de puissance
On peut aussi définir les fonctions trigonométriques en utilisant des séries de puissance :
sin x = x - x 3 3 ! + x 5 5 ! - − x 7 7 ! + ⋯ = ∑ n = 0 ∞ ( - 1 ) n x 2 n + 1 ( 2 n + 1 ) ! {\displaystyle \sin x=x-{\frac {x^{3}{3!}}+{\frac {x^{5}{5!}}-{\frac {x^{7}{7!}}+\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n+1}}{(2n+1)!}}}
cos x = 1 - x 2 2 ! + x 4 4 ! - − x 6 6 ! + ⋯ = ∑ n = 0 ∞ ( - 1 ) n x 2 n ( 2 n ) ! {\displaystyle \cos x=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}{4!}}-{\frac {x^{6}{6!}}+\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n}}{(2n)!}}}
et définir la tangente, la cotangente, la sécante et la cosécante en utilisant des identités, voir ci-dessous.
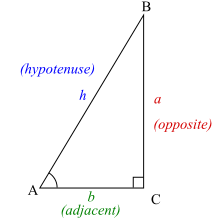
Un triangle rectangle comprend toujours un angle de 90° (π/2 radians), ici appelé C. Les angles A et B peuvent varier. Les fonctions trigonométriques spécifient les relations entre les longueurs des côtés et les angles intérieurs d'un triangle rectangle.
Identités
Quelques identités importantes :
tan x = sin x cos x {\displaystyle \tan x={\frac {\sin x}{\cos x}}}
cot x = cos x sin x {\displaystyle \cot x={\frac {\cos x}{\sin x}}}
sec x = 1 cos x {\displaystyle \sec x={\frac {1}{\cos x}}}
csc x = 1 sin x {\displaystyle \csc x={\frac {1}{\sin x}}}
sin 2 x + cos 2 x = 1 {\displaystyle \sin ^{2}x+\cos ^{2}x=1}
sin 2 x = 2 sin x cos x {\displaystyle \sin 2x=2\sin x\cos x}
cos 2 x = cos x cos x - sin x sin x = cos 2 x - sin 2 x = 2 cos 2 x - 1 = 1 - 2 sin 2 x {\displaystyle \cos 2x=\cos x\cos x-\sin x\sin x=\cos ^{2}x-\sin ^{2}x=2\cos ^{2}x-1=1-2\sin ^{2}x}
tan 2 x = 2 tan x 1 - tan 2 x {\displaystyle \tan 2x={\frac {2\tan x}{1-\tan ^{2}x}}}
sin ( x ± y ) = sin x cos y ± cos x sin y {\displaystyle \sin \left(x\pm y\right)=\sin x\cos y\pm \cos x\sin y}
cos ( x ± y ) = cos x cos y ∓ sans x sans y {displaystyle }cos \left(x\pm y\right)=cos x\cos y\mp sans x\sin y
tan ( x ± y ) = tan x ± tan y 1 ∓ tan x tan y {\displaystyle \tan \left(x\pm y\right)={\frac {\tan x\pm \tan y}{1\mp \tan x\tan y}}}
Fonctions hyperboliques
Les fonctions hyperboliques sont comme les fonctions trigonométriques en ce sens qu'elles ont des propriétés très similaires. Elles sont définies en termes de fonction exponentielle, qui est basée sur la constante e.
- Le sinus hyperbolique :
sinh x = e x - e - x 2 = e 2 x - 1 2 e x = 1 - e - 2 x 2 e - x . {\displaystyle \sinh x={\frac {e^{x}-e^{-x}}{2}}={\frac {e^{2x}-1}{2e^{x}}}={\frac {1-e^{-2x}}{2e^{-x}}}. }
- Le cosinus hyperbolique :
cosh x = e x + e - x 2 = e 2 x + 1 2 e x = 1 + e - 2 x 2 e - x . {\displaystyle \cosh x={\frac {e^{x}+e^{-x}}{2}}={\frac {e^{2x}+1}{2e^{x}}}={\frac {1+e^{-2x}}{2e^{-x}}}. }
- Tangente hyperbolique :
tanh x = sinh x cosh x = e x - e - x e x + e - x = e 2 x - 1 e 2 x + 1 = 1 - e - 2 x 1 + e - 2 x . {\displaystyle \tanh x={\frac {sinh x}{\cosh x}}={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}}={\frac {e^{2x}-1}{e^{2x}+1}}}={\frac {1-e^{-2x}}{1+e^{-2x}}}. }
- Cotangente hyperbolique :
coth x = cosh x sinh x = e x + e - x e x - e - x = e 2 x + 1 e 2 x - 1 = 1 + e - 2 x 1 - e - 2 x , x ≠ 0. {\displaystyle \coth x={\frac {cosh x}{\sinh x}}={\frac {e^{x}+e^{-x}}{e^{x}-e^{-x}}}}={\frac {e^{2x}+1}{e^{2x}-1}}={\frac {1+e^{-2x}}{1-e^{-2x}}},\qquad x\neq 0.}
- Sécante hyperbolique :
sech x = 1 cosh x = 2 et x + e - x = 2 et x et 2 x + 1 = 2 et - x 1 + e - 2 x . (sech.) {\,x={\frac {cosh x}}}{\frac {\2}{x}+e^{-x}}}={\frac {\2e^x}}{2x}+1}={\frac {2e^{-x}}{1+e^{-2x}}}. }
- Cosécante hyperbolique :
csch x = 1 sinh x = 2 e x - e - x = 2 e x e 2 x - 1 = 2 e - x 1 - e - 2 x , x ≠ 0. {\displaystyle \operatorname {csch} \,x={\frac {1}{\sinh x}}={\frac {2}{e^{x}-e^{-x}}}={\frac {2e^{x}}{e^{2x}-1}}={\frac {2e^{-x}}{1-e^{-2x}}},\qquad x\neq 0.}
Pages connexes
- Le théorème de Pythagore
- Trigonométrie
Rechercher dans l'encyclopédie
























